Файл: Informatika2013-Of2010.doc

Получение математической модели одномерного объекта

Для определения математической модели некоторого объекта нужно провести эксперимент и получить табличную зависимость значений выходного параметра процесса y от значений входного параметра x. Затем для выбранного вида математической модели, которую в общем виде можно записать y = f(x, a0, a1, a2, …, am), определяются значения параметров a0, a1, …, am, которые обеспечивают соответствие этой модели экспериментальным данным.

В соответствии с методом наименьших квадратов параметры a0, a1, …,am выбираются так, чтобы была минимальной сумма квадратов:

Чтобы найти нужные параметры, следует взять частные производные от правой части по a0, a1, …, am и приравнять их к нулю. Полученную систему уравнений можно решить одним из известных методов.

Например, для полинома второй степени y = a0 + a1x + a2x² искомые значения a0, a1, a2 определяются решением системы линейных уравнений:

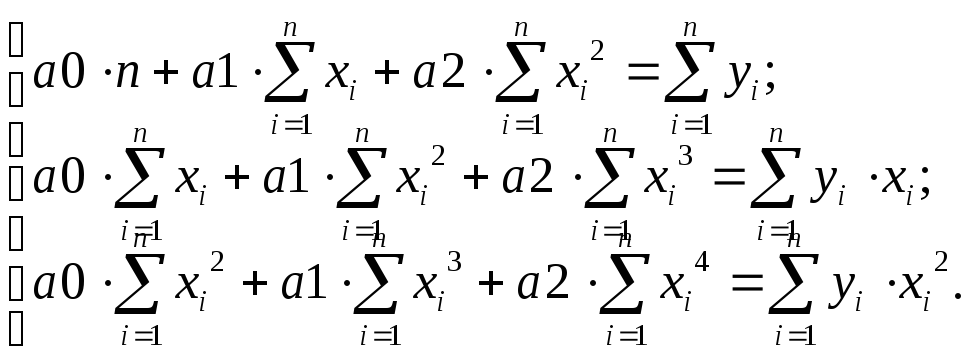
Рассмотрим алгоритм метода наименьших квадратов для вычисления коэффициентов полинома второй степени:

1. Ввод количества опытов n, значений x₁, x₂, …, x_n, y₁, y₂, …, y_n.

2. Определение коэффициентов системы линейных уравнений:

a_1,2 = a_1,3 = a_2,3 = a_3,3 = b₁ = b₂ = b₃ =

a_1,1 = n, a_2,1 = a_1,2, a_2,2 = a_1,3, a_3,1 = a_1,3, a_3,2 = a_2,3.

3. Решение системы AZ = B, где A – матрица коэффициентов; Z – вектор, в котором определяются корни z₁ = a0, z₂ = a1, z₃ = a2; B – вектор свободных членов системы.

4. Вывод искомых коэффициентов a0, a1, a2.

5. Определение и вывод разностей (так называемых невязок) ₁, ₂, …, _n.

Рассмотрим пример, в котором определяется система уравнений для вычисления параметров a, b, c математической модели y = acos(x) + bln(x) + c.

Частные производные:

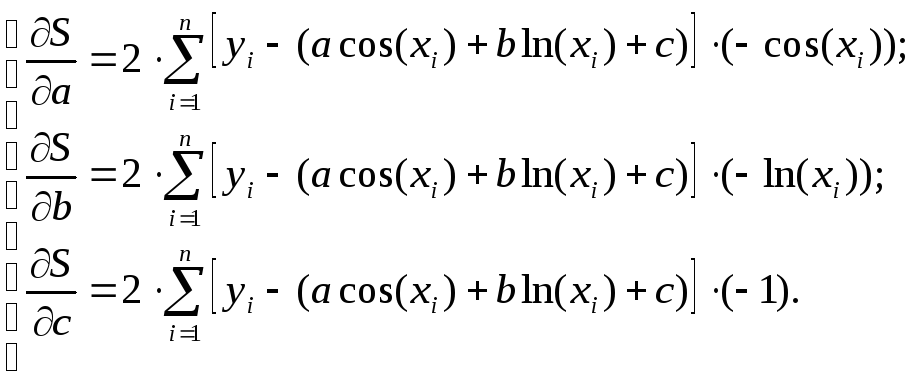
Таким образом, система линейных уравнений для определения параметров модели y = acos(x) + bln(x) + c принимает вид:

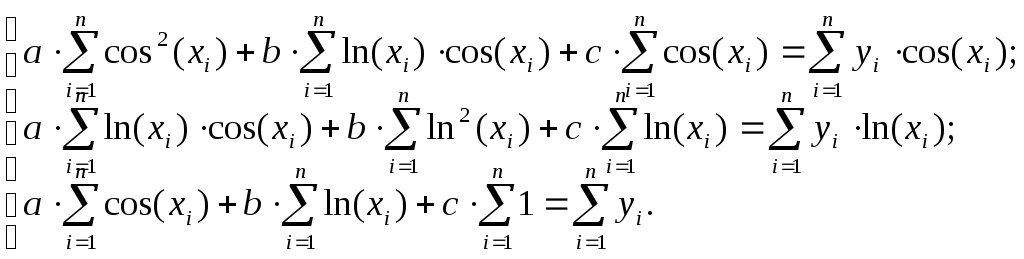
Получение математических моделей одномерных объектов в приложении Excel. В приложении Excel имеется возможность получения математических моделей через построение графиков функций. Пусть имеются значения x₁, x₂, …, x_n и соответствующие им значения y₁, y₂, …, y_n. Надо для этих данных построить точечный график и выполнить Работа с диаграммами / Макеты диаграмм / Добавить элемент диаграммы / Линия тренда / Дополнительные параметры линии тренда.

В появившемся окне на вкладке определить вид математической модели и отметить флажок Показывать уравнение на диаграмме. После нажатия ОK искомое уравнение появится на графике.

Получение математических моделей одномерных объектов в приложении Mathcad. В приложении Mathcad можно записать формулы приведенного выше алгоритма и вычислить коэффициенты функциональной зависимости. Существуют также и встроенные функции для определения математических моделей.

Например, пусть имеются значения х и у, полученные в результате проведения опытов. Надо найти математическую модель в виде полинома второй степени: y = a0 + a1 x + a2 x²

Можно использовать для решения задачи встроенную функцию linfit. На листе Mathcad тогда нужно записать:

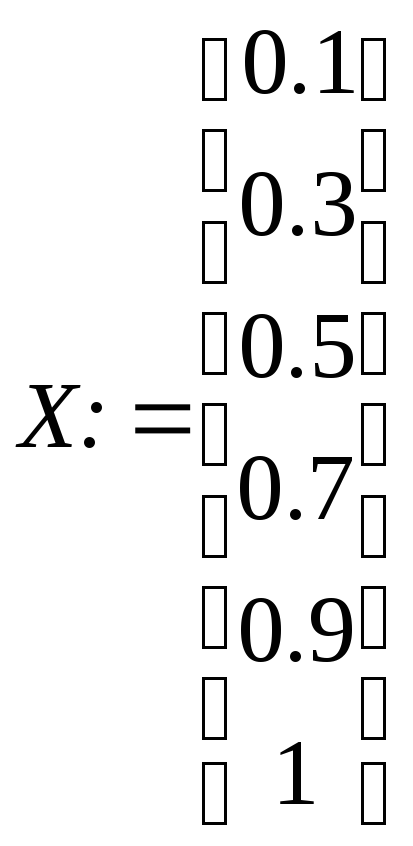
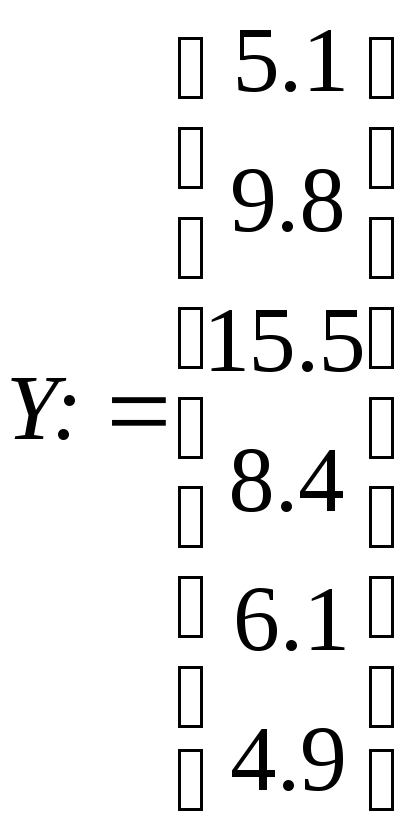
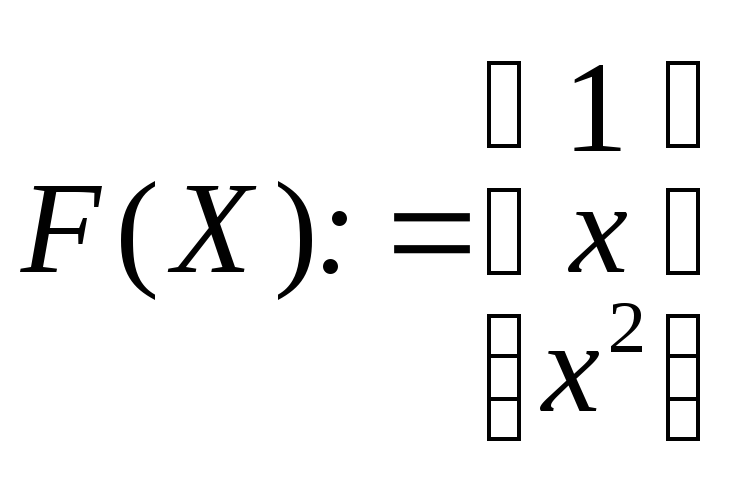
А:= linfit(Х,Y,F)

Вычисленные значения a0, a1, a2 будут записаны в векторе А, который появится после ввода: A =

Для построения графика теперь можно определить значения:

i:= 0..5 t:= 0, 0.01..1 Z(t):= F(t)*A

Здесь Z(t) − искомая математическая модель.

Если построить на одном графике зависимость Z(t) от t и зависимость Y_i от X_i, то можно сравнить, насколько хорошо полученный полином описывает данные опытов.

Назад

Решение задач оптимизации

Способы использования компьютера для решения задач оптимизации рассмотрим на примере.

Пусть имеется объект с двумя входными параметрами x1, x2 и выходным параметром y. Требуется определить оптимальные значения x1 и x2, которые обеспечивают минимум целевой функции y = f(x1, x2) и удовлетворяют ограничениям:

a1 <= x1<= b1, a2 <= x2<= b2, g(x1, x2) > 0.

Метод сканирования заключается в нахождении значений x1 из интервала [a1, b1] с шагом h1 и значений x2 из интервала [a2, b2] с шагом h2. Для всех значений x1 и x2, удовлетворяющих ограничениям g(x1, x2)>0, нужно вычислить значения целевой функции y = f(x1, x2). Те x1 и x2, для которых значение целевой функции минимально, являются решением задачи.

Здесь А – число, заведомо большее, чем значения целевой функции при определении минимума, и заведомо меньшее, чем значения целевой функции при определении максимума. Необходимо также написать две функции пользователя, в которых вычисляются целевая функция и ограничение.

Функция пользователя для вычисления целевой функции	Функция пользователя для вычисления ограничения (если оно присутствует)
Function F(X1, X2) F = End Function	Function G(X1, X2) G = End Function

Метод случайного поиска рассмотрим на том же примере. Идея метода основана на многократном (N раз) вычислении целевой функции y для значений x1 и x2, выбранных из отрезков [a1, b1] и [a2, b2] случайным образом. Те значения x1 и x2, при которых целевая функция минимальна и удовлетворяются ограничения, являются решением задачи.

Для определения некоторого случайного числа x на отрезке [a, b] можно использовать встроенную функцию Rnd. Тогда x = (b – a)Rnd(1) + a.

Алгоритм метода случайного поиска

1. Ввод исходных данных: a1, b1, a2, b2, количества опытов N и числа A, заведомо большего, чем значение целевой функции.

2. Вычисление yopt = A, x1opt = a1, x2opt = a2.

3. i = 1.

4. Вычисление x1 = (b1 – a1) Rnd(1) + a1, x2 = (b2 – a2) Rnd(1) + a2.

5. Проверка ограничения: если g(x1, x2) <= 0 , то переход к пункту 8, иначе – переход к следующему пункту.

6. Вычисление целевой функции y = f(x1, x2).

7. Если y < yopt, то yopt = y, x1opt = x1, x2opt = x2, иначе – переход к следующему пункту.

8. i = i + 1.

9. Если i <= N, то переход к пункту 4, иначе – переход к пункту 10.

10. Вывод оптимальных значений x1opt, x2opt и минимального значения целевой функции yopt.

Решение задач оптимизации в приложении Excel. В приложении Excel имеется специальная команда, с помощью которой можно решать задачи оптимизации. Например, чтобы решить предыдущий пример, следует произвести следующие действия