Файл: Гагин. Системный синтез. Линия жизни.doc

Накопленные знания, об этом уникальном соотношении частей в целом, по эстафете передаются из поколения в поколение, наполняясь новым содержанием, обнаруживаются в самых разнообразных явлениях, используются практически во всех областях науки, проникают в технику.

Такая универсальность Золотой Пропорции, не делает её простой и доступной для изучения. Многое, в сущности этой «константы гармоничности», остаётся загадочным. Ещё неясно, почему Природа предпочла эту пропорцию всем другим, – не за её ли уникальность?

Характерно, что ЗП отвечает делению целого на две неравные части. Следовательно, она отвечает асимметрии. Почему же она так привлекательна? Даже больше, чем симметрические пропорции. Очевидно, эта пропорция обладает каким-то особым, уникальным свойством.

Целое можно поделить на бесконечное множество неравных частей. Но, только одно из таких сечений отвечает ЗП. По-видимому, в этой пропорции скрыта одна из фундаментальных тайн Природы, которую ещё предстоит открыть и исследовать. Отрезок прямой АВ можно разделить на две части следующими способами:

• на две равные части – АВ : АС = АВ : ВС;

• на две неравные части в любом отношении (такие части пропорции не образуют);

• таким образом, когда АВ : АС = АС : ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

a : b = b : c или с : b = b : а.

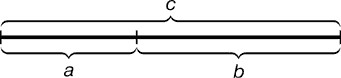
Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

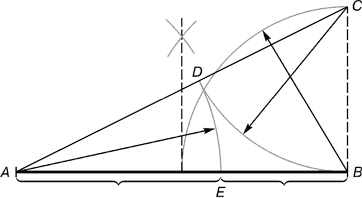
Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Золотое сечение – понятие математическое. Его изучение это, прежде всего, задача науки. Но, оно же, является критерием гармонии, красоты и совершенства. А это уже категории философские и религиозные, интуитивные и эстетические.

Остановимся на феномене Золотой Пропорции подробнее.

Сегодня трудно установить достоверно: кто и когда впервые открыл для человечества Золотую Пропорцию. Очевидно, её открывали и забывали неоднократно. Но, многие исследователи, считают её первооткрывателем, греческого математика и философа Пифагора.

Рассмотрим свойства Золотой Пропорции. Возьмём, для иллюстрации, простой прямоугольный треугольник с отношением сторон (катетов) 1: 2. В этом треугольнике величина малого катета равна 1, а большого 2. По теореме Пифагора, длина гипотенузы будет равна Ö 5 . Эта величина могла положить начало открытию несоизмеримых или иррациональных чисел.

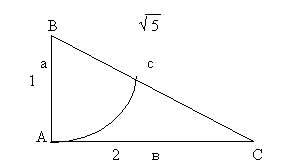
Соотношения сторон данного треугольника (а, в, с) простые:

__ __

а/в = 1/2 с/а = Ö 5 /1 с/в = Ö 5 /2

Из этих величин следует ещё одно отношение:

___

(а + с) : в = (1 + Ö 5 ) : 2 = 1,618033…

Это и есть Золотая Пропорция, которую обозначают через Ф, по имени Фидия (начало 5 века до н. э.), древнегреческого скульптора, периода высокой классики. Его творчество, в котором широко использована Золотая Пропорция, одно из высших достижений мирового искусства.

1/Ф = 0,618033…

Число Ф – единственное положительное число, которое переходит в обратное ему при вычитании единицы.

Его, также можно представить:

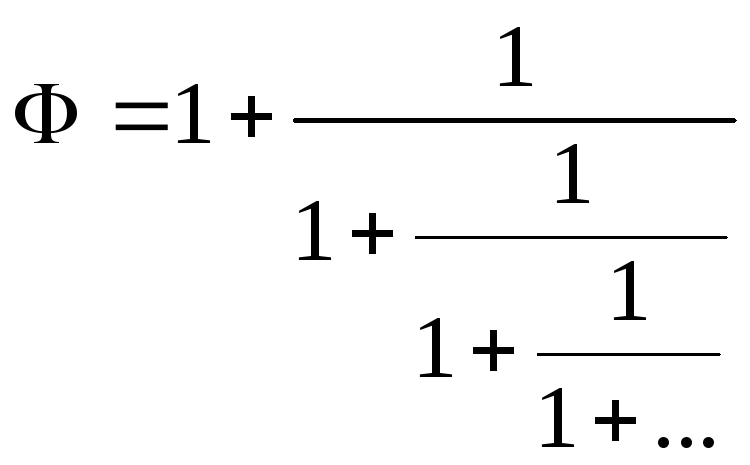
или:

Если в прямоугольнике, со сторонами 1:2, провести диагональ и описать полуокружность, радиусом равным диагонали, то получим фигуру, в которой содержаться интересные пропорции. Отношения этой фигуры содержат пропорции египетских пирамид, греческого храма Парфенона, размерностей русских саженей, римского пасса и Золотой пропорции.

Египетские пирамиды – грандиозные сооружения древности. Поэтому, маловероятно, что их формы и размеры выбраны произвольно. Исследования говорят, что каждая деталь, каждый элемент пирамиды, выбирались тщательно и должны были продемонстрировать высокий уровень знаний создателей пирамид, как представителей развитой цивилизации.

Сегодня есть все основания утверждать, что основным отношением частей пирамид является Золотая Пропорция, выраженная неоднократно, и число «p». Следует только удивляться высокому знанию и искусству древних математиков и архитекторов Египта, которые смогли воплотить в пирамидах две иррациональные (несоизмеримые) величины – «p» и Ф со столь поразительной точностью.

Учёные ищут разгадку секретов знаменитой пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скоpее, неразрешимая головоломка из числовых комбинаций. Замечательная изобретательность, мастерство, время и труд архитекторов пирамиды, использованные ими пpи возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической, и символы были единственным средством передать информацию.

По преданиям, ключ к секрету пирамиды в Гизе, был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.

Площадь треугольника:

356 x 440 / 2 = 78320

Площадь квадрата:

280 x 280 = 78400

Длина грани пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды - 484.4 фута (147.6 м). Длина грани, делённая на высоту, приводит к соотношению:

Ф = 1,618

Высота 484.4 фута соответствует 5813 дюймам (5-8-13) - это числа из последовательности Фибоначчи.

Наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618. Современные ученые склоняются к мысли, что древние египтяне построили ее с единственной целью - передать знания, которые они хотели сохранить для грядущих поколений.

Исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет определяющую роль.

Аналогичные закономерности в строительстве обнаружены и у мексиканских пирамид. Напрашивается мысль, что как египетские, так и мексиканские пирамиды возводились примерно в одно и то же время, цивилизациями, имевшими общие корни.

На поперечном сечении пирамиды видна конструкция, подобная лестнице. В первом ярусе 16 ступеней, во втором - 42 ступени и в третьем - 68 ступеней.

Эти числа связаны с рядом Фибоначчи:

16 x 1.618 = 26

16 + 26 = 42

26 x 1.618 = 42

42 + 26 = 68

И так далее.

У исследователей ещё непочатый край работы.

1.2.6.2. Рекуррентный, аддитивный ряд чисел фибоначчи – ключ к гармонии мира

«Искусство – завуалированная алгебра, отнимающая жизнь у тех, кто стремится приподнять её покрывало».

(Бурдель)

Итальянский математик Леонардо Фибоначчи нашёл ряд натуральных чисел:

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

в котором, каждое последующее число – сумма двух предыдущих:

^V₁ ^{, V}₂ ^{, … V} _п

^{где, V} _п^{= V} _п-1^{+ V}_п-2 т. е. , рекуррентный ряд.

В математике, рекуррентный ряд – это ряд чисел возвратной последовательности, т. е., каждый следующий член ряда, начиная с некоторого, выражается по определённому правилу, через предыдущий. Аддитивный, значит полученный путём сложения.

Немного истории. Итальянский купецЛеонардо из Пизы (1180-1240), более известен под прозвищем Фибоначчи. Он был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.

Жизнь и научная карьера Леонардо теснейшим образом связана с развитием европейской культуры и науки.

В век Фибоначчи, до Возрождения было еще далеко, однако история даровала Италии краткий промежуток времени, который вполне можно было назвать репетицией надвигающейся эпохи Ренессанса. Этой репетицией руководил Фридрих II, император Священной Римской империи. Воспитанный в традициях южной Италии,этот правитель был, внутренне далек от европейского христианского рыцарства.

Столь любимые его дедом рыцарские турниры, Фридрих II совсем не признавал. Вместо этого он культивировал, гораздо менее кровавые, математические соревнования, на которых, противники обменивались не ударами, а задачами.

На таких турнирах и заблистал талант Леонардо Фибоначчи. Этому способствовало хорошее образование, которое дал сыну купецБоначчи, взявший его с собой на Восток и приставивший к нему арабских учителей.

Покровительство Фридриха и стимулировало выпуск научных трактатов Фибоначчи:

• «Книга абака», написанная в 1202 году, но дошедшая до нас во втором своем варианте, который относится к 1228 г.

• «Практики геометрии» (1220г.)

• «Книга квадратов» (1225г.)