Файл: Г.М. Гринфельд лекции по курсу дискретные системы автоматического управления.doc

Каждому из них соответствует одно из трех слагаемых в выражении . Для определения первых двух может быть использована формула (64). При этом, вычисляя первое слагаемое модифицированной решетчатой функции,следует считать равным, а при вычислении второго слагаемого. Третье слагаемоене имеет нулевого корня, поэтому при вычислении третьей составляющейполагаем, но параметрв (64) заменяем на. При вычислении всех трех слагаемых в выражениисчитаем, что

.

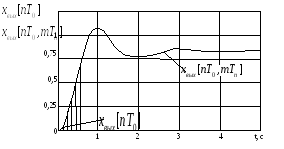
Рис. 55 Графики функций и

нескорректированной дискретной САУ

Для произвольных моментов времени величина выходного сигнала рассматриваемой системы равна:

Здесь .

На рис. 55 приведены графики функций и.

3. Построение логарифмических амплитудно- и фазочастотных характеристик (ЛАХ и ФЧХ) дискретных систем выполняется в функции абсолютной псевдо частоты , связанной с частотойследующей зависимостью:

Переход к частотным характеристикам производится в два этапа. Первоначально необходимо вычислить передаточную функцию , для чего в передаточной функции нескорректированной системыпеременнаяполагается равной:

Затем в полученном выражении делается замена.

Построение асимптотической ЛАХ по видупроизводится по тем же правилам, что и для непрерывных систем. При построении ФЧХследует обращать внимание на наличие неминимально - фазового сомножителяв числители функции. Определяемая им составляющаяравна:

Для рассматриваемой системы:

;

ЛАХ и ФЧХ нескорректированной разомкнутой системы приведены на рис. 56.

3. Один из возможных способов коррекции дискретных САУ основывается на использовании аналогового корректирующего звена, включенного последовательно в непрерывную часть системы, как показано на рис. 57. При этом передаточная функция разомкнутой скорректированной системы равна:

(65)

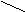
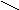
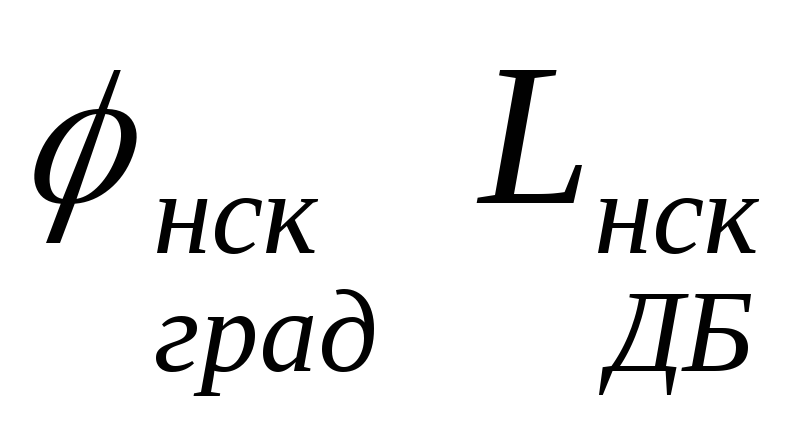
Рис. 56Логарифмические частотные характеристики

нескорректированной дискретной САУ

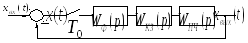
Рис. 57 Структурная схема дискретной САУ с последовательным

аналоговым корректирующим звеном

Для нахождения передаточной функции предварительно необходимо определить желаемую передаточную функцию. С этой целью сначала строится желаемая ЛАХ разомкнутой скорректированной системы. Построениеосуществляется по методикам, разработанным для непрерывных САУ, с учетом всех требований, предъявляемых к дискретной системе. Для рассматриваемого примера вид желаемых характеристикиприведен на рис. 58. Частотная характеристика дискретной САУ с фиксатором обязательно имеет в числителе сомножитель, поэтому выбранной желаемой ЛАХ соответствуют следующие выражения дляи:

,

90 20 0 0 -90 -20 -180 -40 -270 -60 20 2 1

Рис. 58Логарифмические частотные характеристики дискретной

САУ с последовательным аналоговым корректирующим звеном

Запас по фазе в скорректированной системе составляет .

От осуществляется переход к передаточной функции, для чего используется подстановка. Далее, полагая, преобразует передаточную функциюк выражению для.

Для рассматриваемой системы:

;

Если передаточная функция определена, то на основании (65) можно найти выражение, являющееся- изображением функции:

.

Затем следует определить , для чего необходимо выполнить операцию обратного- преобразования:

(66)

Проще всего такое преобразование выполняется, если функция включена в таблицу- преобразований. В противном случае можно разложитьна простые слагаемые, для каждого из которых функция-оригинал находится по таблице. Другой путь выполнения обратного- преобразования заключается в следующем: поопределяется решетчатая функция, которая с помощью подстановкипреобразуется в непрерывную функцию; затем осуществляется преобразование Лапласа функции, в результате чего определяется искомое выражение.