Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4597
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
2.Решите уравнение :
3.Найдите наибольшее целое число – решения неравенства
.4. Решить неравенство
3 ВАРИАНТ
1.Пусть х0-корень уравнения 4х+2 − 3⋅4х=208. Найти значение выражения 3х0-1.
2. Решите уравнение :
.3. Найдите наименьшее целое число -решения неравенства
.4. Решить неравенство
4 ВАРИАНТ.
1.Пусть х0-корень уравнения 5х+3 − 10⋅5х=23. Найти значение выражения 5х0+4.
2.Решите уравнение :
.3.Найдите наибольшее целое число – решения неравенства
.4. Решить неравенство
.| Критерий оценивания | № задания | Дескриптор | Балл | |
| Обучающийся | ||||
| Решает показательное уравнение | 1 | упрощает выражение, применяя свойства степени; | 1 | |
| применяет метод решения однородного уравнения; | 1 | |||
| находит корни уравнения; | 1 | |||
| находит значение выражения; | 1 | |||
| Решает логарифмическое уравнение | 2 | находит область допустимых значений; | 1 | |
| применяет свойства логарифма; | 1 | |||
| записывает равносильное уравнение; | 1 | |||
| находит корень уравнения; | 1 | |||
| Решает показательное неравенство | 3 | Приводит неравенство к одному основанию; | 1 | |
| решает неравенство; | 1 | |||
| находит наименьшее(наибольшее)целое число решения неравенства; | 1 | |||
| Решает логарифмическое неравенство | 4 | Применяет свойства логарифмической функции; | 1 | |
| Применяет свойство логарифма произведения(частного); | 1 | |||
| приводит неравенство к одному основанию логарифма; | 1 | |||
| определяет решение неравенства | 1 | |||
| Итого: | 15 | |||
-
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ -
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
ФИ УЧАЩЕГОСЯ____________________________________________
| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Решает показательное уравнение | Затрудняется в решении показательного уравнения | Допускает ошибки в решении показательного уравнения: в применении свойств степени; в арифметических вычислениях | Решает показательное уравнение, применяя метод введения новой переменной |
| Решает логарифмическое уравнение | Затрудняется в решении логарифмического уравнения | Допускает ошибки в решении логарифмического уравнения: в применении свойств логарифмов; в арифметических вычислениях | Применяет свойства логарифмов при решении логарифмического уравнения |
| Решает показательное неравенство | Затрудняется в решении показательного неравенства | Допускает ошибки в решении показательного неравенства: в применении свойств степени; в арифметических вычислениях | Решает показательное неравенство, применяя свойства показательной функции |
| Решает систему логарифмических неравенств | Затрудняется в решении логарифмического неравенств | Допускает ошибки в решении логарифмического неравенства; | Решает логарифмическое неравенство |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»
| Тема | Основные сведения о дифференциальных уравнениях. Дифференциальные уравнения первого порядка c разделяющимися переменными. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. |
| Цель обучения | 11.4.1.23 Знать определения частного и общего решений дифференциального уравнения 11.4.1.24 Решать дифференциальные уравнения с разделяющимися переменными 11.4.3.1 Применять дифференциальные уравнения при решении физических задач 11.4.1.25 Решать линейные однородные дифференциальные уравнениявторого порядка (вида ay''+by'+cy=0 ,где a,b,c - постоянные) |
| Критерий оценивания | Обучающийся Использует дифференциальное уравнение при решении физической задачи Решает дифференциальное уравнение с разделяющимися переменными Решает линейное однородное дифференциальное уравнение второго порядка (вида ay''+by'+cy=0 ,где a,b,c - постоянные) |
| Уровень мыслительных навыков | Применение Навыки высокого порядка |
| Время выполнения | 40 минут |
ЗАДАНИЯ
| Оценивание заданий работы | |||
| № задания | 1 | 2 | 3 |
| Количество баллов | 5 | 6 | 7 |
| Всего баллов | 18 баллов | ||
1 ВАРИАНТ
-
Найдите общее решение дифференциального уравнения:
-
Найдите частное решение уравнения y′ + 3y′ = 0 , удовлетворяющее начальным условиям y(0) = 2 , y′(0) = 3. -
Скорость точки равна V=0,1t3м/сек. Найти путь S, пройденный точкой за промежуток времени t=10 сек от начала движения.
2 ВАРИАНТ
-
Найдите общее решение дифференциального уравнения:
-
Найдите частное решение уравнения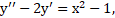
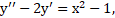удовлетворяющее начальным условиям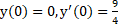 
-
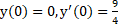
Скорость точки равна V=(t 3+0,2t) м/сек. Найти путь S , пройденный точкой за промежуток времени t=10 сек от начала движения.
3 ВАРИАНТ
-
Найдите общее решение дифференциального уравнения:
