Файл: Инструкция по регистрации на портале дистанционного образования moodle 3.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 356
Скачиваний: 1
СОДЕРЖАНИЕ
Инструкция по регистрации на портале дистанционного образования MOODLE
КРЕДИТ 1. ВЫБОРОЧНЫЙ МЕТОД В НАУЧНЫХ ИССЛЕДОВАНИЯХ
РАЗДЕЛ 1. ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Практическое занятие 1: Построение и описание гистограмм
Практическое занятие 2. Вычисление статистических характеристик случайных величин
Практическое занятие 3. Проверка гипотезы о нормальности распределения случайной величины.
Задание к теме: Проверка гипотезы о нормальности распределения случайной величины.
РАЗДЕЛ 2. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Практическое занятие 4. Критерий Стьюдента для анализа биомедицинских данных.
Практическое занятие 5. Непараметрические критерии проверки статистических гипотез.
Практическое занятие 6. Сравнение относительных величин
РАЗДЕЛ 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ
Практические занятие 7. Таблицы сопряженности
Практическое занятие 8. Линейная корреляция.
Практическое занятие 9. Прогнозирование на основе линейной регрессии
Практическое занятие 10. Метод однофакторного дисперсионного анализа.
Критические значения коэффициента асимметрии As
Критические значения коэффициента эксцесса Ех
Критические точки двустороннего t-критерия Стьюдента
Задание к теме: Выполняется на платформе MOODLE
На платформе «MOODLE» найдите дисциплину «Биостатистика» и задание по СРСП 2 согласно своему варианту. После его выполнения введите ответы. Задание должно быть выполнено в течение срока изучения РАЗДЕЛА 1.
Для расчетов использовать программу EXCELL мастер функций fx категорию «статистические» функции СРЗНАЧ, ДИСП В, СТАНД ОТКЛ В и другие.
Для вычисления квартилей использовать функцию КВАРТИЛЬ ВКЛ «1» для нижнего и «3» для верхнего квартилей.
Практическое занятие 3. Проверка гипотезы о нормальности распределения случайной величины.
Для проверки нормальности распределения случайной величины можно использовать коэффициент ассиметрии и коэффициент эксцесса.
Коэффициент ассиметрии As– показатель отклонения кривой распределения от симметричности.
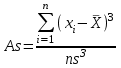
О
 трицательный коэффициент ассиметрии означает, что кривая распределения скошена влево от центра, положительный – вправо. При нормальном распределении Asблизок к нулю.
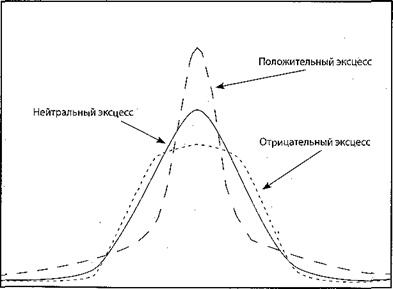
трицательный коэффициент ассиметрии означает, что кривая распределения скошена влево от центра, положительный – вправо. При нормальном распределении Asблизок к нулю.Коэффициент эксцесса Exхарактеризует степень заостренности кривой распределения (положительный коэффициент свидетельствует о об более острой вершине, отрицательный– о более пологой).
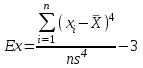
Для нормального распределения эти коэффициенты должны быть близки нулю. Но, поскольку они являются выборочными, то на практике точное равенство нулю почти не встречается. Поэтому для проверки нормальности распределения рекомендуется использовать соответствующие таблицы (Приложение), в которых указаны критические точки для этих коэффициентов при различных уровнях значимости и объемах выборки.
-
Если оба рассчитанные значение для ассиметрии и эксцесса по модулю меньше этих критических точек, гипотеза о нормальности распределения принимается. -
Если хотя бы один коэффициент больше критического значения, то распределение отличается от нормального
Пример. Проверить на нормальность распределения систолического артериального давления по выборке из 25 значений.
| 130 | 120 | 125 | 130 | 100 | 110 | 125 | 130 | 145 | 140 | 140 | 155 | 135 |
| 145 | 125 | 120 | 110 | 100 | 95 | 125 | 130 | 110 | 135 | 140 | 155 | |
Н(0): распределение систолического давления соответствует нормальному распределению
Выполним вычисления
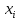 | 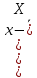 | 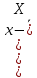 | 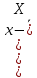 | 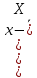 |
| 130 | 3 | 9 | 27 | 81 |
| 120 | -7 | 49 | -343 | 2401 |
| 125 | -2 | 4 | -8 | 16 |
| 130 | 3 | 9 | 27 | 81 |
| 100 | -27 | 729 | -19683 | 531441 |
| 110 | -17 | 289 | -4913 | 83521 |
| 125 | -2 | 4 | -8 | 16 |
| 130 | 3 | 9 | 27 | 81 |
| 145 | 18 | 324 | 5832 | 104976 |
| 140 | 13 | 169 | 2197 | 28561 |
| 140 | 13 | 169 | 2197 | 28561 |
| 155 | 28 | 784 | 21952 | 614656 |
| 135 | 8 | 64 | 512 | 4096 |
| 145 | 18 | 324 | 5832 | 104976 |
| 125 | -2 | 4 | -8 | 16 |
| 120 | -7 | 49 | -343 | 2401 |
| 110 | -17 | 289 | -4913 | 83521 |
| 100 | -27 | 729 | -19683 | 531441 |
| 95 | -32 | 1024 | -32768 | 1048576 |
| 125 | -2 | 4 | -8 | 16 |
| 130 | 3 | 9 | 27 | 81 |
| 110 | -17 | 289 | -4913 | 83521 |
| 135 | 8 | 64 | 512 | 4096 |
| 140 | 13 | 169 | 2197 | 28561 |
| 155 | 28 | 784 | 21952 | 614656 |
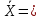 127 127 | | ∑=6350 | ∑=-24300 | ∑=3900350 |
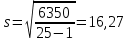
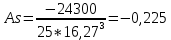
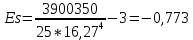
| п =25 | 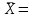 127 127 | s=16,27 | As=-0,225 | Ex=-0,773 | α=0,05 | Asрит=0,711 | Exкрит=0,869 |
Поскольку вычисленные значения коэффициентов по модулю меньше соответствующих табличных (см. Приложение), то принимается нулевая гипотеза, т.е. распределение соответствует нормальному.
Контрольные вопросы
-
Что понимается под термином «распределение» -
Классификация признаков, к каким признакам применимо понятие распределение -
Что характеризуют коэффициент ассиметрии и коэффициент эксцесса. -
Какими свойствами обладает нормальное распределение -
Как проверить нормальность распределения
Задание к теме: Проверка гипотезы о нормальности распределения случайной величины.
По данным из таблицы построить гистограмму распределения, провести эмпирическую кривую распределения, вычислить коэффициенты ассиметрии и эксцесса, проверить гипотезу о нормальности распределения.
| ВАРИАНТ | |||||||||||||||
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| | Рост, см | Рост, см | Содержание Р в слюне, ммоль\л | Содержание Р в слюне, ммоль\л | Вес, кг | Вес, кг | Объем циркулирующей плазмы, мл\кг | Объем циркулирующей плазмы, мл\кг | Пульс, уд\мин | Пульс, уд\мин | Показатель гематокрита | Показатель гематокрита | Концентрация пролактина в крови (нг/мл) | Содержание андростеронов в моче (мг/сутки) | Концентрация пролактина в крови (нг/мл) |
| | 196 | 167 | 7 | 2,2 | 65 | 58 | 45 | 34 | 66 | 76 | 0,26 | 0,48 | 25 | 0,82 | 36 |
| | 175 | 177 | 3,7 | 4,5 | 70 | 70 | 36 | 32 | 72 | 72 | 0,12 | 0,1 | 120 | 0,9 | 120 |
| | 181 | 165 | 5,5 | 4,7 | 75 | 75 | 37 | 39 | 77 | 82 | 0,2 | 0,22 | 75 | 0,98 | 88 |
| | 181 | 195 | 3,1 | 2,3 | 68 | 88 | 38 | 42 | 80 | 80 | 0,28 | 0,16 | 50 | 1,06 | 50 |
| | 184 | 181 | 3,9 | 3,8 | 92 | 92 | 41 | 46 | 58 | 90 | 0,29 | 0,41 | 185 | 1,2 | 166 |
| | 154 | 194 | 4,5 | 5,7 | 88 | 81 | 42 | 41 | 75 | 75 | 0,21 | 0,23 | 125 | 1,29 | 125 |
| | 173 | 178 | 5,7 | 2,9 | 76 | 76 | 26 | 38 | 82 | 88 | 0,45 | 0,14 | 70 | 1,48 | 82 |
| | 169 | 177 | 4 | 5,9 | 73 | 66 | 31 | 28 | 78 | 78 | 0,38 | 0,33 | 145 | 1,42 | 145 |
| | 169 | 191 | 3,7 | 3,1 | 77 | 77 | 35 | 39 | 71 | 76 | 0,29 | 0,34 | 170 | 1,4 | 144 |
| | 163 | 175 | 6 | 6,7 | 102 | 90 | 40 | 27 | 62 | 62 | 0,24 | 0,35 | 80 | 1,08 | 80 |
| | 174 | 155 | 3,8 | 4,4 | 85 | 85 | 43 | 43 | 78 | 66 | 0,27 | 0,27 | 110 | 1,11 | 57 |
| | 192 | 175 | 5,4 | 4,7 | 69 | 100 | 36 | 33 | 76 | 76 | 0,18 | 0,24 | 87 | 1,32 | 87 |
| | 176 | 165 | 6,1 | 3,6 | 70 | 70 | 37 | 44 | 82 | 80 | 0,23 | 0,3 | 115 | 1,12 | 99 |
| | 177 | 170 | 3,9 | 6,9 | 77 | 52 | 36 | 34 | 82 | 82 | 0,3 | 0,17 | 130 | 1,26 | 130 |
| | 177 | 161 | 4,4 | 5,6 | 82 | 82 | 30 | 40 | 66 | 85 | 0,32 | 0,11 | 58 | 0,88 | 69 |
| | 180 | 178 | 5,6 | 3,5 | 66 | 77 | 26 | 31 | 60 | 78 | 0,18 | 0,15 | 122 | 1,16 | 122 |
| | 177 | 178 | 3,8 | 6,4 | 75 | 75 | 44 | 26 | 75 | 75 | 0,42 | 0,3 | 78 | 1,3 | 80 |
| | 155 | 176 | 2,4 | 3 | 69 | 88 | 30 | 33 | 78 | 75 | 0,36 | 0,28 | 110 | 1,2 | 110 |
| | 174 | 178 | 2,5 | 6,6 | 83 | 83 | 40 | 36 | 72 | 72 | 0,26 | 0,4 | 66 | 0,84 | 70 |
| | 167 | 185 | 3,6 | 4,7 | 74 | 70 | 31 | 37 | 68 | 80 | 0,29 | 0,23 | 92 | 0,96 | 92 |
| | 174 | 155 | 3,8 | 4,4 | 85 | 85 | 43 | 43 | 78 | 66 | 0,27 | 0,27 | 110 | 1,11 | 57 |
| | 192 | 175 | 5,4 | 4,7 | 69 | 100 | 36 | 33 | 76 | 76 | 0,18 | 0,24 | 87 | 1,32 | 87 |
| | 176 | 165 | 6,1 | 3,6 | 70 | 70 | 37 | 44 | 82 | 80 | 0,23 | 0,3 | 115 | 1,12 | 99 |
| | 177 | 170 | 3,9 | 6,9 | 77 | 52 | 36 | 34 | 82 | 82 | 0,3 | 0,17 | 130 | 1,26 | 130 |
| | 177 | 161 | 4,4 | 5,6 | 82 | 82 | 30 | 40 | 66 | 85 | 0,32 | 0,11 | 58 | 0,88 | 69 |
| | 180 | 178 | 5,6 | 3,5 | 66 | 77 | 26 | 31 | 60 | 78 | 0,18 | 0,15 | 122 | 1,16 | 122 |
| | 177 | 178 | 3,8 | 6,4 | 75 | 75 | 44 | 26 | 75 | 75 | 0,42 | 0,3 | 78 | 1,3 | 80 |
| | 155 | 176 | 2,4 | 3 | 69 | 88 | 30 | 33 | 78 | 75 | 0,36 | 0,28 | 110 | 1,2 | 110 |
| | 174 | 178 | 2,5 | 6,6 | 83 | 83 | 40 | 36 | 72 | 72 | 0,26 | 0,4 | 66 | 0,84 | 70 |
| | 167 | 185 | 3,6 | 4,7 | 74 | 70 | 31 | 37 | 68 | 80 | 0,29 | 0,23 | 92 | 0,96 | 92 |