Файл: Руководство по выполнению базовых экспериментов эцпет. 001 Рбэ (902) 2006.doc

непосредственно перед коммутацией, т. е. скачком не меняется.

В данной работе коммутация (включение и выключение) осуществляется транзистором, на базу которого подаются отпирающие импульсы тока от источника синусоидального напряжения с частотой 50 Гц. В результате оба переходных процесса периодически повторяются и их можно наблюдать на осциллографе.

10.1.2. Экспериментальная часть

Задание
Рассчитать докоммутационные (t = - 0), начальные (t = + 0) и установившиеся (t

) значения токов и напряжения на конденсаторе в цепи (рис. 10.1.1) в двух случаях: 1. - ключ замыкается; 2. - ключ размыкается.

Рис. 10.1.1
В каждом из этих случаев определить постоянную времени цепи, снять осциллограммы рассчитанных величин и убедиться, что все токи и напряжение на конденсаторе изменяются с одной постоянной времени, а напряжение на конденсаторе не имеет скачков.
Порядок выполнения работы

При включении ключа в цепи (рис. 10.1.1) рассчитайте токи и напряжение на конденсаторе до коммутации (t = - 0, ключ разомкнут), в первый момент после коммутации (t = + 0, ключ замкнут) и в новом установившемся режиме (t ). Результаты расчёта занесите в табл. 10.1.1.
Повторите расчёт при размыкании ключа. Результаты занесите также в табл. 10.1.2.
Составьте характеристическое уравнение, определите корень р и постоянную времени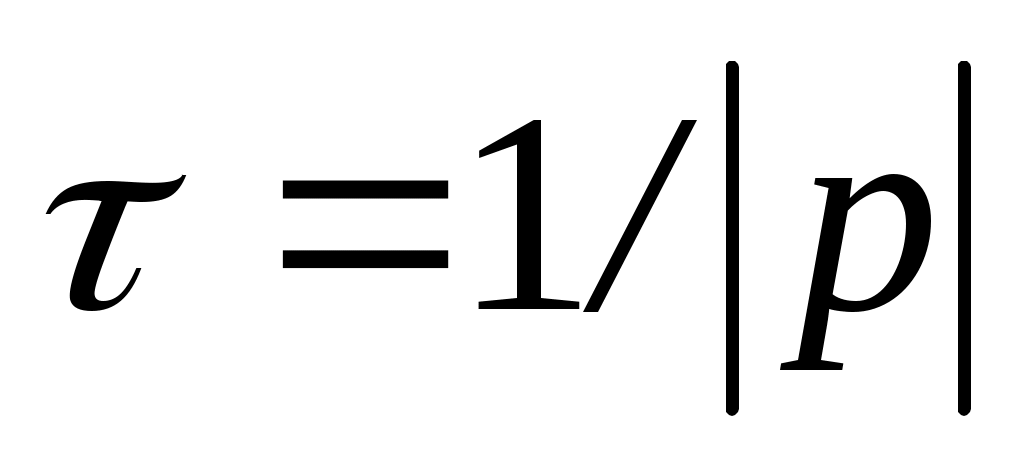 для первого и для второго случаев, занесите результаты в табл. 10.1.1 и 10.1.2.
Соберите цепь согласно схеме (рис.10.1.2), включив в неё вместо изображенных измерительных приборов соответствующие гнёзда коннектора. Обратите внимание на полярность электролитического конденсатора.
Включите осциллограф, установите развёртку 2 мС/дел и перерисуйте изображение четырёх измеряемых величин на график (рис.10.1.3). Не забудьте указать масштаб для каждой кривой.
Определите по графику или непосредственно по осциллографу докоммутационные (t = - 0) начальные (t = + 0) и установившиеся (t ) значения токов и напряжения на конденсаторе в цепи в двух случаях: 1. - ключ замыкается; 2. - ключ размыкается. Занесите их также в табл. 10.1.1 и10.1.2 и сравните с расчётными.

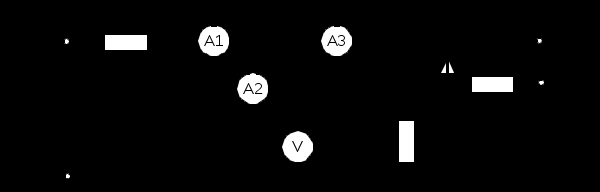
Рис. 10.1.2

Определите по графикам постоянные времени при замыкании и размыкании ключа. Сравните их с расчётными значениями и занесите в табл. 10.1.1 и 10.1.2.
Проанализируйте результаты и сделайте выводы.

- ключ замыкается

Таблица 10.1.1

t	u_C, В	i₁, ьА	i₂, мА	i₃, мА	, мС
- 0, расчёт - 0, эксперимент					Расчёт:  = мС Эксперимент:  = мС
+ 0, расчёт + 0, эксперимент
, расчёт , эксперимент

- ключ размыкается

Таблица 10.1.1

t	u_C, В	i₁, ьА	i₂, мА	i₃, мА	, мС
- 0, расчёт - 0, эксперимент					Расчёт:  = мС Эксперимент:  = мС
+ 0, расчёт + 0, эксперимент
, расчёт , эксперимент

Рис.10.1.2

10.2. Процессы включения и отключения цепи с катушкой индуктивности

10.2.1 Общие сведения

Цепь с одной катушкой индуктивности, так же как и цепь с одним конденсатором описывается дифференциальным уравнением первого порядка. Поэтому все токи и напряжения в переходном режиме изменяются по экспоненциальному закону с одной и той же постоянной времени (

) от начального значения до установившегося. Причём, начальное значение тока в индуктивности равно току в ней непосредственно перед коммутацией, так как ток в катушке не может изменяться скачком по закону коммутации. Напряжение на катушке может изменяться скачком и при отключении может достигать весьма больших значений.

В данной работе коммутация (включение и выключение цепи) осуществляется транзистором, на базу которого подаются однополярные прямоугольные отпирающие импульсы тока от генератора напряжений специальной формы с частотой 200 Гц. Поэтому

оба переходных процесса периодически повторяются и их можно наблюдать на обычном или виртуальном осциллографе.

10.2.2. Экспериментальная часть

Задание
Вывести на дисплей виртуального осциллографа кривые тока и напряжения на катушке индуктивности при подключении и отключении источника постоянного напряжения. В каждом из этих случаев определить экспериментально и рассчитать докоммутационные (t = - 0), начальные (t = + 0) и установившиеся (t

) значения тока и напряжения на катушке, определить по осциллограмме постоянную времени цепи

.

Экспериментальная часть

Соберите цепь согласно схеме (рис.10.2.2), включив в неё вместо изображенных измерительных приборов соответствующие гнёзда коннектора.

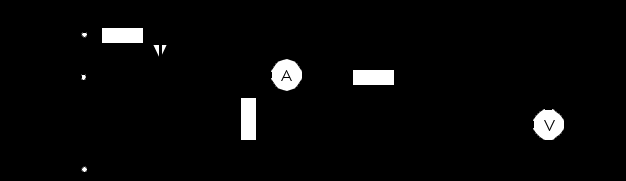
Рис. 10.2.1

Включите осциллограф, установите развёртку 0,5 мС/дел и перерисуйте изображение тока и напряжения на катушке на график (рис.10.2.2). Не забудьте указать масштаб для каждой кривой.
Определите по графику или непосредственно по осциллографу докоммутационные (t = - 0) начальные (t = + 0) и установившиеся (t ) значения токов и напряжений на катушке в двух случаях: 1. - ключ замыкается; 2. - ключ размыкается. Занесите их в табл. 10.2.1.
Рассчитайте токи и напряжения на катушке для этих же моментов времени, занесите результаты также в табл. 10.2.1. Сравните результаты расчёта и эксперимента.
Определите по осциллограммам постоянные времени при включенном и при отключенном источнике питания.

Таблица 10.1.1

t	Включение,  = мС		Выключение,  = мС
t	u_L, В	i_L, мА	u_L, В	i_L, мА
- 0, расчёт - 0, эксперимент
+ 0, расчёт + 0, эксперимент
, расчёт , эксперимент

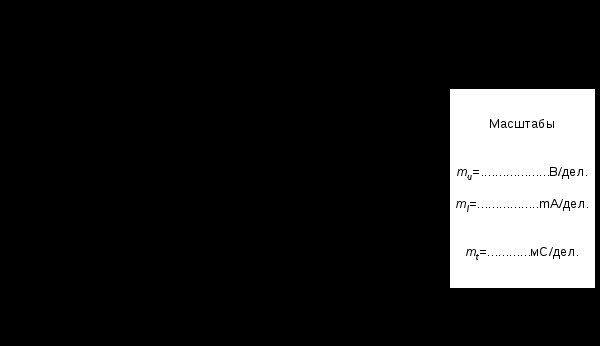
Рис.10.2.2

10.3. Затухающие синусоидальные колебания в R-L-C контуре

10.3.1. Общие сведения

В замкнутом контуре (рис. 10.3.1) после отключении его от источника постоянного или переменного напряжения могут возникнуть затухающие синусоидальные колебания, обусловленные начальным запасом энергии в электрическом поле конденсатора и в магнитном поле катушки индуктивности.

В общем случае состояние цепи определяется из дифференциального уравнения, составленного по второму закону Кирхгофа:

Поскольку

то

или

Рис. 10.3.1.
Вид решения этого дифференциального уравнения зависит от характера корней характеристического уравнения:

Корни этого уравнения:

Когда

, корни вещественные отрицательные и процесс изменения тока и напряжений имеет апериодический затухающий характер (рис.10.3.2а). Если же R<R_кр, то возникает колебательный процесс (рис. 10.3.2б). Тогда решение дифференциального уравнения имеет вид:

sint,

где

Рис. 10.3.2.
При уменьшении сопротивления от некоторого значения большего, чем Rкр сначала увеличивается скорость затухающего апериодического процесса, затем, при R=Rкр качественно изменяется характер процесса – он становится колебательным - и при дальнейшем уменьшении сопротивления увеличивается частота колебаний и уменьшается затухание. При R, стремящемся к нулю, частота стремится к резонансной частоте

, а затухание – к нулю.

В данной работе заряд конденсатора до напряжения u₀ осуществляется однополярными прямоугольными импульсами напряжения и исследуется процесс его разряда на сопротивление и индуктивность во время пауз между импульсами. Повторяющийся процесс заряда и разряда конденсатора можно наблюдать на электронном или виртуальном осциллографе.

10.3.2. Экспериментальная часть

Задание

Исследовать влияние активного сопротивления на характер процесса разряда конденсатора на сопротивление и индуктивность. Сравнить экспериментальные частоту и затухание колебаний с расчётными значениями.