Файл: Руководство по выполнению базовых экспериментов эцпет. 001 Рбэ (902) 2006.doc

: ……….

---

9. Расчёт и экспериментальное исследование цепи при несинусоидальном приложенном напряжении

(для компьютерного варианта стенда)

9.1. Общие сведения

Несинусоидальное периодическое напряжение, приложенное к электрической цепи, можно разложить в ряд Фурье:



где



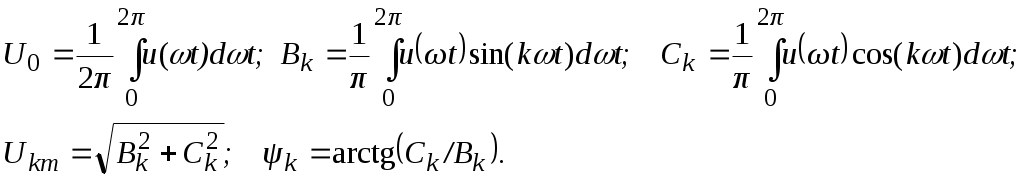
Расчёт цепи проводят с использованием принципа наложения в следующей последовательности:

• 
  рассчитывают цепь при постоянном приложенном напряжении U₀;
  
• 
  рассчитывают цепь (обычно комплексным методом) при синусоидальном приложенном напряжении с амплитудой U_1mчастоты и частотой (k=1)
  
• 
  повторяют расчёт при k = 2, 3, 4, …, учитывая, что индуктивные сопротивления увеличиваются с ростом частоты (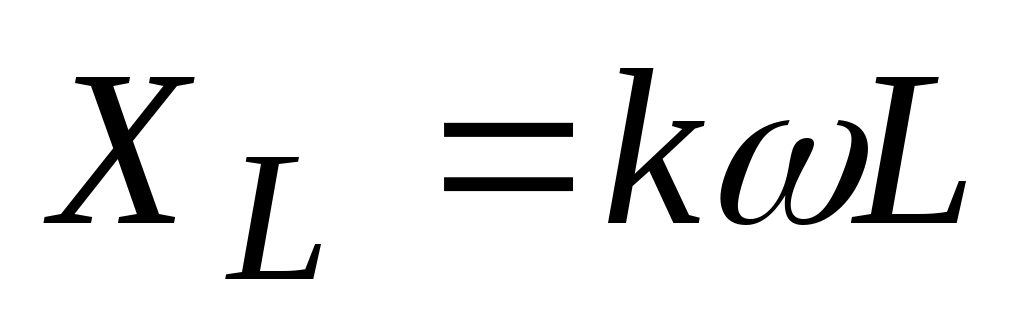 ), а ёмкостные уменьшаются ( );
  
• 
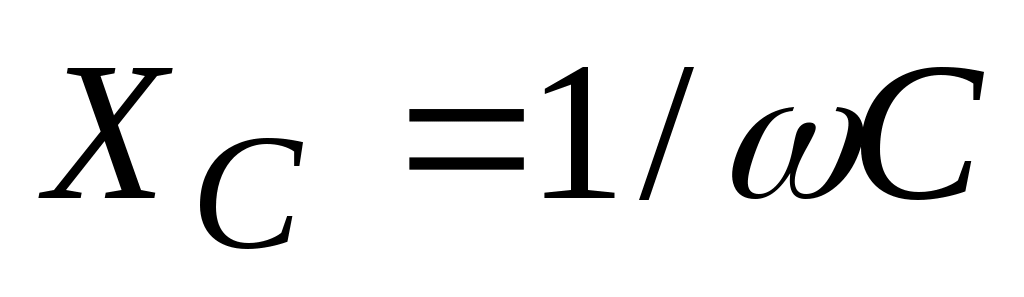  переходят к мгновенным значениям и суммируют постоянную и синусоидальные составляющие тока (напряжения) в каждой ветви;
  
• 
  определяют действующие значения токов и напряжений, а также мощности по формулам:
  
• 
  
  

где U_k, I_k – действующие значения синусоидальных составляющих.

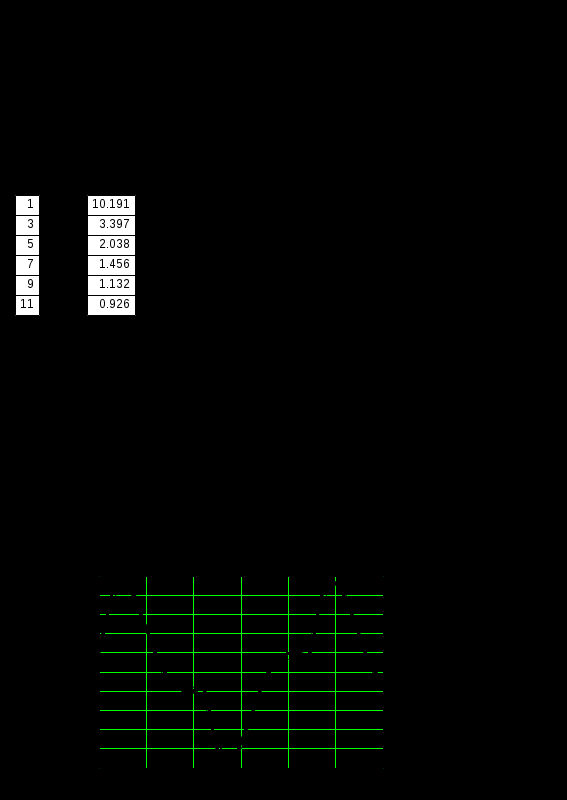
Чем больше гармоник взято для расчёта, тем выше точность полученных результатов. На рис. 9.1 приведен в качестве примера экспериментальный график тока в

цепи с последовательным соединением R, L, и C при двуполярном прямоугольном приложенном напряжении. На этот график наложены в том же масштабе два расчётных графика: один сделан с учётом только первой и третьей гармоник, а в другом учтены 5 гармоник - с первой по одиннадцатую.

В приложении приведена MathCAD-программа расчёта этих графиков с комментариями.

9.2. Экспериментальная часть

Задание

Рассчитать мгновенное и действующее значение тока и напряжения на конденсаторе, а также потребляемую цепью активную мощность при

---

прямоугольном периодическом приложенном напряжении, построить график изменения тока на входе цепи, проверить результаты расчёта путём осциллографирования и непосредственных измерений.


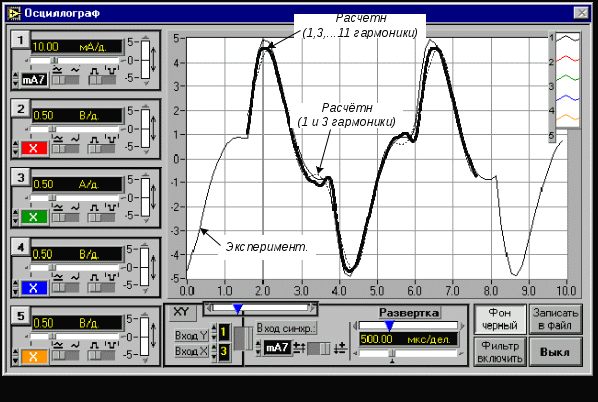
Рис. 9.1
Порядок выполнения работы

• 
  Выбрать один из приведенных ниже вариантов параметров цепи (рис. 9.2) и выполнить расчёт согласно заданию, учитывая основную гармонику и одну – две высших. По результатам расчёта мгновенных значений на рис.9.3 построить графики, а действующие значения и мощность занести в табл. 9.1.
  

Варианты параметров элементов цепи и приложенного напряжения:

L = 10 мГн (R_K=17 Ом), L = 40 мГн (R_K=70 Ом), L = 100 мГн, (R_K=170 Ом);

С = 0,22, 0,47 или 1 мкФ;

R = 47, 100, 150, или 220 Ом;

Um=8…10 B, f=0,5…1 кГц.

• 
  Собрать цепь (рис.9.2) с принятыми в расчёте параметрами элементов, включить виртуальные приборы для измерения действующих значений тока и напряжения на конденсаторе и осциллограф.
  
• 
  Установить на источнике принятые значение частоты и амплитуду прямоугольных импульсов и перенести осциллограмм на рис. 9.4. Записать в табл. 9.1 действующие значения тока и напряжения на конденсаторе.
  

Рис.9.2

• 
  Переключить вольтметр на вход цепи, включить виртуальный измеритель активной мощности и занести его показание также в табл. 9.1.
  
• 
  Сравнить результаты расчёта и эксперимента и сделать выводы.
  

Таблица 9.1

	I, мА	U, В	Р. мВт
Расчётные значения
Экспериментальные значения

Рис.9.3

---

Рис. 9.4

---

9.3. Приложение

10. Переходные процессы в линейных электрических цепях

10.1. Переходный процесс в цепи с конденсатором и резисторами

10.1.1 Общие сведения

Цепь с одним конденсатором и сопротивлениями описывается дифференциальным уравнением первого порядка, поэтому свободная составляющая тока или напряжения в любой ветви имеет одно слагаемое вида , где р – корень характеристического уравнения, а А – постоянная интегрирования.

Характеристическое уравнение может быть составлено в виде:

,

где Z(p) и Y(p) - - входные операторные сопротивление и проводимость. Они могут быть получены заменой в выражениях комплексного сопротивления или проводимости цепи аргумента j на оператор р.

Постоянные интегрирования А для каждого тока или напряжения определяется из начальных условий. Для определения постоянной А необходимо знать значение искомой функции в первый момент времени после коммутации (при t = +0).

Начальное значение напряжения на конденсаторе определяется из первого закона коммутации: u_C(+0) = u_C(-0).). В свою очередьu_C(-0 определяется из расчёта цепи до коммутации. Начальные значения других величин (токов и напряжений, которые могут изменяться скачком) рассчитываются по закону Ома и законам Кирхгофа в момент времени t= +0.

Таким образом, все токи и напряжения в переходном режиме изменяются по экспоненциальному закону с одной и той же постоянной времени ( ) от начального значения до установившегося. Причём, начальное значение напряжения на конденсаторе равно напряжению на нём

---