ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.04.2024
Просмотров: 209
Скачиваний: 0
СОДЕРЖАНИЕ
Федеральное государственное бюджетное
§2. Исследование поведения решений однородного уравнения на бесконечности
§3. Ограниченность решений однородного уравнения
§4.Условия существования ограниченного решения у неоднородного уравнения
§5. Общие сведения о дифференциальных уравнениях
Реализация метода Рунге-Кутта с помощью системы Maxima
Реализация конечно-разностного метода
§ 11. Метод сеток для решения дифференциальных уравнений в частных производных
Выполним реализацию конечно-разностного метода в системе компьютерной математики Maxima
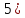 r=4,
r=4,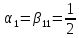 ,
,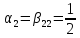 ,
,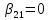 ,
,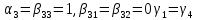 =
=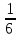 ,
,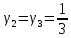 ,
l=5;
,
l=5;
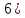 r=4,
r=4,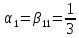 ,
,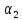 =
=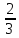 ,
,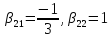 ,
,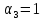 ,
,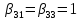 ,
,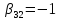 ,
,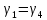 =
=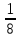 ,
,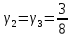 ,
l=5;
,
l=5;
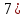 r=6,
r=6,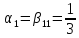 ,
,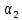 =
=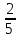 ,
,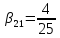 ,
,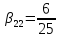 ,
,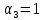 ,
,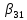 =
=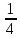 ,
,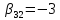 ,
,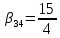 ,
,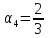 ,
,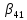 =
=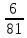 ,
,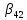 =
=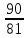 ,
,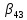 =
=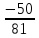 ,
,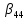 =
=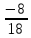 ,
,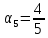 ,
,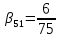 ,
,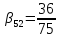 ,
,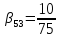 ,
,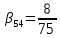 ,
,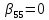 ,
,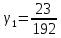 ,
,
,
,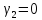 ,
,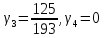 ,
,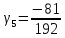 ,
,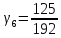
Наиболее
употребительной является система чисел
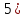 .Соответствующий
прием будем называетсяосновным
приемом Рунге-Кутта.
Приведем порядок вычислений в этом
случае.
.Соответствующий
прием будем называетсяосновным
приемом Рунге-Кутта.
Приведем порядок вычислений в этом
случае.
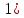 Вычисляется
Вычисляется
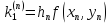 .
.
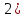 Вычисляется
Вычисляется
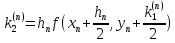 .
.
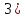 Вычисляется
Вычисляется
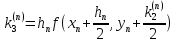 .
.
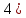 Вычисляется
Вычисляется
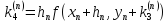 .
.
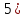 Вычисляется
Вычисляется
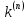 =
=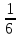 (
(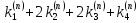 .
.
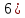 Вычисляется
Вычисляется
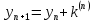 .
.
Отметим
также случай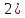 ,который
называют иногда усовершенствованным
методом Эйлера; здесь вычисления ведутся
так:
,который
называют иногда усовершенствованным
методом Эйлера; здесь вычисления ведутся
так:
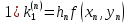 ;
;
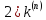 =
=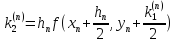 .
.
3)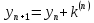
В заключении укажем на схему вычислений по методу Эйлера и Рунге-Кутта при решении задачи Коши для системы дифференциальных уравнений первого порядка. Для простоты записи ограничимся случаем системы двух уравнений.
Пусть
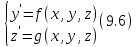
Система,
для которой требуется найти решение
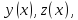 удовлетворяющую условию
удовлетворяющую условию
y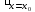 =
=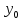 ,z
,z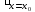 =
=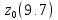
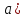 Метод
Эйлера. Вычисления проводятся по
формулам:
Метод
Эйлера. Вычисления проводятся по
формулам:
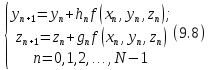
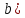 Основной
прием Рунге-Кутта. Вычисления проводятся
по формулам:
Основной
прием Рунге-Кутта. Вычисления проводятся
по формулам:
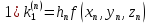 ,
,
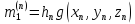 ;
;
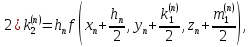
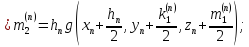
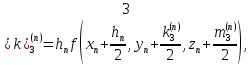
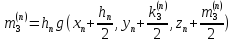 ;
;
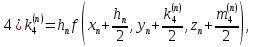
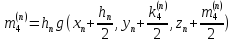 ;
;
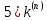 =
=
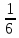 (
(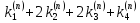 ,
,
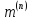 =
=
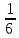 (
(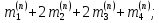
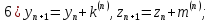
Пример
9.1. Применяя
метод Рунге-Кутта найти решение задачи
Коши
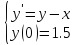 в
трех последовательных точках
в
трех последовательных точках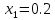 ,
,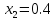 ,
,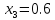 .
.
Решение.
Возьмем
шаг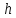 =0.2.
Используя расчетные формулы Рунге-Кутта
(9.3), найдем приближенное решение задачи
Коши:
=0.2.
Используя расчетные формулы Рунге-Кутта
(9.3), найдем приближенное решение задачи
Коши:
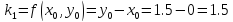
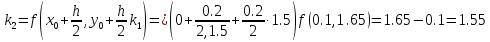
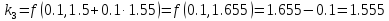
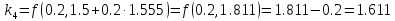
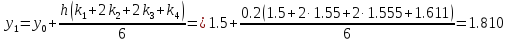
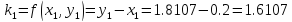
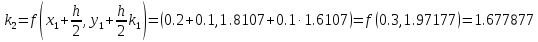
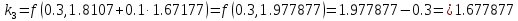
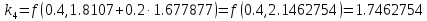
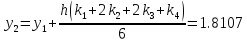 +
+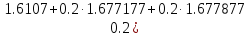 +
+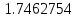 )/6=2.14590898
)/6=2.14590898
Аналогично
получаем
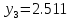 053228172
053228172
Таким образом, получили численное решение задачи Коши:
|
|
0 |
0.2 |
0.4 |
0.6 |
|
|
1.5 |
1.8107 |
2.14590898 |
2.511053228172 |
Графиком
приближенного решения является ломанная,
последовательно соединяющая точки (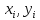 ).
).
Реализация метода Рунге-Кутта с помощью системы Maxima
В системе Maxima для нахождения численного решения задачи Коши
методом
Рунге - Кутта (четвертого порядка
точности) есть встроенная функция
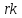 .
Для того, чтобы она стала активной,
требуется подключить пакет dynamics с
помощью команды:
.
Для того, чтобы она стала активной,
требуется подключить пакет dynamics с
помощью команды:
![]()
Теперь задаем команду для нахождения решения:
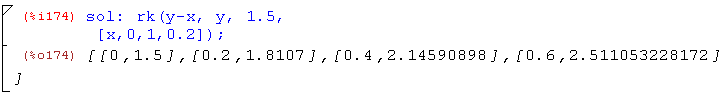
Выполним построение найденного решения задачи средствами
пакета draw:
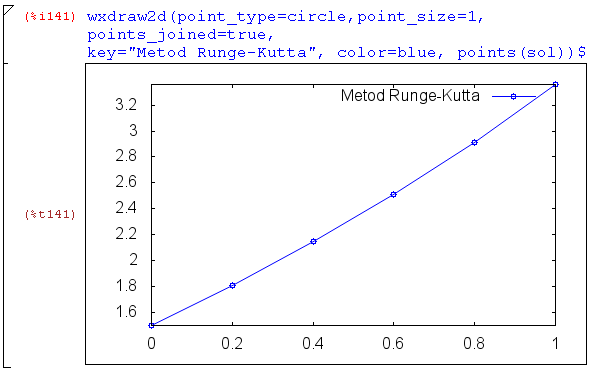
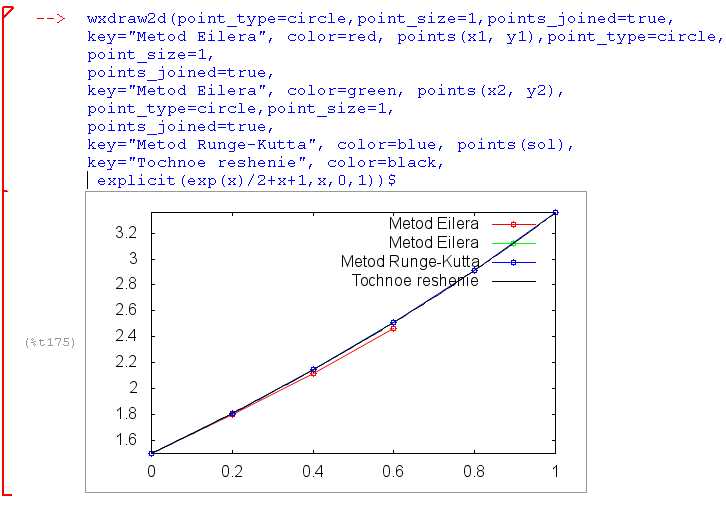
Точное решение поставленной задачи ищется в виде:
§10. Решение краевых задач для линейных дифференциальных уравнений второго порядка методом конечных разностей
Линейное дифференциальное уравнение второго порядка имеет вид
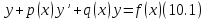
где
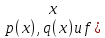 )
– некоторые, непрерывные на [a,b]
функции. Краевая задача для линейного
дифференциального уравнения состоит
в нахождении его решения
)
– некоторые, непрерывные на [a,b]
функции. Краевая задача для линейного
дифференциального уравнения состоит
в нахождении его решения
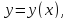 удовлетворяющего
двухточечным линейным краевым условиям
удовлетворяющего
двухточечным линейным краевым условиям
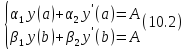
где
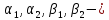 постоянные и
постоянные и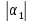 +
+ ,
,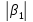 +
+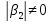
При
решении этой задачи методом конечных
разностей отрезок разбивают на равные
части с шагом
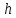 ,
где
,
где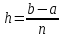 .
Точки разбиения имеют абсциссы
.
Точки разбиения имеют абсциссы
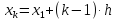 ,
,
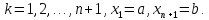
Значения
в точках деления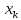 искомой функции и ее производных
искомой функции и ее производных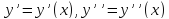 обозначим
соответственно через
обозначим
соответственно через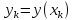 ,
,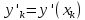 ,
,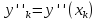 .Заменяя
производные правыми односторонними
конечно-разностными отношениями для
внутренних точек отрезка
.Заменяя
производные правыми односторонними
конечно-разностными отношениями для
внутренних точек отрезка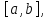 приближенно
будем иметь
приближенно
будем иметь