ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 241
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
§1. Вывод уравнения колебаний струны, постановка задач
§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера**
§3. Корректность задач математической физики. Пример некорректной задачи
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений)
§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений)
§6. Свободные колебания ограниченной струны. Метод Фурье* (метод разделения переменных)
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных)
,
где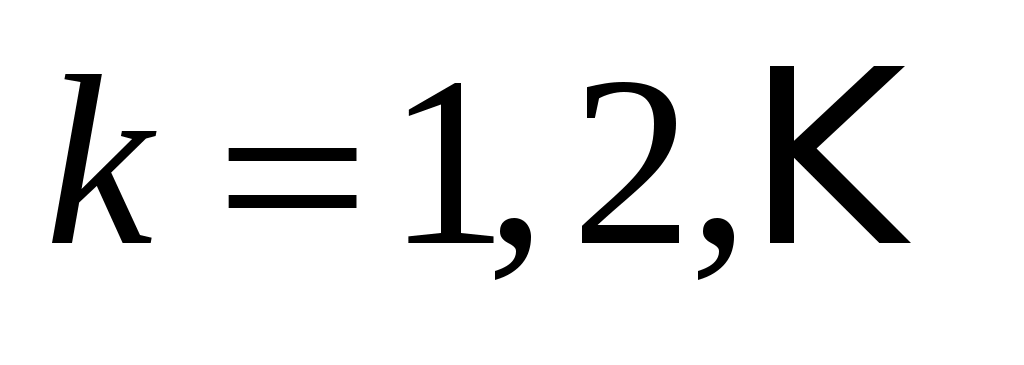 (отрицательные k не рассматриваем, так как изменение знака k равносильно изменению знака произвольной постоянной
(отрицательные k не рассматриваем, так как изменение знака k равносильно изменению знака произвольной постоянной 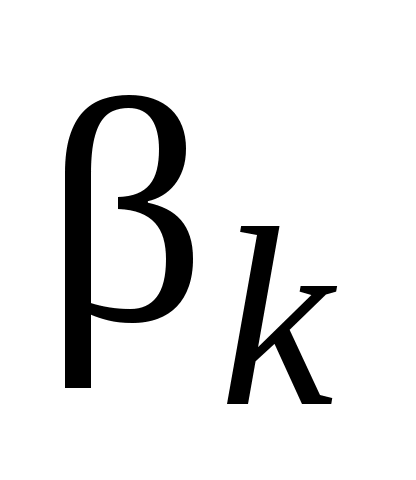 ).
).
Найденные значения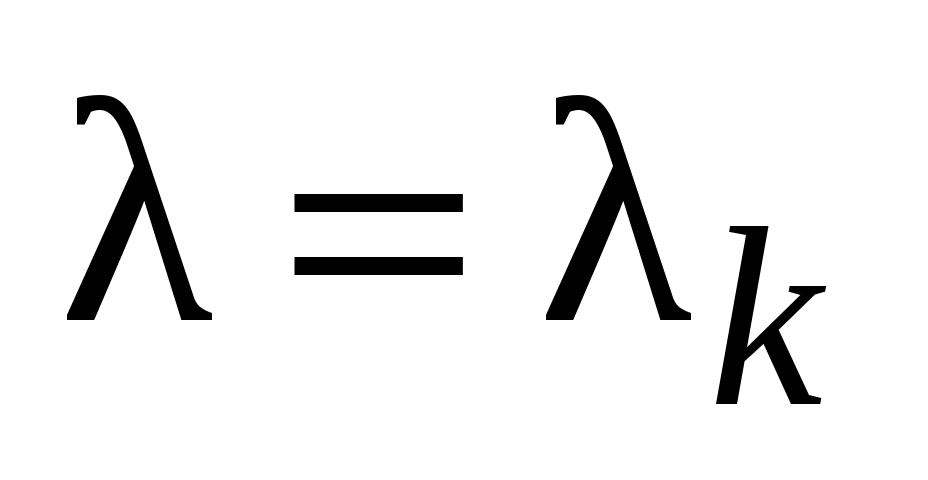 подставим в уравнение для
подставим в уравнение для 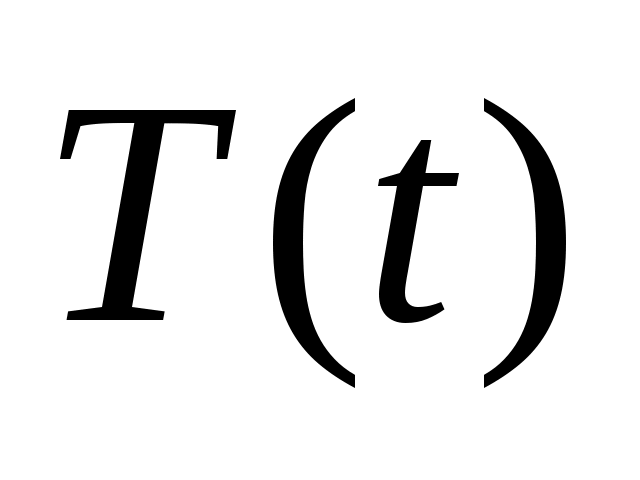 , общее решение которого имеет вид
, общее решение которого имеет вид
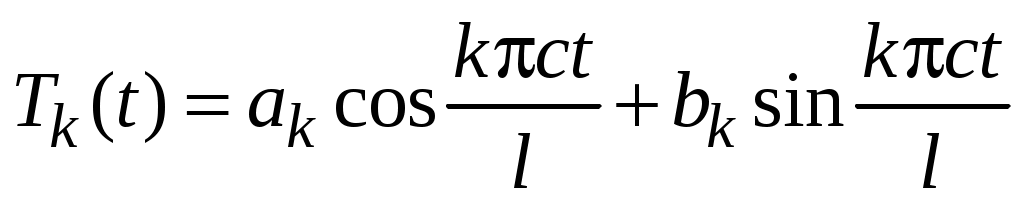 .
.
В результате получен счетный набор частных (линейно независимых) решений уравнения (3), удовлетворяющих ГУ (35):
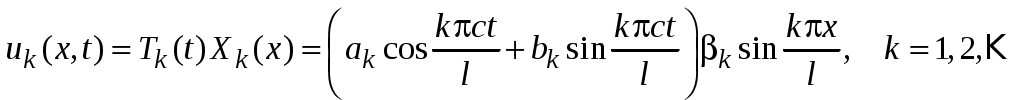 .
.
Переобозначим произвольные постоянные: заменим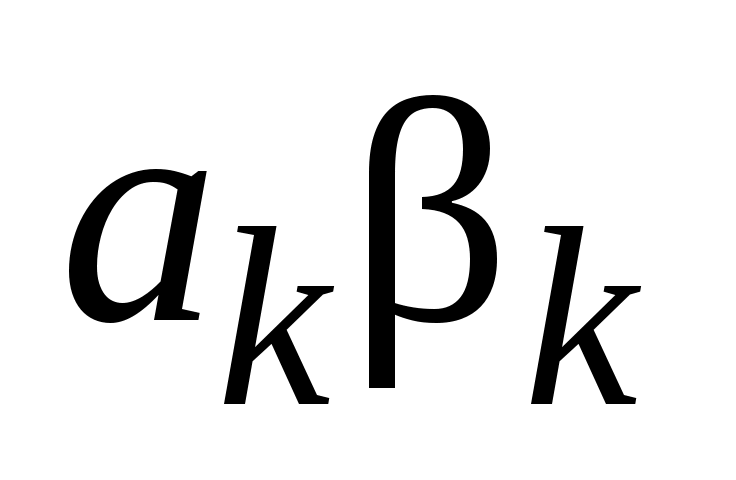 на
на 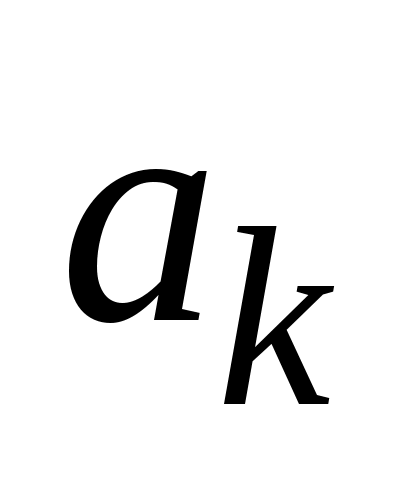 ,
, 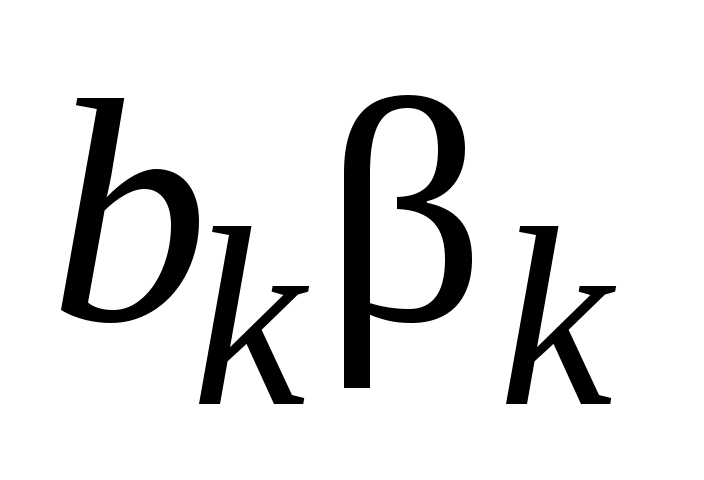 на
на 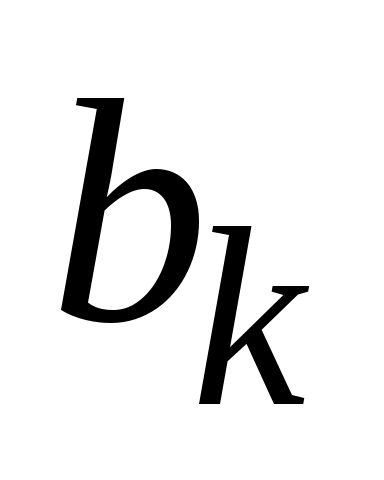 .
.
Благодаря линейности и однородности уравнения (3) и ГУ (35), любая линейная комбинация функций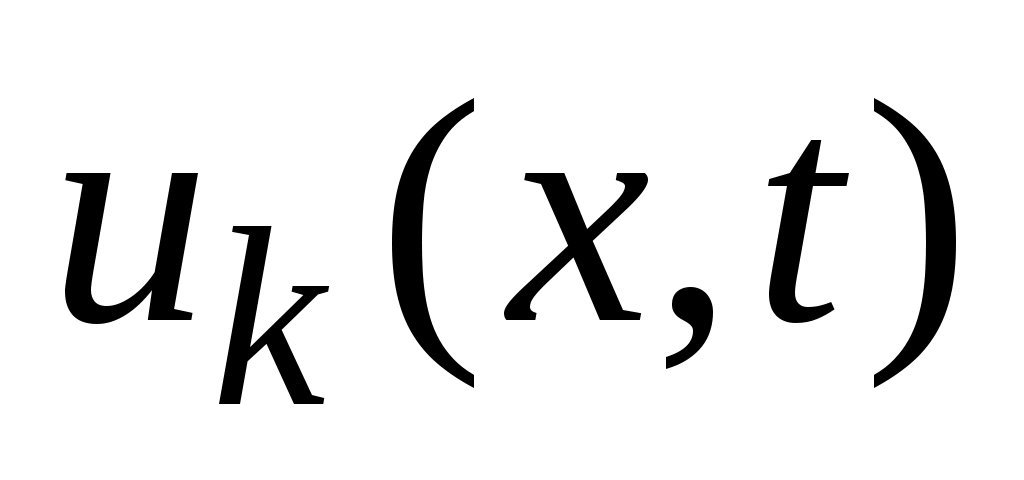 также будет удовлетворять уравнению и этим условиям. Составим ряд
также будет удовлетворять уравнению и этим условиям. Составим ряд
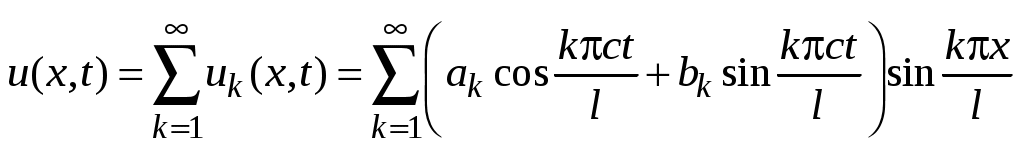 . (42)
. (42)
Сумма ряда удовлетворяет уравнению (3) и ГУ (35). Подберем постоянные
удовлетворяет уравнению (3) и ГУ (35). Подберем постоянные 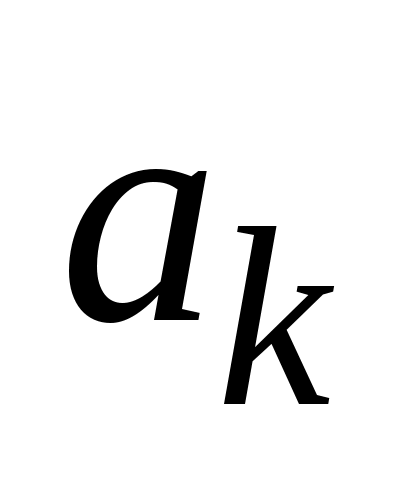 и
и 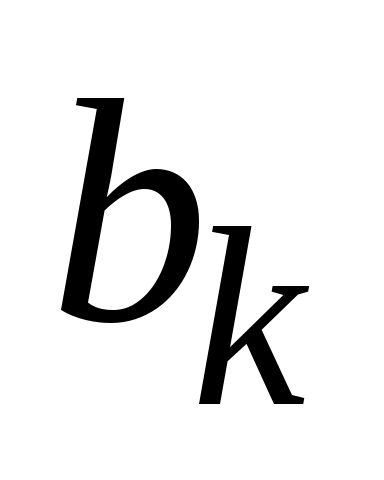 так, чтобы она удовлетворяла также НУ (34). Прямая подстановка дает
так, чтобы она удовлетворяла также НУ (34). Прямая подстановка дает
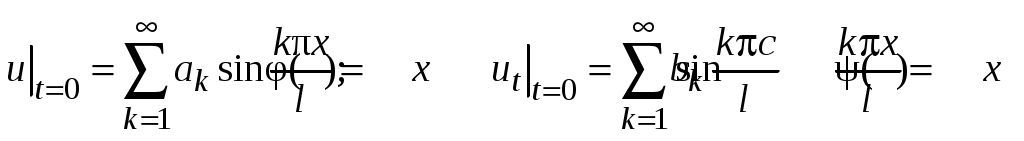 .
.
Написанные ряды представляют собой разложения заданных функций и
и  в ряды Фурье по синусам на промежутке
в ряды Фурье по синусам на промежутке  . Коэффициенты этих разложений определяются по известным формулам:
. Коэффициенты этих разложений определяются по известным формулам:
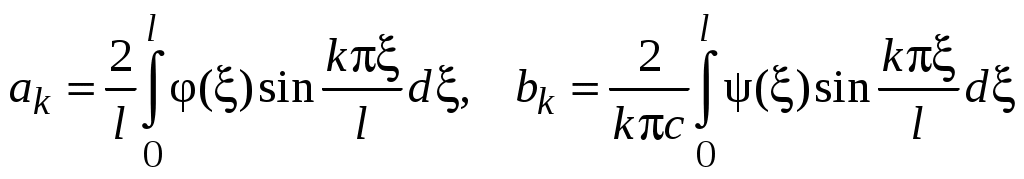 . (43)
. (43)
Ряд (42) с коэффициентами (43) формально удовлетворяет всем условиям поставленной задачи (3), (34), (35).
Нетрудно проверить, что решение в виде ряда совпадает с тем, которое было получено в § 5 методом отражений. При применении формулы Даламбера к ограниченной струне с закрепленными концами мы продолжали функции и
и  , задающие НУ, с
, задающие НУ, с  на
на 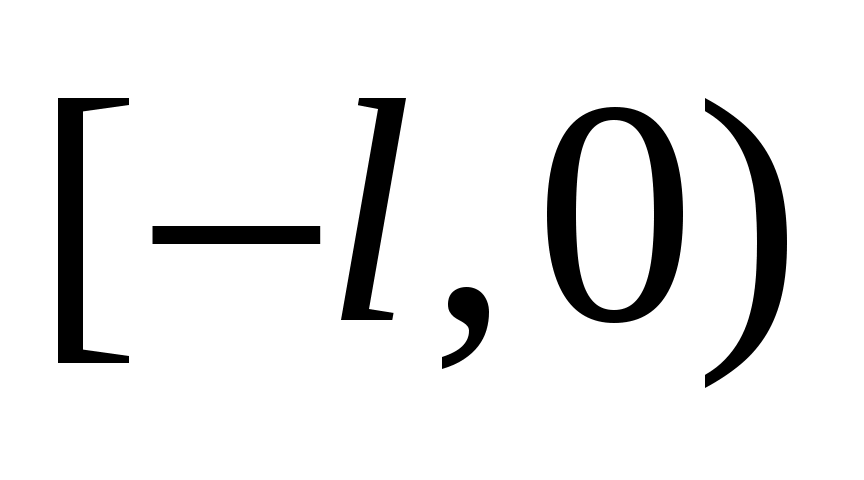 по закону нечетности и потом с периодом 2l − на всю вещественную ось. Такой способ продолжения равносилен разложению этих функций в ряды Фурье по синусам.
по закону нечетности и потом с периодом 2l − на всю вещественную ось. Такой способ продолжения равносилен разложению этих функций в ряды Фурье по синусам.
Упражнение 11. Разложить продолженные функции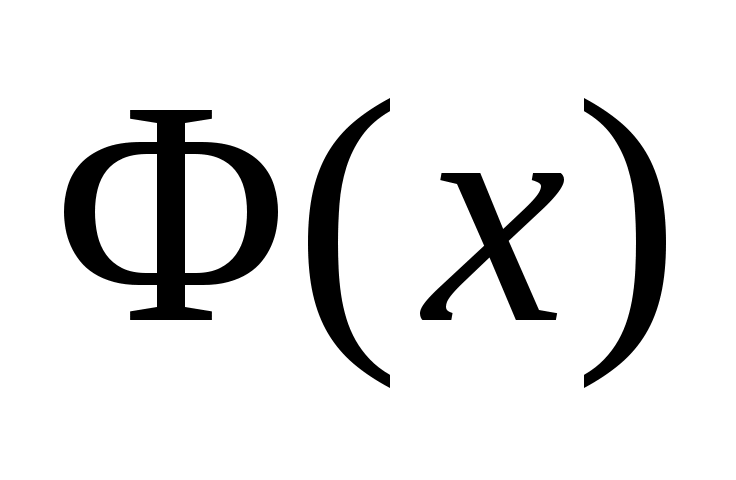 ,
, 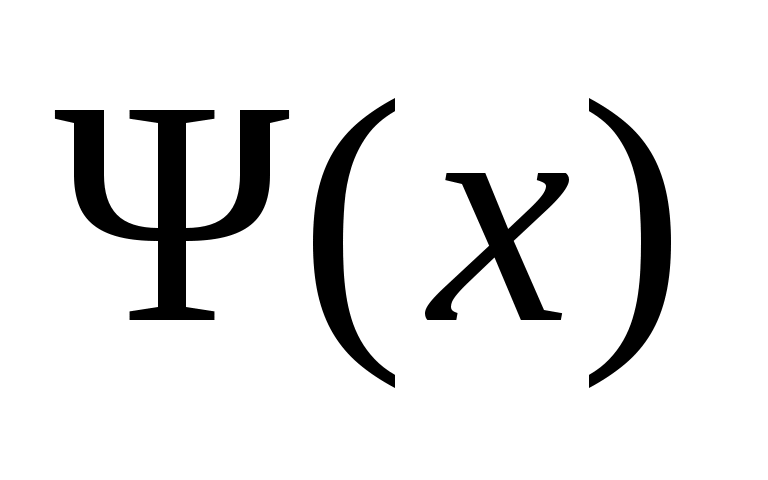 в ряды Фурье по синусам, подставить их в формулу Даламбера (36) и проверить, что полученное представление эквивалентно (42).
в ряды Фурье по синусам, подставить их в формулу Даламбера (36) и проверить, что полученное представление эквивалентно (42).
Упражнение 12. Решить методом Фурье задачу о свободных колебаниях ограниченной струны с двумя свободными концами и одним закрепленным, а другим свободным концом.
Об оправдании метода Фурье. Формально ряд (42) удовлетворяет уравнению и всем дополнительным условиям поставленной НКЗ. Возникает важный вопрос: при каких условиях на функции и
и  сам этот ряд сходится и сходятся ряды его первых и вторых производных? Ссылаясь на теорию рядов Фурье, можно сформулировать следующие достаточные условия: если функция
сам этот ряд сходится и сходятся ряды его первых и вторых производных? Ссылаясь на теорию рядов Фурье, можно сформулировать следующие достаточные условия: если функция  дважды непрерывно дифференцируема и имеет кусочно-непрерывную третью производную, функция
дважды непрерывно дифференцируема и имеет кусочно-непрерывную третью производную, функция  один раз непрерывно-дифференцируема и имеет кусочно-непрерывную вторую производную и, кроме того,
один раз непрерывно-дифференцируема и имеет кусочно-непрерывную вторую производную и, кроме того, 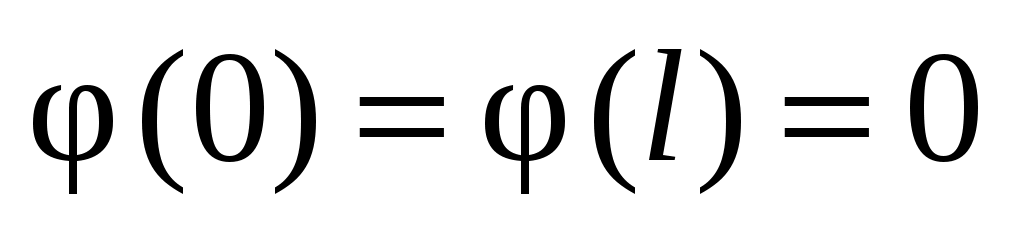
,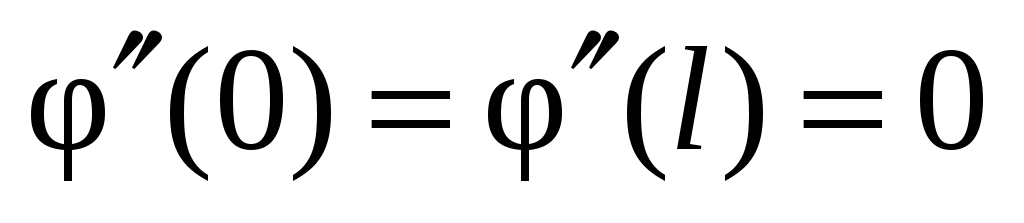 ,
, 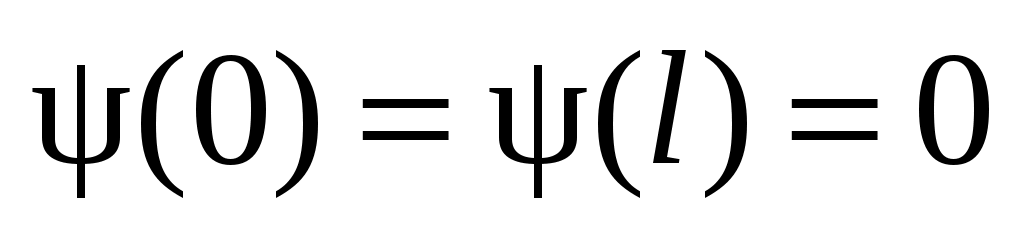 , ряд (42) сходится абсолютно и равномерно и его можно дважды почленно дифференцировать по x и t. Иными словами, ряд (42) дает классическое решение НКЗ (3), (34), (35) и его можно исследовать “в лоб”.
, ряд (42) сходится абсолютно и равномерно и его можно дважды почленно дифференцировать по x и t. Иными словами, ряд (42) дает классическое решение НКЗ (3), (34), (35) и его можно исследовать “в лоб”.
Во многих физически важных случаях параметры НКЗ не удовлетворяют сформулированным выше достаточным условиям (входящие в задачу функции не обладают достаточной гладкостью). Тем не менее, метод Фурье сохраняет свое значение, ряд (42) дает обобщенное решение задачи. В дальнейшем наша цель – изучить применение метода Фурье к решению задач различных типов и возникающие при этом ряды; вопросы сходимости рядов к классическому решению задачи обсуждаться не будут.
Физическая интерпретация метода Фурье: гармоники и стоячие волны. Преобразуем выражения для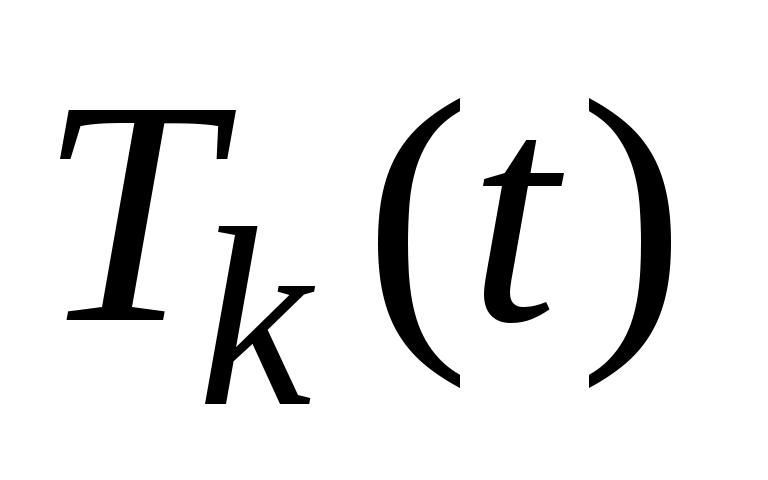 , введя амплитуды
, введя амплитуды 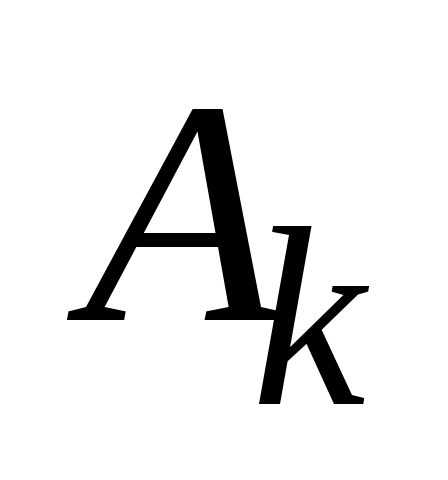 и начальные фазы
и начальные фазы 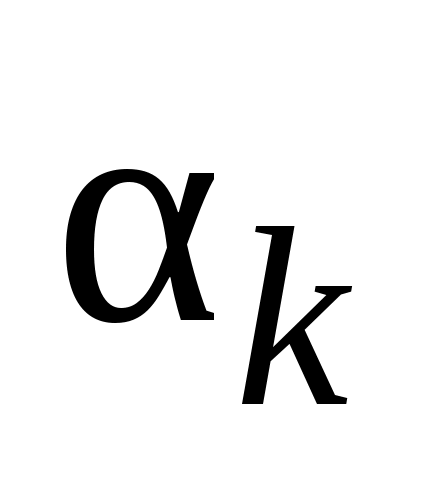 гармонических колебаний:
гармонических колебаний:
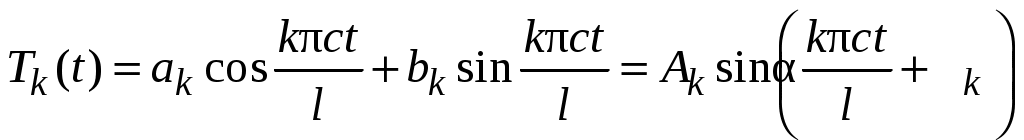 ,
,
где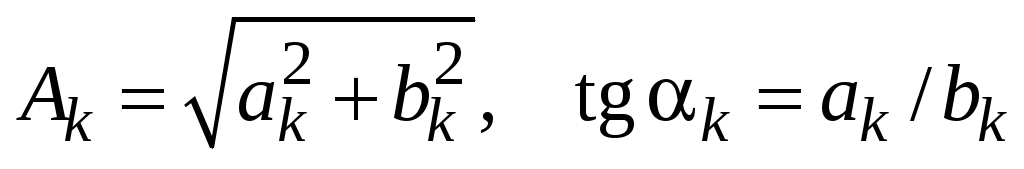 ; тогда ряд (42) принимает вид суммы гармоник:
; тогда ряд (42) принимает вид суммы гармоник:
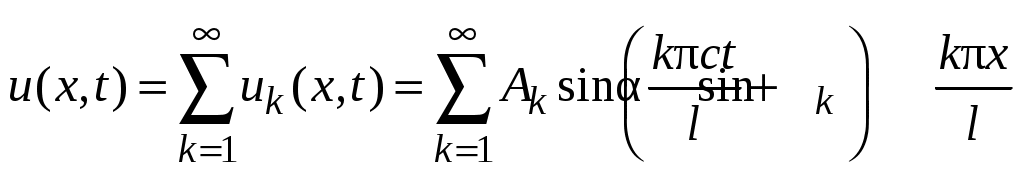 .
.
Каждый член этого ряда описывает стоячую волну, в которой точки струны совершают гармонические колебания с одинаковой фазой и с амплитудой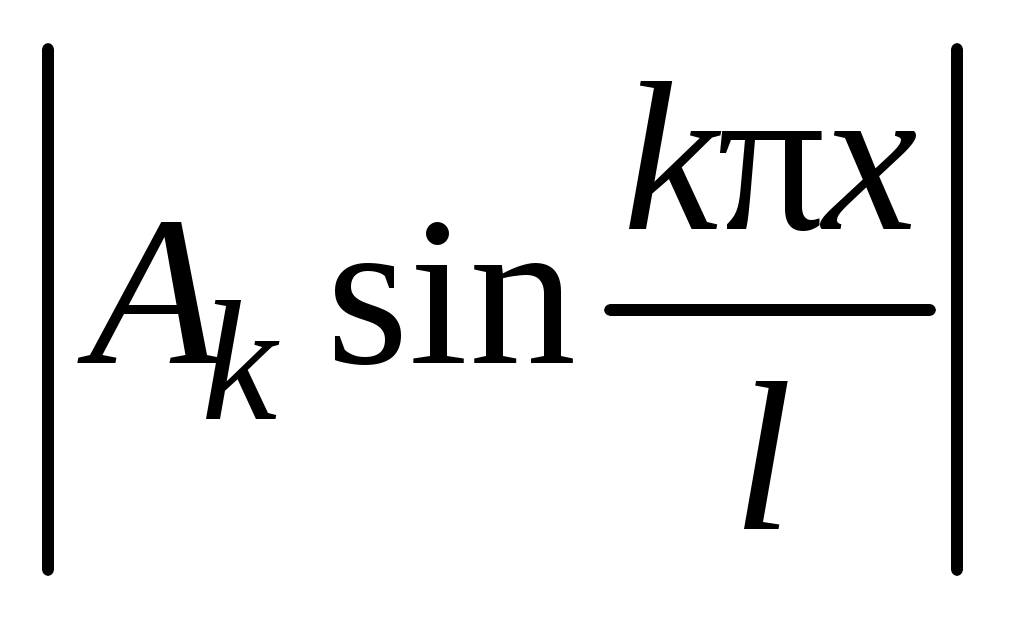 , зависящей от точки. При таком колебании струна издает звук, высота звука зависит от частоты колебаний
, зависящей от точки. При таком колебании струна издает звук, высота звука зависит от частоты колебаний 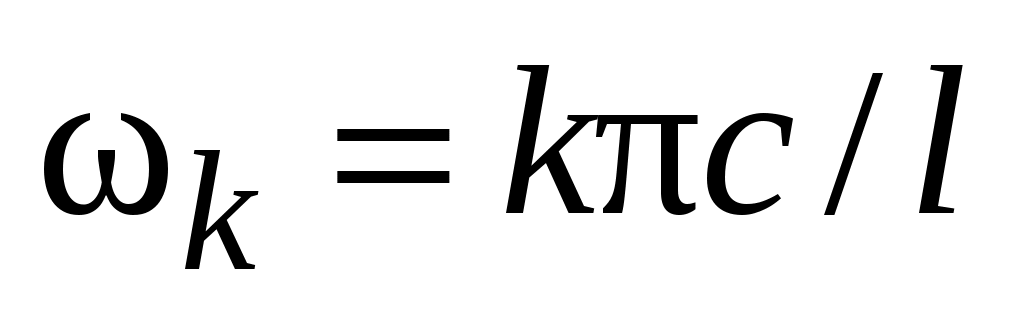 ,
,  , эти частоты называются собственными для данной струны. Звук, соответствующий наименьшей частоте,
, эти частоты называются собственными для данной струны. Звук, соответствующий наименьшей частоте, 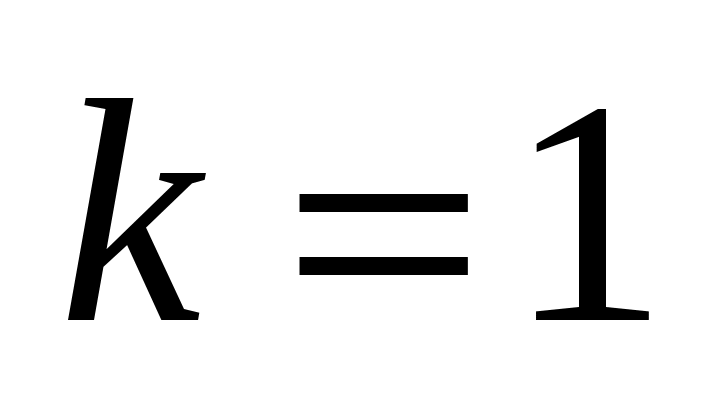 , называется основным тоном струны, остальные гармоники образуют набор обертонов.
, называется основным тоном струны, остальные гармоники образуют набор обертонов.
Таким образом, решение складывается из основного тона струны и набора обертонов. Амплитуды
складывается из основного тона струны и набора обертонов. Амплитуды  быстро убывают с ростом k, поэтому влияние обертонов на звук сводится к созданию тембра звука, различного для различных музыкальных инструментов и объясняемого именно наличием обертонов.
быстро убывают с ростом k, поэтому влияние обертонов на звук сводится к созданию тембра звука, различного для различных музыкальных инструментов и объясняемого именно наличием обертонов.
На рис.10 показаны положения струны в различные моменты времени, соответствующие двум первым гармоникам. Амплитуда колебаний k-й гармоники обращается в нуль в точках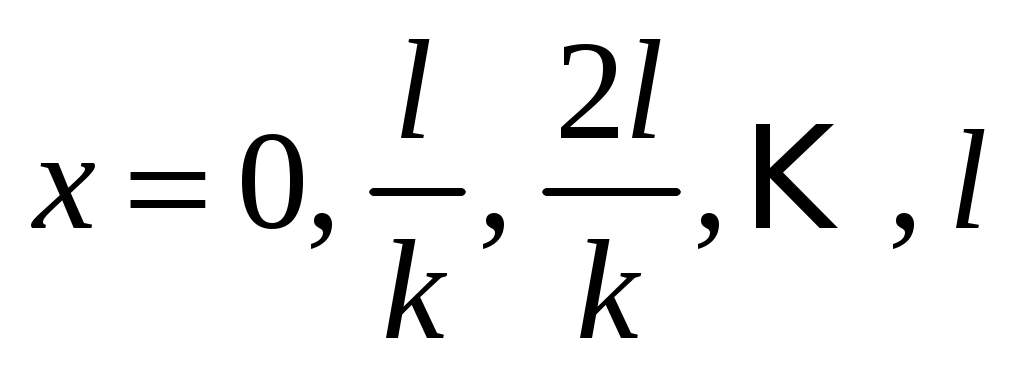 . Эти точки называются узлами k-й гармоники; точки
. Эти точки называются узлами k-й гармоники; точки 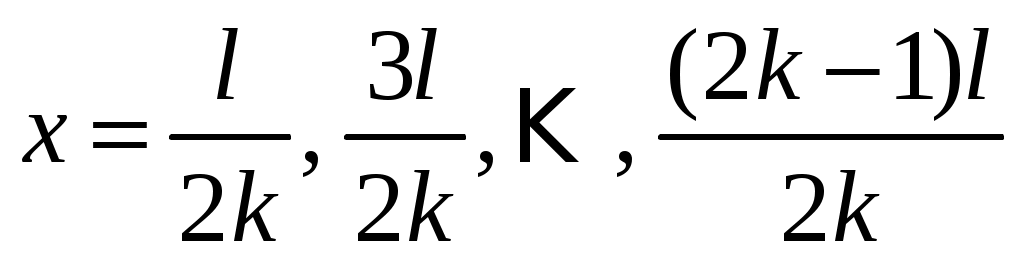 , в которых амплитуда достигает наибольшей величины, называются пучностями. Если в струне возбуждена только k-я гармоника, струна колеблется так, как если бы состояла из k отдельных кусков, закрепленных в узлах. Если прижать струну посередине, в пучности ее основного тона, то обратятся в нуль амплитуды основного тона и всех остальных нечетных гармоник, при этом четные гармоники останутся без изменения. В результате вместо своего обычного звука струна будет издавать звук с вдвое большей частотой, т.е. на октаву выше.
, в которых амплитуда достигает наибольшей величины, называются пучностями. Если в струне возбуждена только k-я гармоника, струна колеблется так, как если бы состояла из k отдельных кусков, закрепленных в узлах. Если прижать струну посередине, в пучности ее основного тона, то обратятся в нуль амплитуды основного тона и всех остальных нечетных гармоник, при этом четные гармоники останутся без изменения. В результате вместо своего обычного звука струна будет издавать звук с вдвое большей частотой, т.е. на октаву выше.
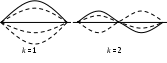
Рис.10
Постановка задачи. Колебания струны под действием распределенной силы описываются неоднородным уравнением (2). Ниже метод Фурье применяется к решению НКЗ (2), (34), (35), рассматриваются вынужденные колебания струны с двумя закрепленными концами. Случаи других однородных ГУ (два свободных конца или смешанные ГУ) исследуются аналогично.
Функцию , удовлетворяющую НКЗ
, удовлетворяющую НКЗ
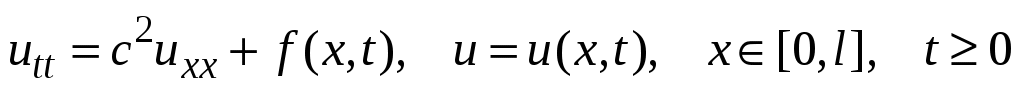 ,
,
 ;
;  ,
,
можно представить в виде суммы решений двух более простых задач: , где
, где  - решение НКЗ (3), (34), (35), описывающее свободные колебания струны, которые возникают вследствие заданного начального возмущения. Функция
- решение НКЗ (3), (34), (35), описывающее свободные колебания струны, которые возникают вследствие заданного начального возмущения. Функция  описывает чисто вынужденные колебания, т.е. колебания под действием силы
описывает чисто вынужденные колебания, т.е. колебания под действием силы  при условии, что в начальный момент струна покоилась. Для функции
при условии, что в начальный момент струна покоилась. Для функции  получено решение в виде ряда (42); необходимо определить
получено решение в виде ряда (42); необходимо определить  .
.
Решение НКЗ о чисто вынужденных колебаниях струны. Функция удовлетворяет задаче (44):
удовлетворяет задаче (44):
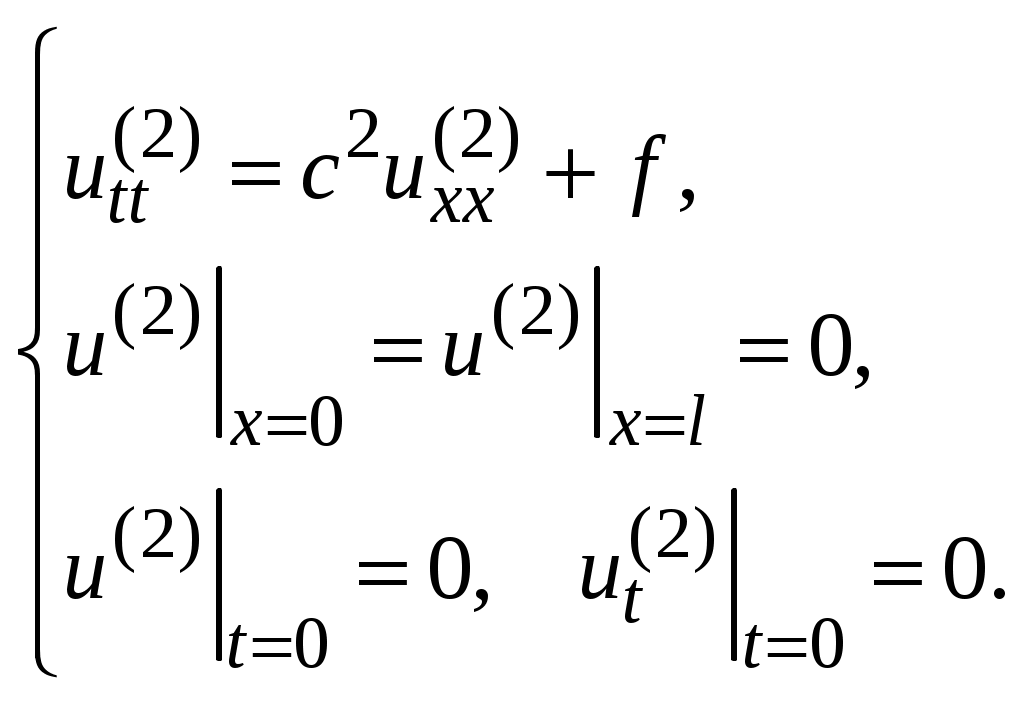 (44)
(44)
Будем искать ее в виде ряда
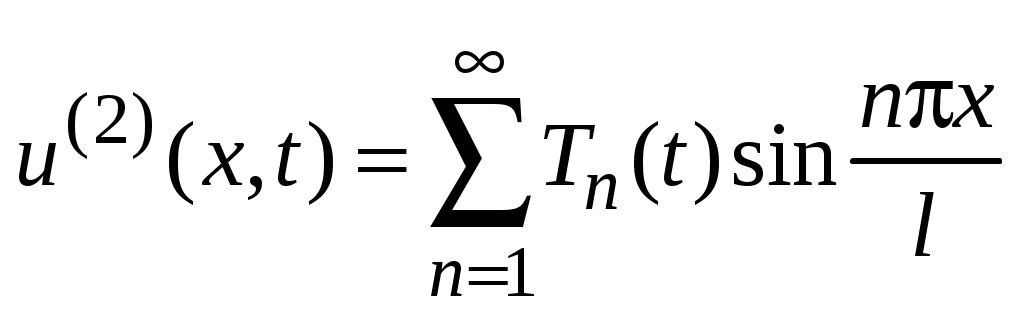 , (45)
, (45)
при этом ГУ для
где
Найденные значения
В результате получен счетный набор частных (линейно независимых) решений уравнения (3), удовлетворяющих ГУ (35):
Переобозначим произвольные постоянные: заменим
Благодаря линейности и однородности уравнения (3) и ГУ (35), любая линейная комбинация функций
Сумма ряда
Написанные ряды представляют собой разложения заданных функций
Ряд (42) с коэффициентами (43) формально удовлетворяет всем условиям поставленной задачи (3), (34), (35).
Нетрудно проверить, что решение в виде ряда совпадает с тем, которое было получено в § 5 методом отражений. При применении формулы Даламбера к ограниченной струне с закрепленными концами мы продолжали функции
Упражнение 11. Разложить продолженные функции
Упражнение 12. Решить методом Фурье задачу о свободных колебаниях ограниченной струны с двумя свободными концами и одним закрепленным, а другим свободным концом.
Об оправдании метода Фурье. Формально ряд (42) удовлетворяет уравнению и всем дополнительным условиям поставленной НКЗ. Возникает важный вопрос: при каких условиях на функции
,
Во многих физически важных случаях параметры НКЗ не удовлетворяют сформулированным выше достаточным условиям (входящие в задачу функции не обладают достаточной гладкостью). Тем не менее, метод Фурье сохраняет свое значение, ряд (42) дает обобщенное решение задачи. В дальнейшем наша цель – изучить применение метода Фурье к решению задач различных типов и возникающие при этом ряды; вопросы сходимости рядов к классическому решению задачи обсуждаться не будут.
Физическая интерпретация метода Фурье: гармоники и стоячие волны. Преобразуем выражения для
где
Каждый член этого ряда описывает стоячую волну, в которой точки струны совершают гармонические колебания с одинаковой фазой и с амплитудой
Таким образом, решение
На рис.10 показаны положения струны в различные моменты времени, соответствующие двум первым гармоникам. Амплитуда колебаний k-й гармоники обращается в нуль в точках

Рис.10
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных)
Постановка задачи. Колебания струны под действием распределенной силы описываются неоднородным уравнением (2). Ниже метод Фурье применяется к решению НКЗ (2), (34), (35), рассматриваются вынужденные колебания струны с двумя закрепленными концами. Случаи других однородных ГУ (два свободных конца или смешанные ГУ) исследуются аналогично.
Функцию
можно представить в виде суммы решений двух более простых задач:
Решение НКЗ о чисто вынужденных колебаниях струны. Функция
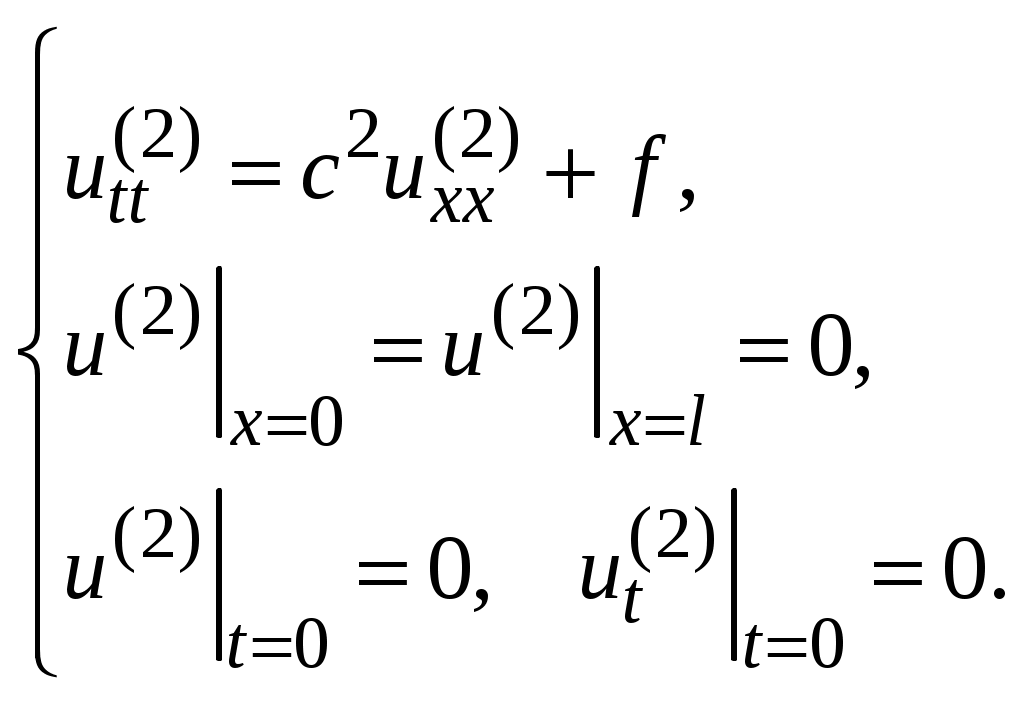 (44)
(44)Будем искать ее в виде ряда
при этом ГУ для