Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 387
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
.
Параметрический резонанс опаснее обычного.
4)Автоколебания .А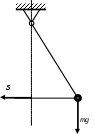 втоколебания или самоколебания – это незатухающиеся колебания, поддерживающиеся внешними силами. Характер этого воздействия определяется самим колебательным процессом, т.е. силы управляются самим движением системы (т.е. от движения системы зависит воздействие). На рисунке представлен кинематический пример: маятник с трением.
втоколебания или самоколебания – это незатухающиеся колебания, поддерживающиеся внешними силами. Характер этого воздействия определяется самим колебательным процессом, т.е. силы управляются самим движением системы (т.е. от движения системы зависит воздействие). На рисунке представлен кинематический пример: маятник с трением.
Вид уравнения:
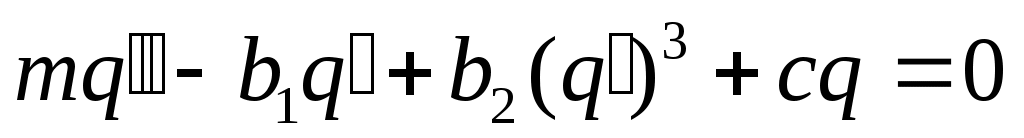 .
.
Эти 4 случая настолько самостоятельные, что это принципиально разные задачи.
15.4.2. Установившиеся вынужденные колебания системы с одной степенью свободы
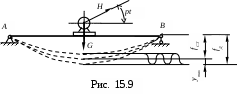
Простейшая схема возникновения в инженерной практике вынужденных колебаний представлена на рис. 15.9 . На балке АВ установлен двигатель весом G. Под действием этого груза балка изогнулась, и её максимальный статический прогиб равен
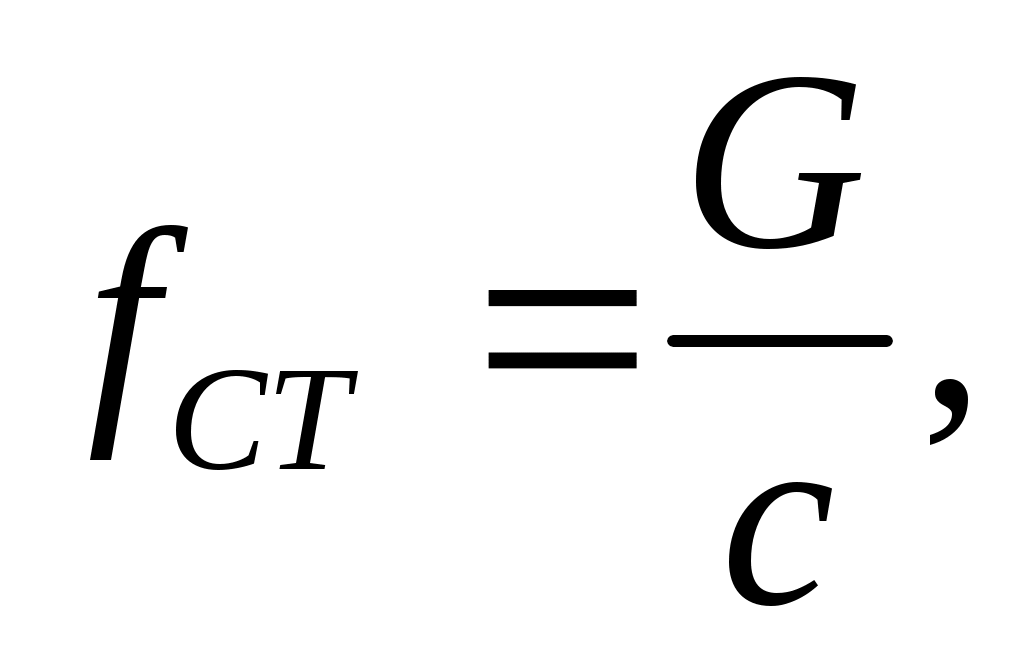
где с – изгибная жесткость конструкции; например, для балки на двух опорах, нагруженной посредине:
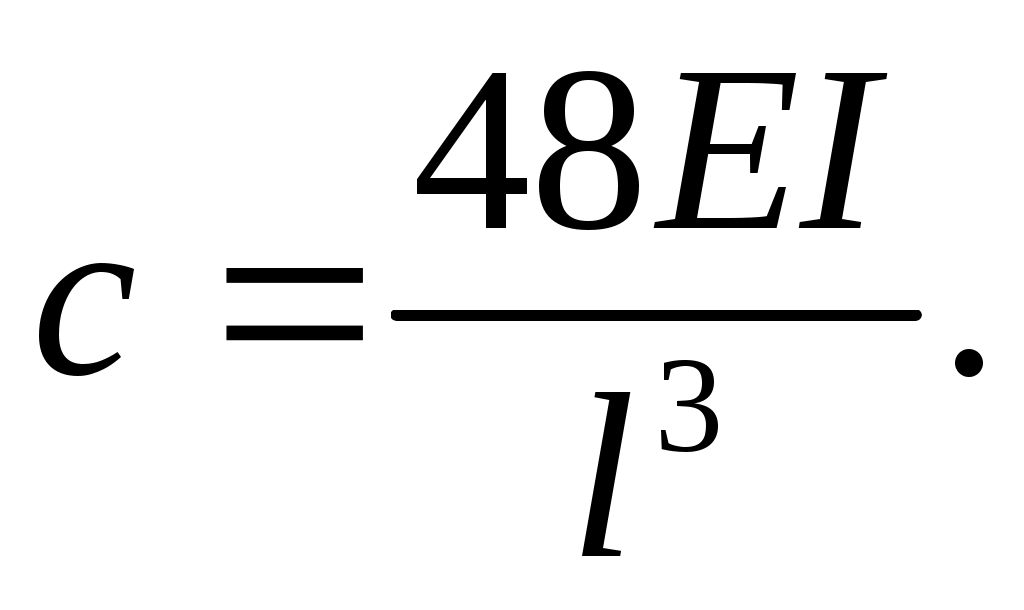
После пуска двигателя возникают колебания из-за неуравновешенности деталей двигателя.
Дифференциальное уравнение этого движения имеет вид

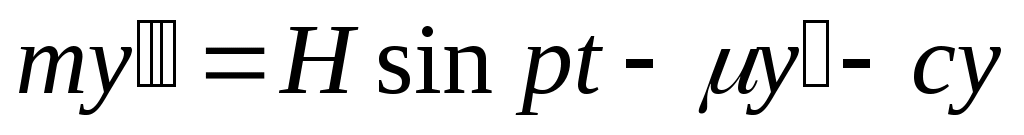 .
.
Перенося члены cy иy’ в левую часть равенства и разделив уравнение на m, получим
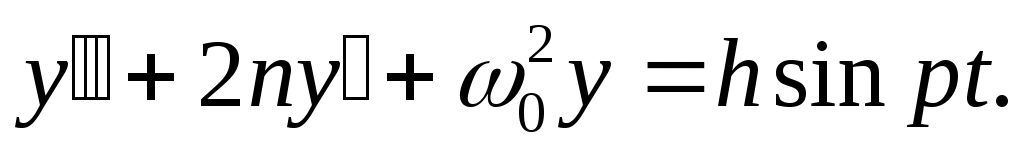 (15.10)
(15.10)
Рассмотрим коэффициенты уравнения.
Здесь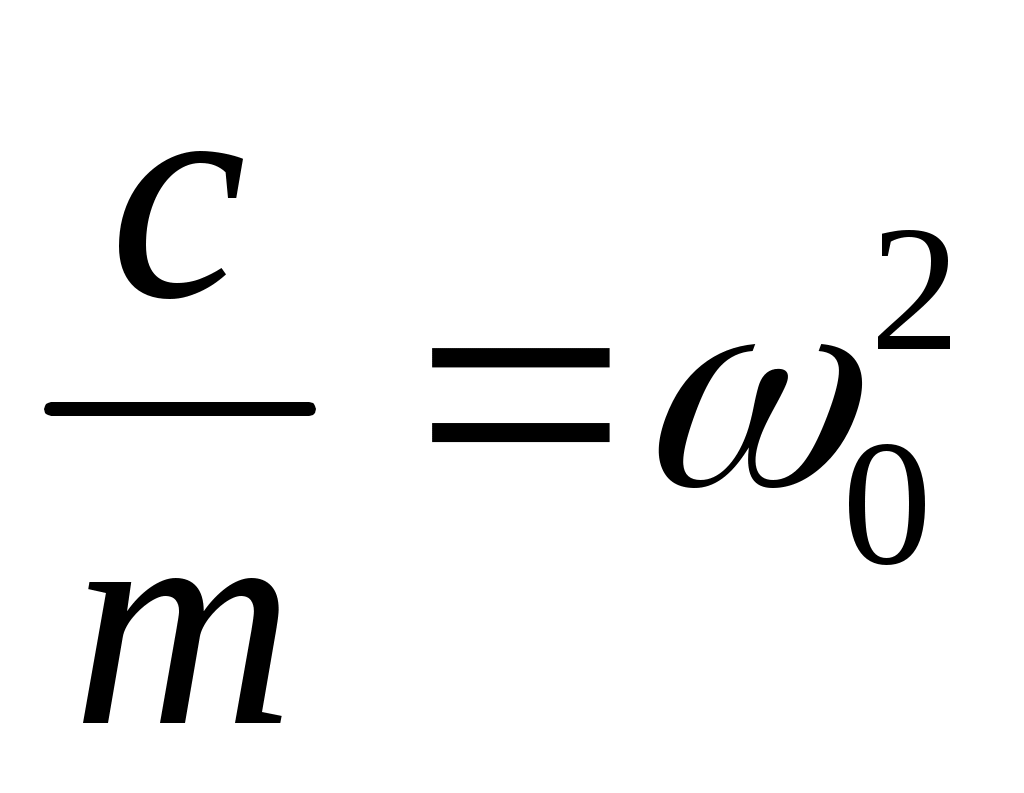 - квадрат частоты свободных колебаний;
- квадрат частоты свободных колебаний;
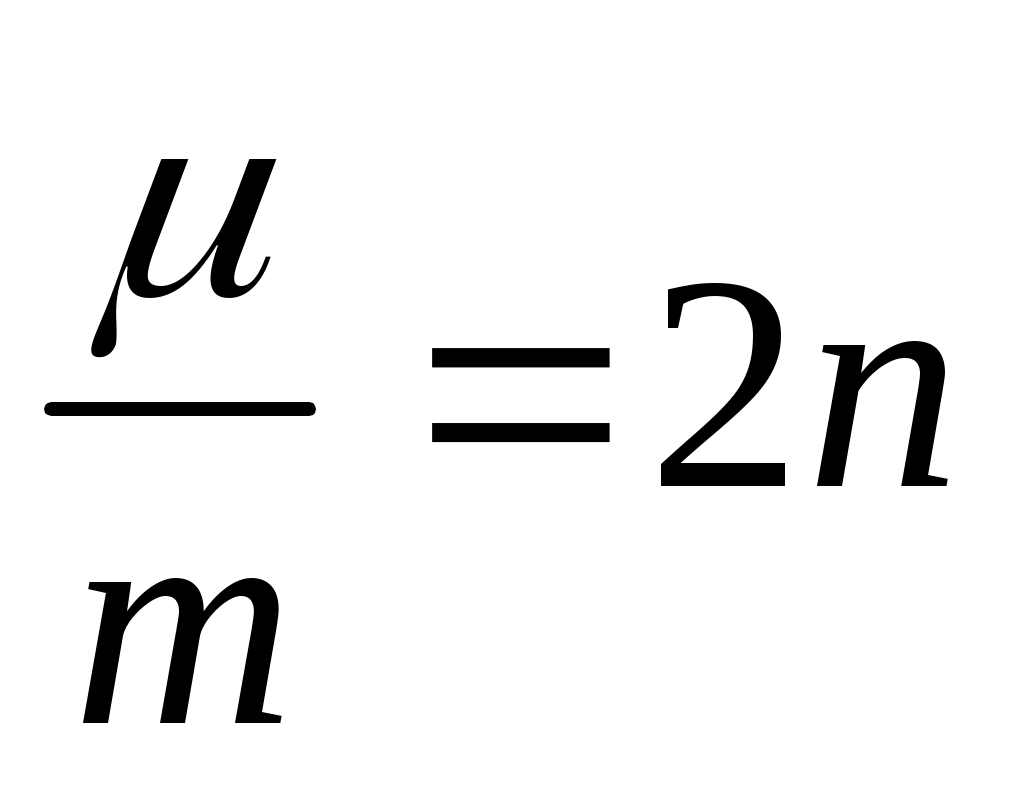 , где n – коэффициент затухания;
, где n – коэффициент затухания;
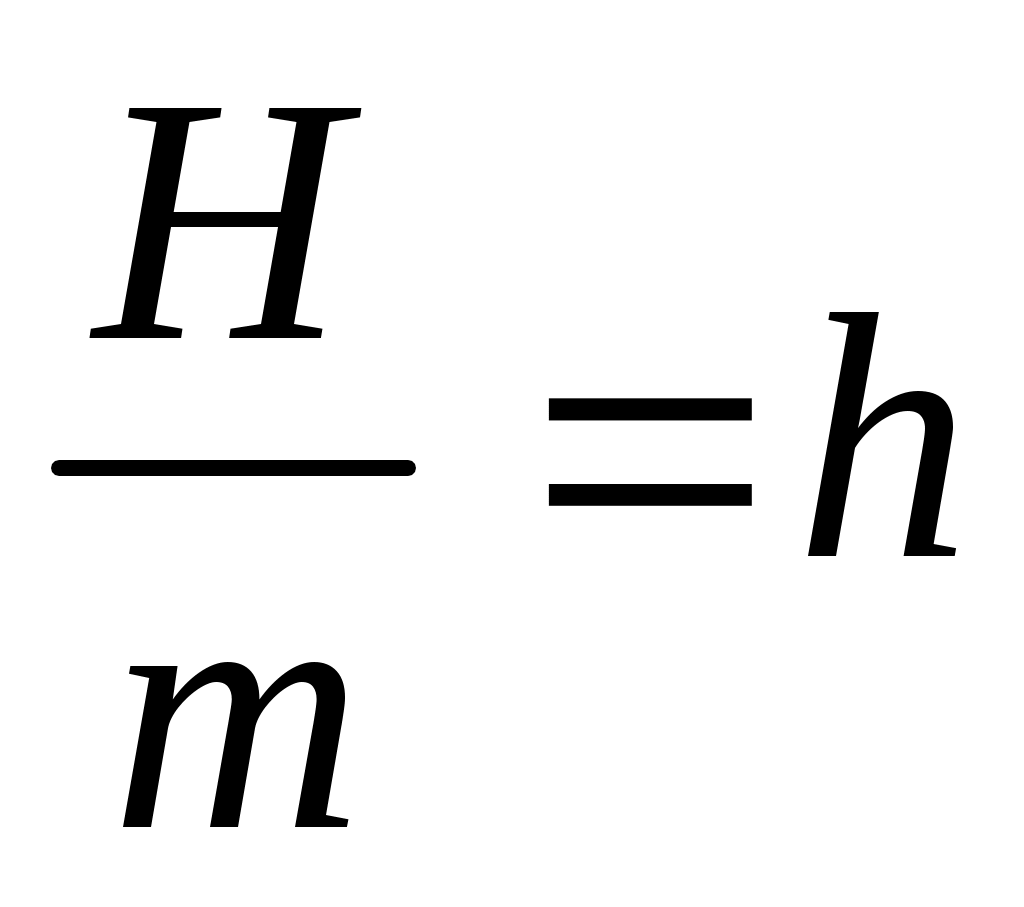 - отношение амплитуды возмущающей силы к сосредоточенной массе.
- отношение амплитуды возмущающей силы к сосредоточенной массе.
Уравнение (а) представляет собой дифференциальное уравнение вынужденных колебаний при наличии сопротивления движению, пропорционального скорости.
Общее решение уравнения (а) состоит из общего решения и частного
y=y1 + y2 . (15.11)
При 0 >n
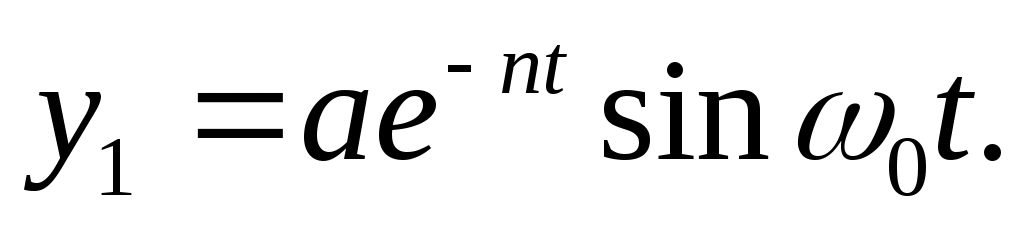
Наличие множителя e-nt , соответствует быстро затухающим колебаниям.
Поэтому через малый промежуток после начало движения устанавливается режим из собственно вынужденных колебаний, определяемых уравнением:
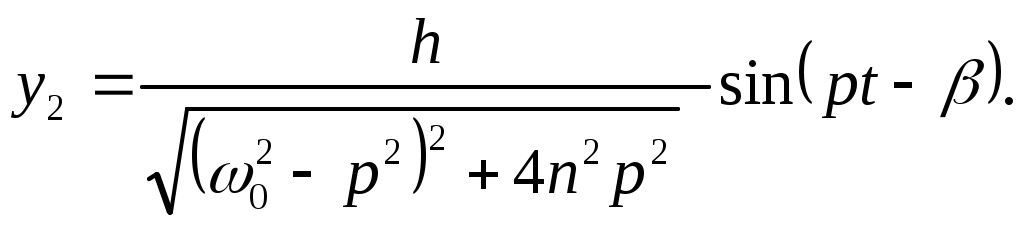
Для установления зависимости между амплитудой вынужденных колебаний и частотой вынуждающей силы (p) воспользуемся коэффициентом нарастания колебаний:
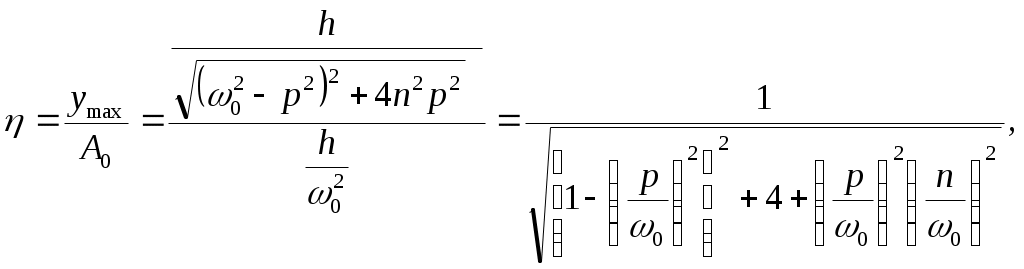 (15.12)
(15.12)
где А0 – перемещение, которое возникло бы при статическом действии максимального значения возмущающей силы Н, т.е.
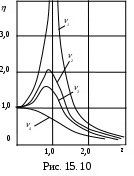
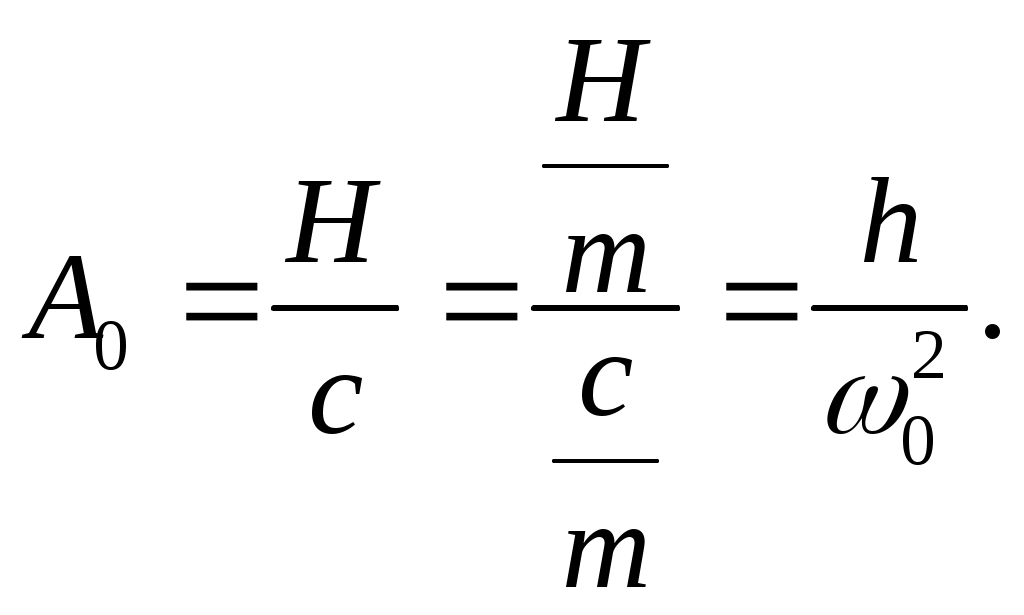
Окончательно (15.12) примет вид: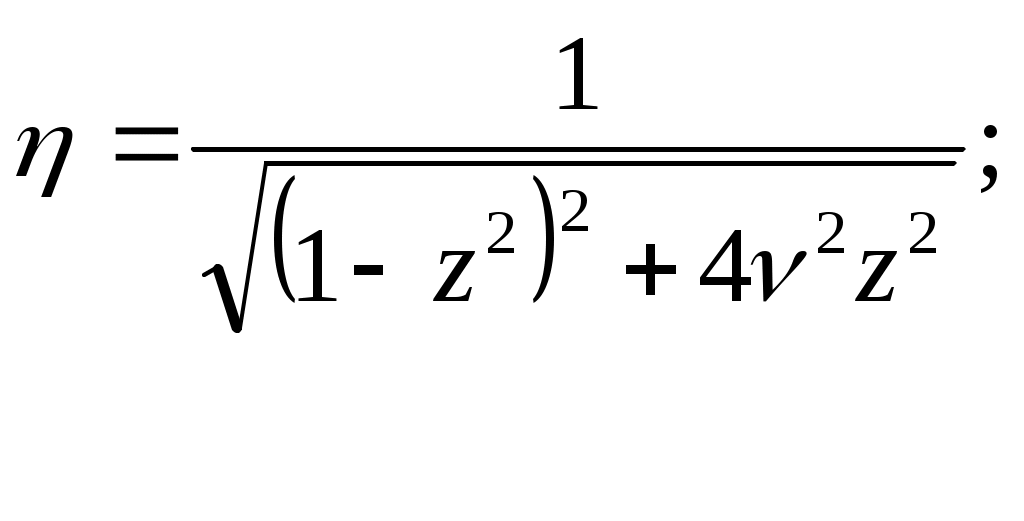 (15.13)
(15.13)
где z – коэффициент расстройки;
0 - частота собственных свободных колебаний;
- коэффициент демпфирования.
Для данной задачи
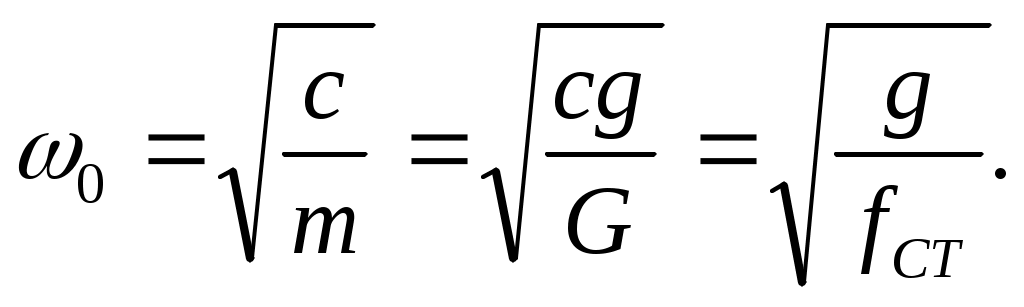 (15.14)
(15.14)
На рис. 15.10 построены кривые, каждая из которых представляет собой зависимость от z =р/0 при определенном значении = n /0 , где4>3>2>1.
При отсутствии сопротивления явление резонанса выражается в стремлении амплитуды вынужденных колебаний к бесконечности.
Если коэффициент расстройки z < 0,90 или z >1,10, то вместо формулы (15.13) можно вычислять по приближенной формуле
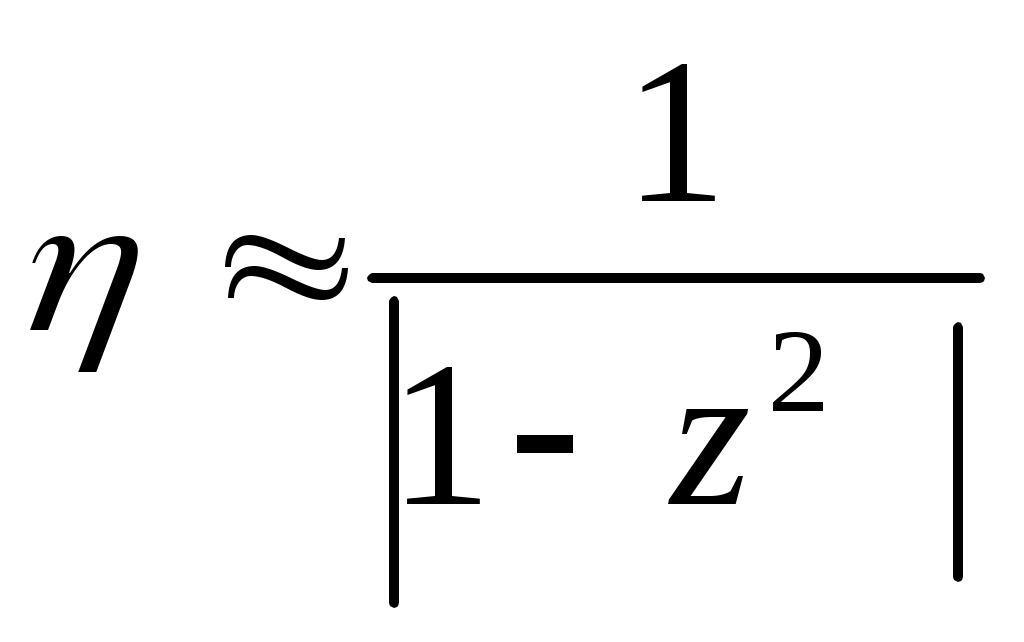 , (15.15)
, (15.15)
которое получается из формулы (15.13) при =0.
Зная коэффициент , находим наибольшую деформацию
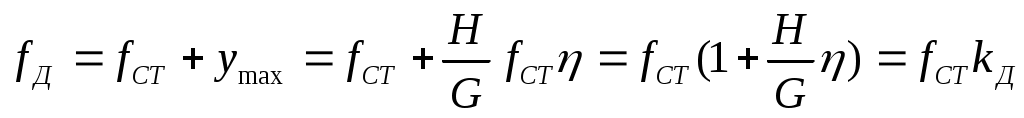 . (15.16)
. (15.16)
Величина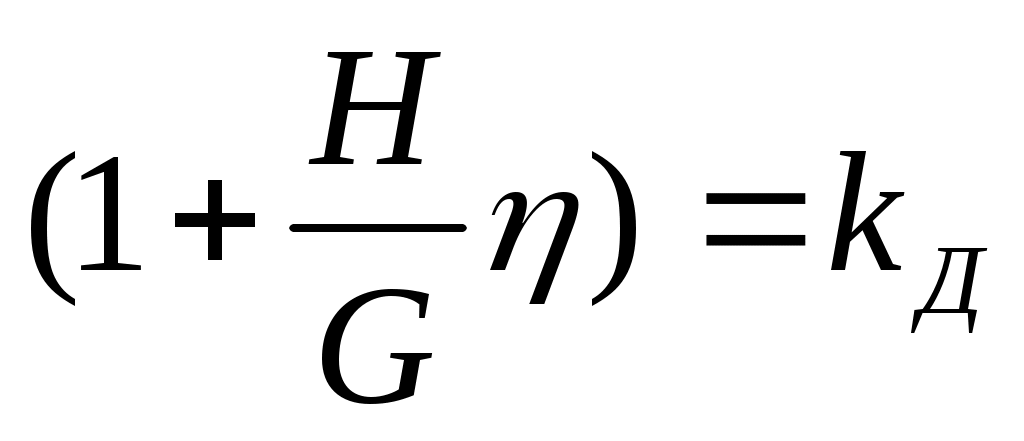 - динамический коэффициент для данной задачи.
- динамический коэффициент для данной задачи.
Предполагая, что явление протекает в пределах пропорциональности, получим формулу для проверки прочности:
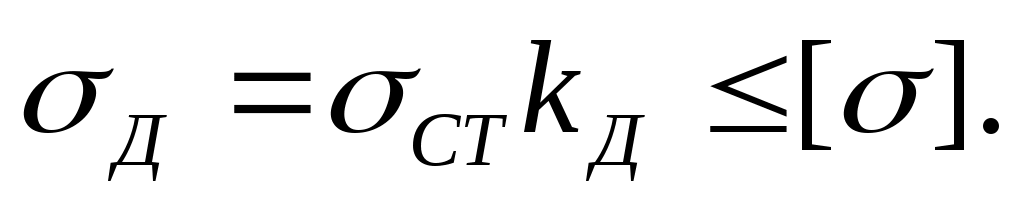 (15.17)
(15.17)
Вопросы для самопроверки
16. Прочность материалов при напряжениях,
периодически меняющихся во времени
16.1. Понятие об усталостном разрушении и его причины
С появлением первых машин практика эксплуатации их показала, что под действием циклически меняющихся напряжений материал разрушается при более низких напряжениях, чем при действии постоянных во времени нагрузок.
Как правило, детали разрушались без видимых остаточных деформаций даже в тех случаях, когда они изготовлялись из пластических материалов. Возникло предположение, что под влиянием переменных напряжений материал с течением времени постепенно перерождается, как бы «устает», и вместо пластического становится хрупким.
Позднее, с усовершенствованием лабораторных методов исследования было установлено, что структура и механические свойства материала от переменных напряжений не меняется, название «усталость» материалов, хотя оно и не отвечает физической природе явления, осталось и им повсюду пользуются и в настоящее время.
Существует много гипотез, объясняющих причины возникновения усталостных трещин. Наиболее удовлетворительное объяснение состоит в следующем. Металл, являясь поликристаллическим телом, состоит из кристаллов, разделенных прослойками, неметаллическими включениями и т.п.
Кристаллиты не являются однородными. Более или менее однородными можно считать только части кристаллитов – «зерна». Зерна одного и того же кристаллита обладают различной упругостью, пластичностью, прочностью. При нагрузках отдельные зерна испытывают различные напряжения по величине и по направлению. Некоторые из них оказываются пластически деформированные, хотя среднее напряжение по сечению может быть значительно меньше предела упругости. В отдельных неблагоприятно ориентированных зернах даже при небольших средних амплитудах напряжениях возникают: микротрещины, циклическое скольжение по плоскостям скольжения кристаллитов. Вследствие циклического скольжения возникает разрыхление, накопление дефектов, приводящих после определенного числа циклов к появлению трещины в одном или нескольких зернах. В последующем трещины объединяются в одну микроскопическую трещину, которая начинает развиваться. После того как трещина распространится на значительную часть сечения, происходит внезапное разрушение.
Таким образом, под усталостью в настоящее время понимают процесс постепенного накопления повреждений материала при действии переменных напряжений, приводящий к образованию трещин и разрушению.
Свойство материала противостоять усталости называется выносливостью.
16.2. Виды циклов напряжений
Р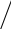 ассмотрим точку К, расположенную на контуре поперечного сечения вращающегося вала (см. рис 16.1).
ассмотрим точку К, расположенную на контуре поперечного сечения вращающегося вала (см. рис 16.1).
В
сечении m-mдействует изгибающий момент, от которого в точке К возникают нормальные напряжения
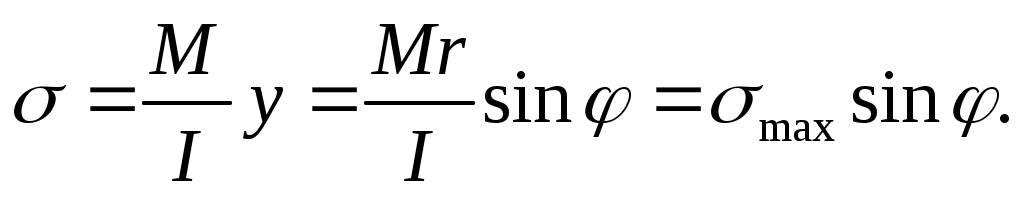 (16.1)
(16.1)
Угол изменяется по закону =t,
где - угловая скорость вращения. Следовательно,
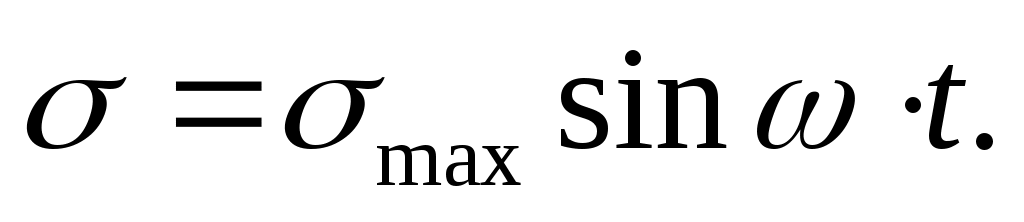 (16.2)
(16.2)
Наибольшее растягивающее напряжение max в точке К будут тогда, когда она займет положение точки 2 , а min будет в положении точки 4. Когда точка К на нейтральной оси (положения точек 1 и 3), напряжения в ней будут равны нулю ( =0 ).
По уравнению (16.2) построен график (см. рис. 16.2).
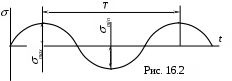
Как видим, напряжения изменяются во времени периодически. На практике графики переменных нагрузок во времени выглядят самым разнообразным образом. Однако та же практика показывает, что форма периодических колебаний практически не отражается на прочности конструкционных элементов, а все зависит от максимального max и минимального min напряжения в цикле. Поэтому в расчетной практике принято любой из этих графиков заменять синусоидой (рис. 16.3).
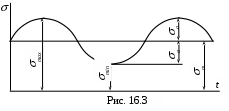
Более удобными в расчетах оказываются значения среднего и амплитудного напряжений цикла
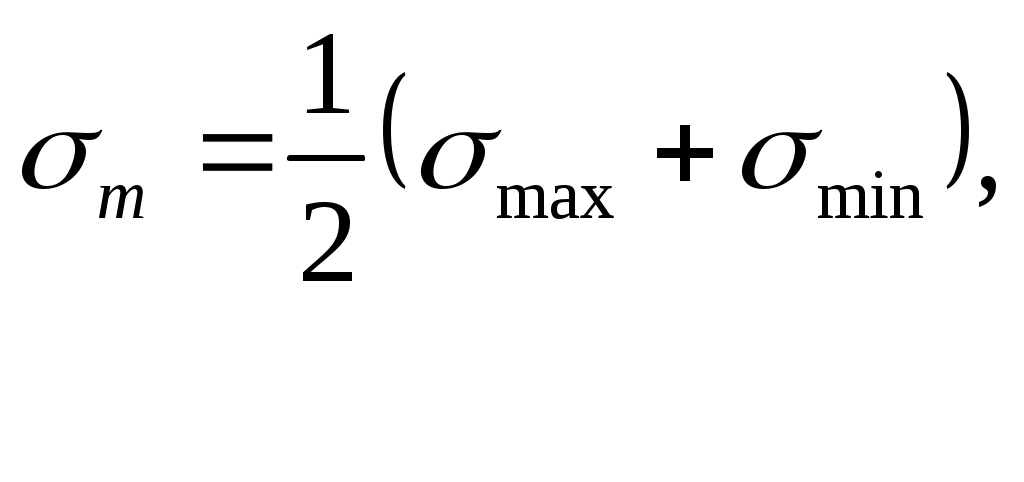 (16.3)
(16.3)
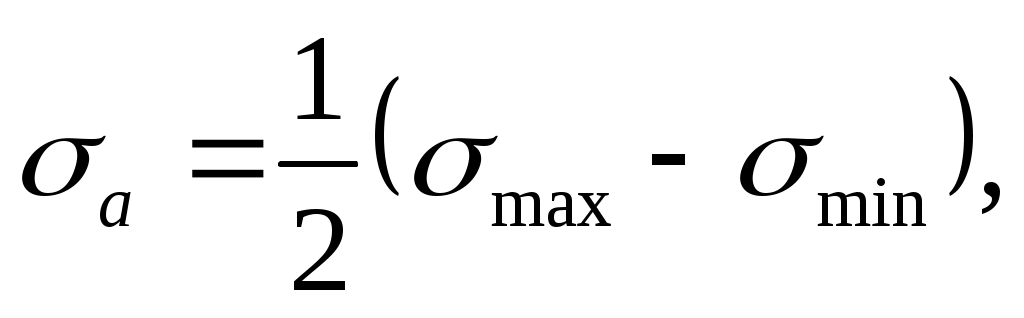 (16.4)
(16.4)
где m – среднее постоянное напряжение цикла;
а – амплитуда цикла – наибольшее значение переменной составляю- щей цикла напряжений.
Параметрический резонанс опаснее обычного.
4)Автоколебания .А
 втоколебания или самоколебания – это незатухающиеся колебания, поддерживающиеся внешними силами. Характер этого воздействия определяется самим колебательным процессом, т.е. силы управляются самим движением системы (т.е. от движения системы зависит воздействие). На рисунке представлен кинематический пример: маятник с трением.
втоколебания или самоколебания – это незатухающиеся колебания, поддерживающиеся внешними силами. Характер этого воздействия определяется самим колебательным процессом, т.е. силы управляются самим движением системы (т.е. от движения системы зависит воздействие). На рисунке представлен кинематический пример: маятник с трением.Вид уравнения:
Эти 4 случая настолько самостоятельные, что это принципиально разные задачи.
15.4.2. Установившиеся вынужденные колебания системы с одной степенью свободы
Простейшая схема возникновения в инженерной практике вынужденных колебаний представлена на рис. 15.9 . На балке АВ установлен двигатель весом G. Под действием этого груза балка изогнулась, и её максимальный статический прогиб равен
где с – изгибная жесткость конструкции; например, для балки на двух опорах, нагруженной посредине:

После пуска двигателя возникают колебания из-за неуравновешенности деталей двигателя.
Дифференциальное уравнение этого движения имеет вид
Перенося члены cy иy’ в левую часть равенства и разделив уравнение на m, получим
Рассмотрим коэффициенты уравнения.
Здесь
Уравнение (а) представляет собой дифференциальное уравнение вынужденных колебаний при наличии сопротивления движению, пропорционального скорости.
Общее решение уравнения (а) состоит из общего решения и частного
y=y1 + y2 . (15.11)
При 0 >n
Наличие множителя e-nt , соответствует быстро затухающим колебаниям.
Поэтому через малый промежуток после начало движения устанавливается режим из собственно вынужденных колебаний, определяемых уравнением:
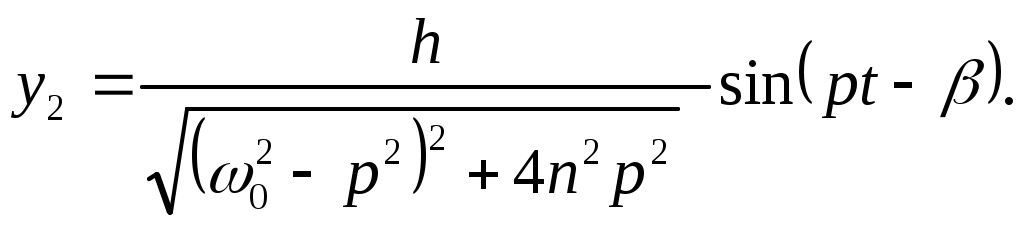
Для установления зависимости между амплитудой вынужденных колебаний и частотой вынуждающей силы (p) воспользуемся коэффициентом нарастания колебаний:
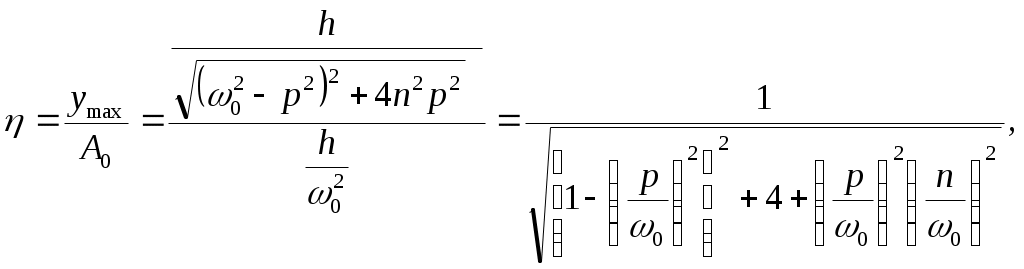 (15.12)
(15.12) где А0 – перемещение, которое возникло бы при статическом действии максимального значения возмущающей силы Н, т.е.

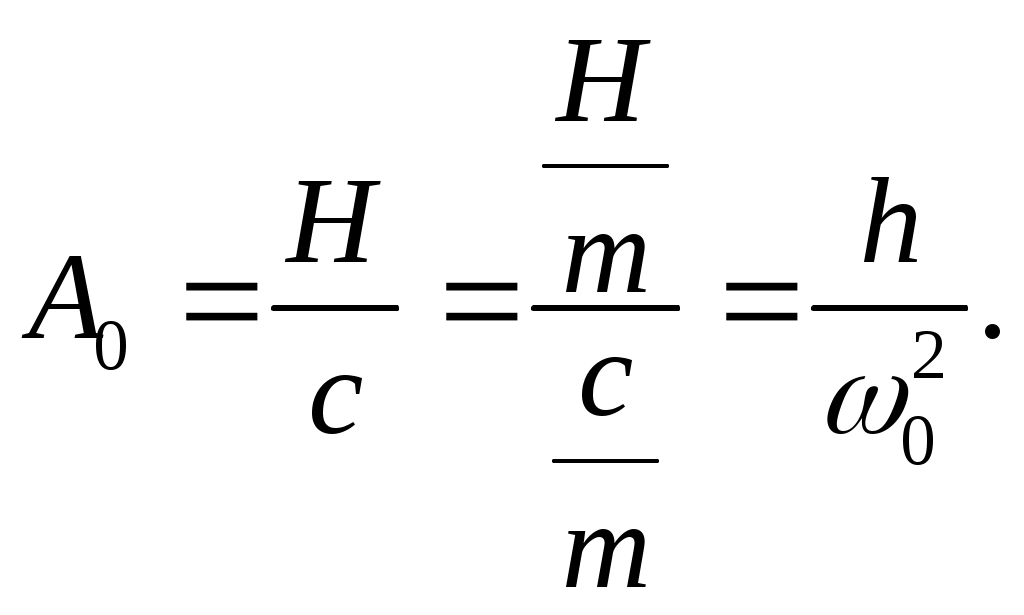
Окончательно (15.12) примет вид:
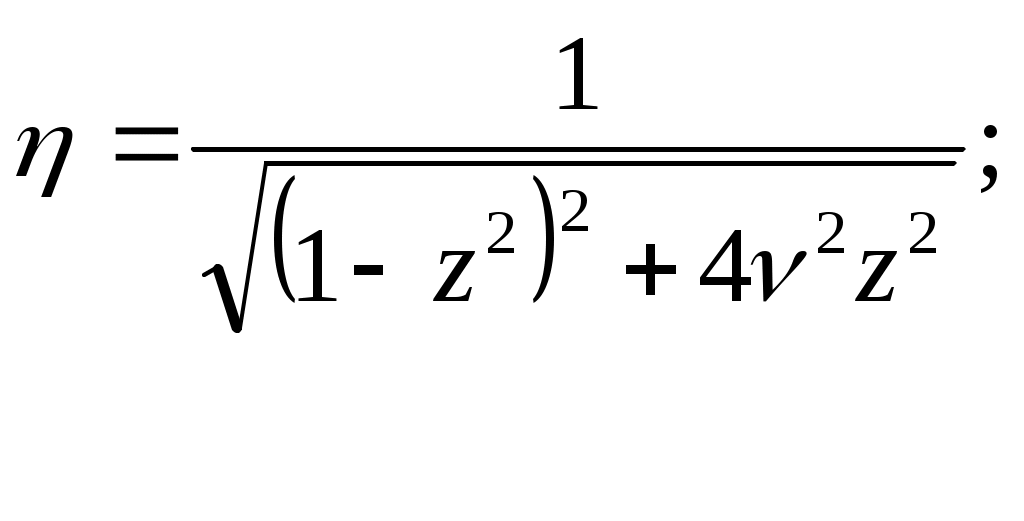 (15.13)
(15.13) где z – коэффициент расстройки;
0 - частота собственных свободных колебаний;
- коэффициент демпфирования.
Для данной задачи
На рис. 15.10 построены кривые, каждая из которых представляет собой зависимость от z =р/0 при определенном значении = n /0 , где4>3>2>1.
При отсутствии сопротивления явление резонанса выражается в стремлении амплитуды вынужденных колебаний к бесконечности.
Если коэффициент расстройки z < 0,90 или z >1,10, то вместо формулы (15.13) можно вычислять по приближенной формуле
которое получается из формулы (15.13) при =0.
Зная коэффициент , находим наибольшую деформацию
Величина
Предполагая, что явление протекает в пределах пропорциональности, получим формулу для проверки прочности:
Вопросы для самопроверки
-
Какие задачи сопротивления материалов требуют учета динамического характера нагрузки? -
В чем состоит общий прием решения задач с учетом сил инерции? -
Что называется динамическим коэффициентом? -
Какие допущения положены в основу технической теории удара? -
Как определяется приведенная масса (вес) стержня? -
Как вычисляют динамический коэффициент? -
Какие виды колебаний системы с одной степенью свободы? -
Когда наблюдаются установившиеся вынужденные колебания системы с одной степенью свободы? -
Как вычисляется коэффициентом нарастания колебаний? -
Что такое коэффициенты: расстройки, демпфирования? -
В какой области частот можно определять коэффициент нарастания колебаний? -
Как вычисляется динамический коэффициент при установившихся вынужденных колебания системы с одной степенью свободы? -
Как определяются напряжения, какой фактор влияет на их величину?
16. Прочность материалов при напряжениях,
периодически меняющихся во времени
16.1. Понятие об усталостном разрушении и его причины
С появлением первых машин практика эксплуатации их показала, что под действием циклически меняющихся напряжений материал разрушается при более низких напряжениях, чем при действии постоянных во времени нагрузок.
Как правило, детали разрушались без видимых остаточных деформаций даже в тех случаях, когда они изготовлялись из пластических материалов. Возникло предположение, что под влиянием переменных напряжений материал с течением времени постепенно перерождается, как бы «устает», и вместо пластического становится хрупким.
Позднее, с усовершенствованием лабораторных методов исследования было установлено, что структура и механические свойства материала от переменных напряжений не меняется, название «усталость» материалов, хотя оно и не отвечает физической природе явления, осталось и им повсюду пользуются и в настоящее время.
Существует много гипотез, объясняющих причины возникновения усталостных трещин. Наиболее удовлетворительное объяснение состоит в следующем. Металл, являясь поликристаллическим телом, состоит из кристаллов, разделенных прослойками, неметаллическими включениями и т.п.
Кристаллиты не являются однородными. Более или менее однородными можно считать только части кристаллитов – «зерна». Зерна одного и того же кристаллита обладают различной упругостью, пластичностью, прочностью. При нагрузках отдельные зерна испытывают различные напряжения по величине и по направлению. Некоторые из них оказываются пластически деформированные, хотя среднее напряжение по сечению может быть значительно меньше предела упругости. В отдельных неблагоприятно ориентированных зернах даже при небольших средних амплитудах напряжениях возникают: микротрещины, циклическое скольжение по плоскостям скольжения кристаллитов. Вследствие циклического скольжения возникает разрыхление, накопление дефектов, приводящих после определенного числа циклов к появлению трещины в одном или нескольких зернах. В последующем трещины объединяются в одну микроскопическую трещину, которая начинает развиваться. После того как трещина распространится на значительную часть сечения, происходит внезапное разрушение.
Таким образом, под усталостью в настоящее время понимают процесс постепенного накопления повреждений материала при действии переменных напряжений, приводящий к образованию трещин и разрушению.
Свойство материала противостоять усталости называется выносливостью.
16.2. Виды циклов напряжений
Р
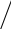 ассмотрим точку К, расположенную на контуре поперечного сечения вращающегося вала (см. рис 16.1).
ассмотрим точку К, расположенную на контуре поперечного сечения вращающегося вала (см. рис 16.1).В

сечении m-mдействует изгибающий момент, от которого в точке К возникают нормальные напряжения
Угол изменяется по закону =t,
где - угловая скорость вращения. Следовательно,
Наибольшее растягивающее напряжение max в точке К будут тогда, когда она займет положение точки 2 , а min будет в положении точки 4. Когда точка К на нейтральной оси (положения точек 1 и 3), напряжения в ней будут равны нулю ( =0 ).
По уравнению (16.2) построен график (см. рис. 16.2).

Как видим, напряжения изменяются во времени периодически. На практике графики переменных нагрузок во времени выглядят самым разнообразным образом. Однако та же практика показывает, что форма периодических колебаний практически не отражается на прочности конструкционных элементов, а все зависит от максимального max и минимального min напряжения в цикле. Поэтому в расчетной практике принято любой из этих графиков заменять синусоидой (рис. 16.3).

Более удобными в расчетах оказываются значения среднего и амплитудного напряжений цикла
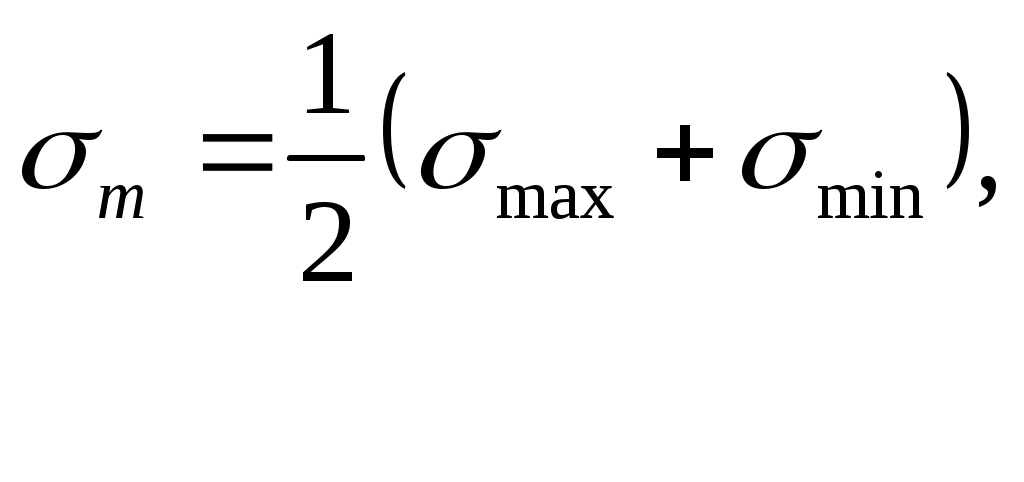 (16.3)
(16.3)где m – среднее постоянное напряжение цикла;
а – амплитуда цикла – наибольшее значение переменной составляю- щей цикла напряжений.