Файл: Александры Анатольевны.doc

По моему опыту работы, только после усвоения учащимися вопроса исследования квадратного уравнения есть смысл переходить к задаче: решить уравнение.

12. 
    Решить уравнение x² + 5ax + 4a² = 0.
    

Решение:

1. 
   Коэффициент при x²равен 1, следовательно, уравнение квадратное.
   
2. 
   Найдем дискриминант: D = (5a)² – 4 1 4a² = 25a² – 16a² = 9a².
   

а) При a 0, D 0: уравнение имеет два корня = 3a:

x_1,2 = .

(Комментарий: В этом месте решения возникает техническая сложность, связанная с раскрытием модуля. Несколько раз следует подробно записать нахождение корней.)

Если а  0, x₁ = = –4a, x₂ = = –a.

Если a  0, x₁ = = –a, x₂ = = –4a.

Т.е. при a 0 и a 0 корни уравнения выражаются через aодинаково.

б) При a = 0, D = 0: x = = = 0.

Ответ: при a  0 x₁ = –4a, x₂ = –a;

при a = 0 x = 0.

Комментарий: Ответ можно выписать, не выделяя случай a=0: при любых a x₁=–4a, x₂= –a; но я предпочитаю выделять случай равенства дискриминанта нулю, т.к. такая запись снимает вопрос о количестве корней в зависимости от a.

12. 
    Решить уравнение ax²+ 2x + 1 = 0.
    

Решение: Первоначально рассмотрим случай, когда первый коэффициент равен нулю.

1. 
   Если a = 0, 2x + 1 = 0, x = –0,5 , то уравнение линейное, имеет один корень.
   
2. 
   Если a 0, то имеем квадратное кравнение. Найдем D₁. D₁ = 1 – a.
   

---

а) ЕслиD₁  0, 1– a 0, a 1, a 0, уравнение имеет два корня:

x_1,2 = .

б) ЕслиD₁ = 0, a = 1, то уравнение имеет один корень: x = = –1.

в) ЕслиD₁  0, 1– a 0, a 1, то уравнение не имеет корней.

Ответ: при a 1,a 0 x_1,2 = ;

при a = 0 x = –0,5;

при a = 1 x = –1;

при a 1 корней нет.

Разбираем еще одно аналогичное уравнение (можно пригласить ученика к доске).

12. 
    ax² x + 3 = 0.
    

Ответ: при a ,a 0 x_1,2 = ;

при a = 0 x = 3;

при a = x = 6;

при a корней нет.

12. 
    (a + 1)x² 2x + 1 a = 0.
    

Теперь учащиеся готовы к составлению алгоритма.

Алгоритм решения квадратных уравнений с параметрами.

Ax² + Bx + C = 0

1. 
   Несколько раз прочитать формулировку задачи. Выяснить, зависит ли степень уравнения от параметра. Если требуется, найти ОДЗ параметра.
   
2. 
   Найти значения параметра, при которых A = 0. Решить линейное уравнение.
   
3. 
   Решить квадратное уравнение.
   

а) Определить, при каких значениях параметра D 0. Найти корни по формуле x_1,2 = .

б) Определить, при каких значениях параметра D = 0. Найти корень по формуле x = .

в) Определить, при каких значениях параметра D 0, корней нет.

4. 
   Исключить из п. 3 а), б), в) значения параметра из п. 1, 2.
   
5. 
   Записать ответ.
   

---

---

Образец оформления.

12. 
    Решить уравнение a (a + 3)x²+ (2a + 6)x  3a  9 = 0.
    

Решение:

1. 
   a(a + 3) = 0 при a = 0, a = –3.
   

а) Еслиa = 0, получим 6x – 9 = 0,

6x = 9,

x = 1,5.

б) Еслиa = –3, получим 0x + 9 – 9 = 0,

0 x = 0,

x – любое число.

2. 
   a(a + 3)  0 при a  0, a  –3.
   

a (a + 3)x²+ 2(a + 2)x  3(a + 3) = 0.

Разделим обе части уравнения на a + 3  0, получим

ax² + 2x  3 = 0, D₁ = 1 + 3a.

а) D₁  0, если 1 + 3a  0, a  , a  0.

Уравнение имеет два корня:

x_1,2 = .

б) D₁ = 0, если 1 + 3a = 0, a =  .

Уравнение имеет один корень:

x = = 3.

в) D₁  0, если 1 + 3a  0, a  , a 3.

Уравнение не имеет корней.

Ответ: при a ,a3 корней нет;

при a = –3 x – любое число;

при a  , a  0 x_1,2 = ;

при a =  , x = 3;

при a = 0, x = 1,5.

Комментарий: Довольно часто запись ответа вызывает затруднения. Вот один из возможных способов действий, использующий ось параметра a:

1. 
   Нанести на ось параметра a все значения, которые "встретились" при решении;
   
2. 
   Указать значения (или число) корней в каждом промежутке и отдельных точках.
   

---

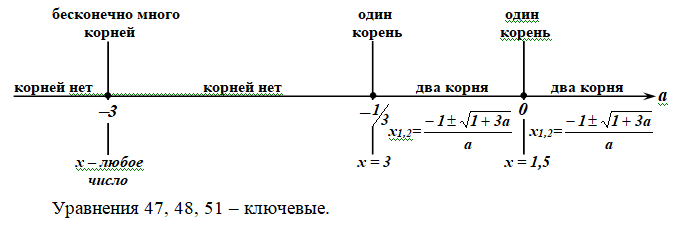
Задачи для отработки.

12. 
    Решите уравнение.
    

а) x² 3ax + 2a² = 0;б) x² bx  2b² = 0;в) x²+ 5bx  6b² = 0.

12. 
    а) x² (2a  4)x  8a = 0; б) x² + (3b  2)x  6b = 0; в) x² (3a  2)x + 2a² a  3 = 0; г) x² 4bx + 3b² 4b  4 = 0.
    
13. 
    а) ax² (a + 1)x + 1 = 0;б) mx² 6x + 1 = 0.
    

Выбор задач ограничен тем, что восьмиклассники не умеют решать квадратные неравенства.

Желательно на этом этапе провести проверочную работу, в которую включить задания типа 37, 39, 47, 48.

При наличии времени можно рассмотреть три интересные задачи, решение которых усложнено рассмотрением области допустимых значений параметра и неизвестного.

12. 
    Решить относительно x:  = .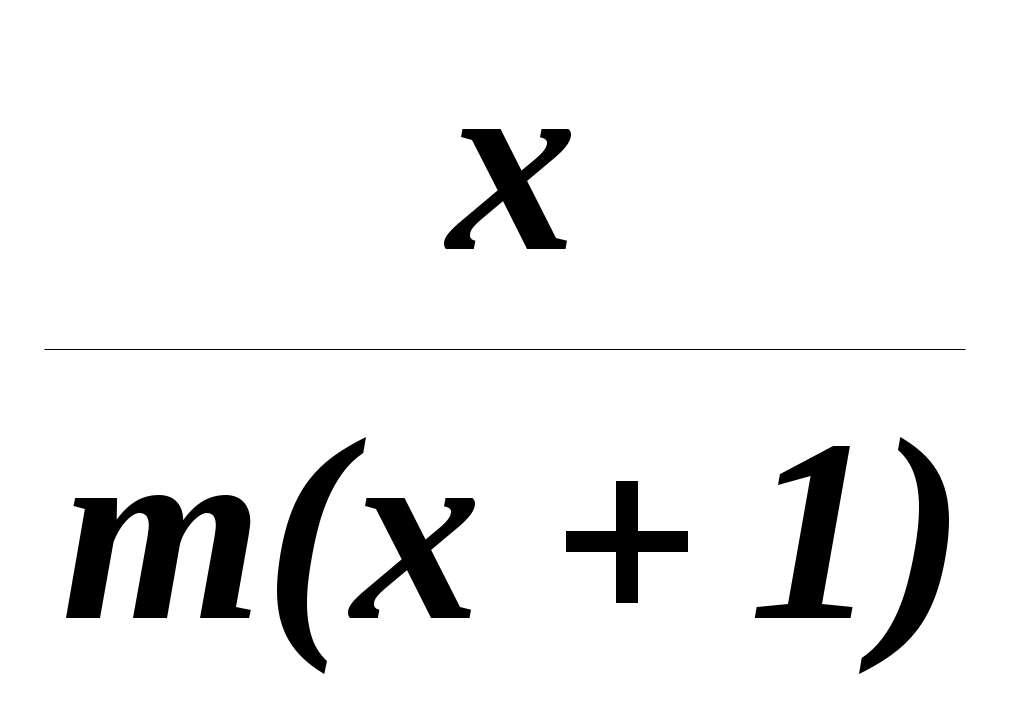
    

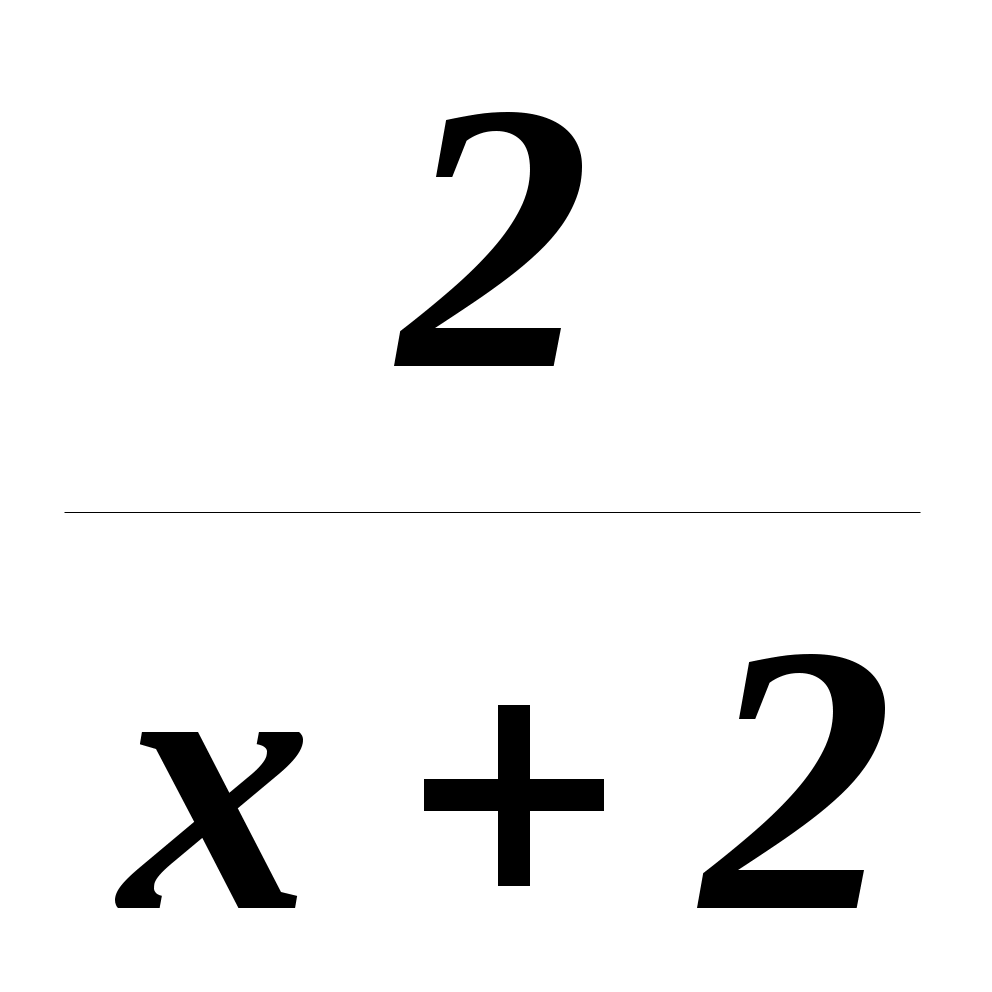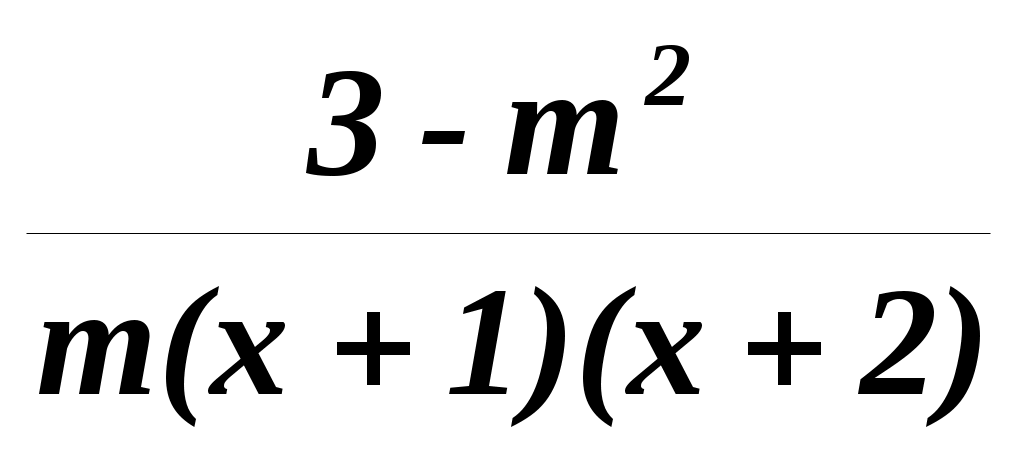Решение:

4. 
   ОДЗ: x 2, x 1,
   

m0.

5. 
   Умножим обе части уравнения на m(x + 1)(x + 2)  0, получим квадратное уравнение (преобразования самостоятельно):
   

x² 2(m  1)x + m² 2m  3 = 0.

6. 
   Найдем D₁.
   

D₁ = (m  1)² (m² 2m  3) = 4.

D₁ 0, значит, уравнение имеет два различных корня при любом m.

x₁ = m  1 2 = m  3; x₂ = m  1+ 2 = m + 1.

7. 
   Найдем значения m, при которых значения x₁, x₂равны 2, 1.
   

а) x₁ = 2, если

---