Файл: Александры Анатольевны.doc

2. Если a – 2 = 0, a = 2, то 0 x = 2 (6 – b),

а) при b 6 0 x = 12 – 2b, корней нет;

б) при b = 6 0 x = 0, x – любое число.

Ответ: при a  0, a  2, b  3a x = ;

при a = 0 корней нет;

при a = 2, b 6 корней нет;

при a = 2, b = 6 x – любое число;

при a 2, b = 3aкорней нет.

Задачу можно усложнить, потребовав исследовать знаки корней, тогда в ответе появится дополнение:

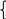
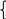
x 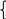 0 при a  0, 0  a  2, a  2,

b  6; b  6; b  6;

x = 0 при b = 6;

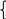
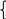
x 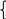 0 при a  0, 0  a  2, a  2,

b 6; b 6; b 6.

Аналогичным требованием можно усложнить задачу 3, тогда:

x 0 при k (4; 6) U(6; 9),

x = 0 при k = 4;

x 0 при k (;  6) U( 6; 4) U(9; ).

Требуется применить метод интервалов.

3. 
    = .
   

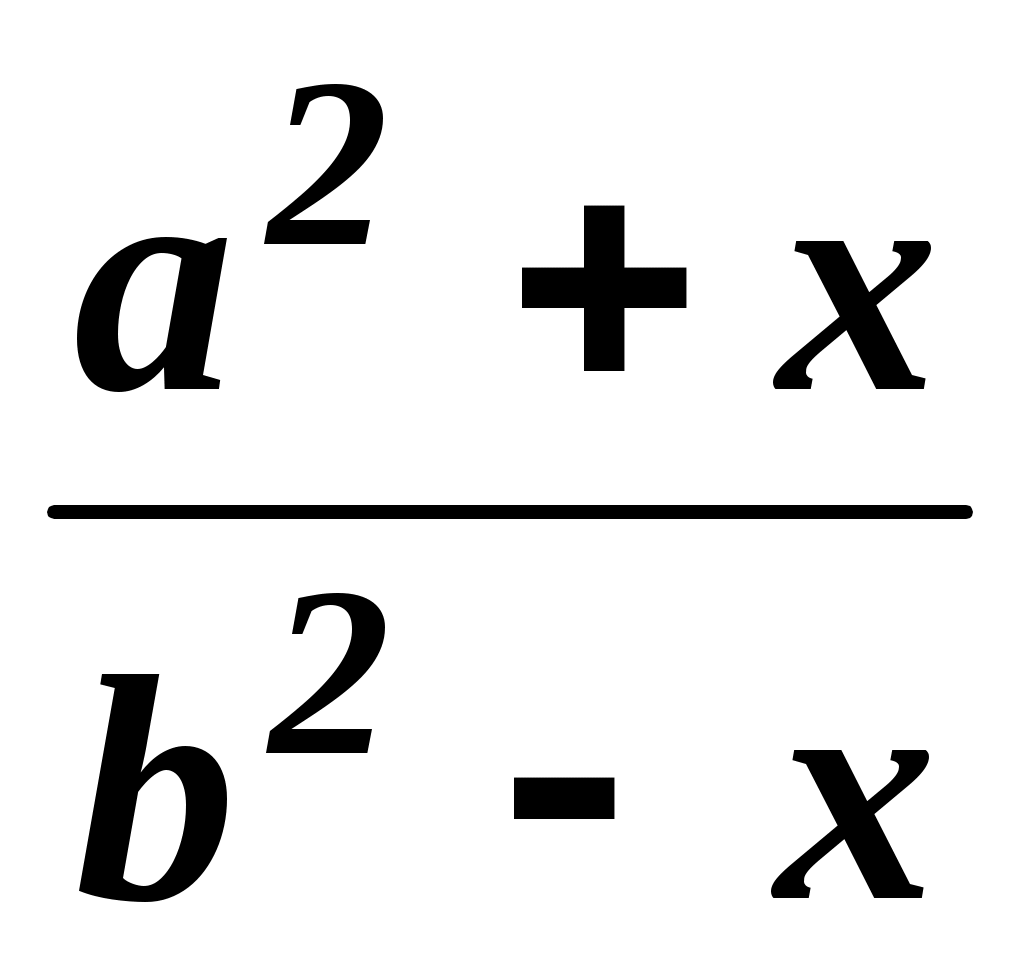
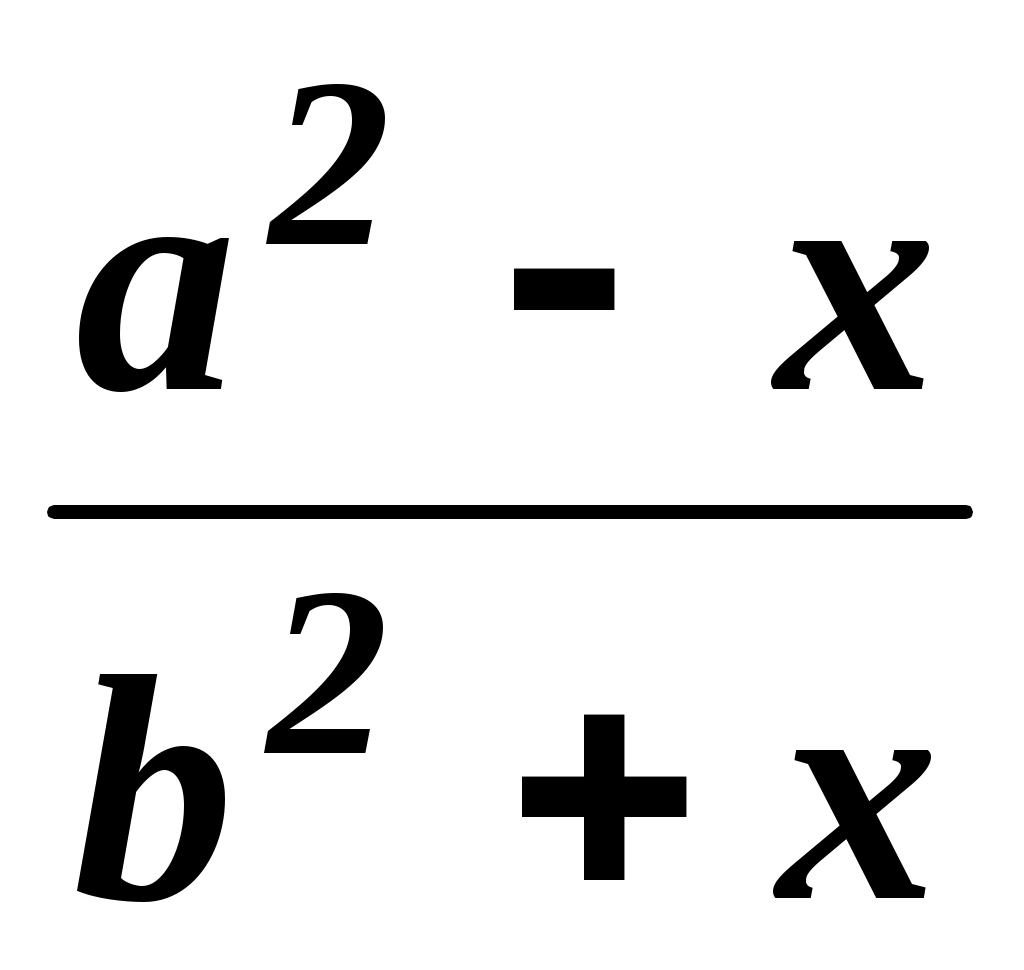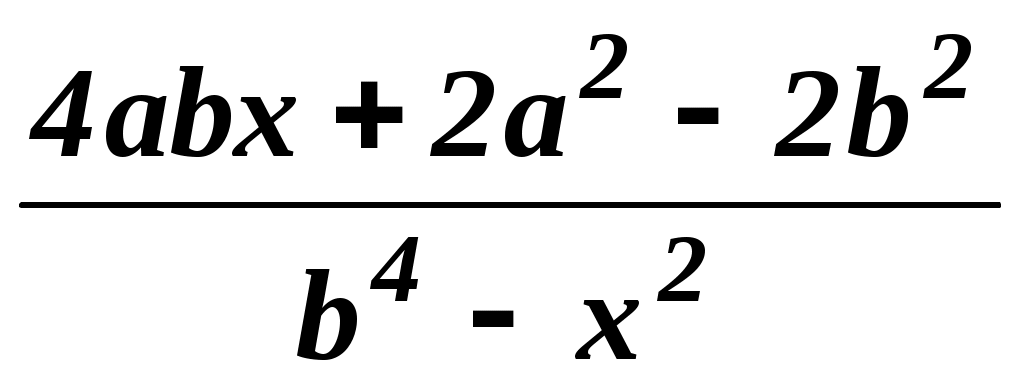Решение:

1. 
   ОДЗ: a  R, b  R, x  b².
   
2. 
   Умножим обе части уравнения на b⁴ – x² 0
   

(a – b)²x = a² – b².

3. 
   Найдем недопустимые значения aи b (ab):
   

1. Если x = b², то (a – b)²b² = a² – b²;

a = ;

2. Если x = –b², то (a – b)²(

---

 b²) = a² – b²,

a = ;

При a = , a = корней нет.

4. 
   (a – b)²x = a² – b².
   

1. Если (a – b)² 0, a  b, то x = ;

x = .

2. Если (a – b)² = 0, a = b, то

0 x = 0, x – любое число, кромеx = b²(из ОДЗ).

Ответ: при a  b, a  , a  x = ;

при a = b, x – любое число, кроме b²;

при a = , a = решений нет.

При решении уравнений такого вида от учащихся требуется строгое соблюдение алгоритма. Если позволять менять местами шаги 3 и 4, то практика показывает, что шаг 3 учащиеся в решении теряют.

Также обращается особое внимание на строгость порядка при выписке ответа, рассмотрение последовательно всех значений параметра согласно решению.

Из ранее изученного восьмиклассникам на факультативе можно предложить такие задания:

3. 
   Решить уравнение x² – 1 + a (x – 1) = 0.
   

Решение: Это уравнение равносильно системе

---

x² – 1 = 0, x² – 1= 0, x = –1, x = –1,

a (x – 1) = 0; a (x – 1) = 0; a (x – 1) = 0; a = 0;

x = 1, x = 1,

a (x – 1) = 0; a – любое число.

Ответ: при a 0, x = 1;

при a = 0, x =  1.

3. 
   Найти все значения параметра bтакие, что при любых значениях параметра a система:
   

x – 2y = a,(1)

ax + 3y = b(2)

имела хотя бы одно решение.

Решение: Систему решаем методом подстановки.

y = ,

ax + 3y = b.

Подставим yв уравнение (2), получим:

ax + = b;

(a + ) x = b + a.

1. 
   Если a +  0, a 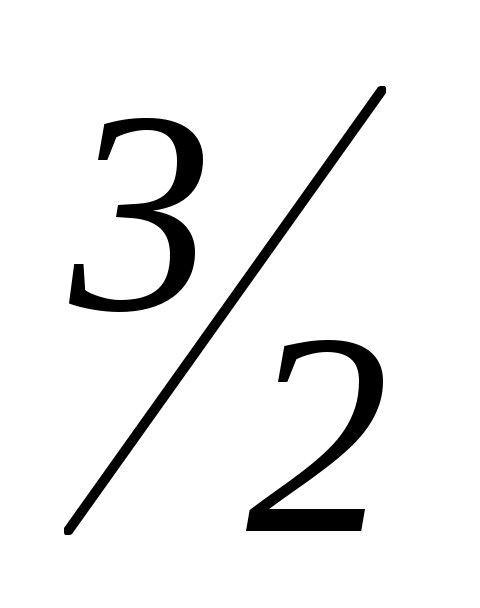 ,то x = .
   

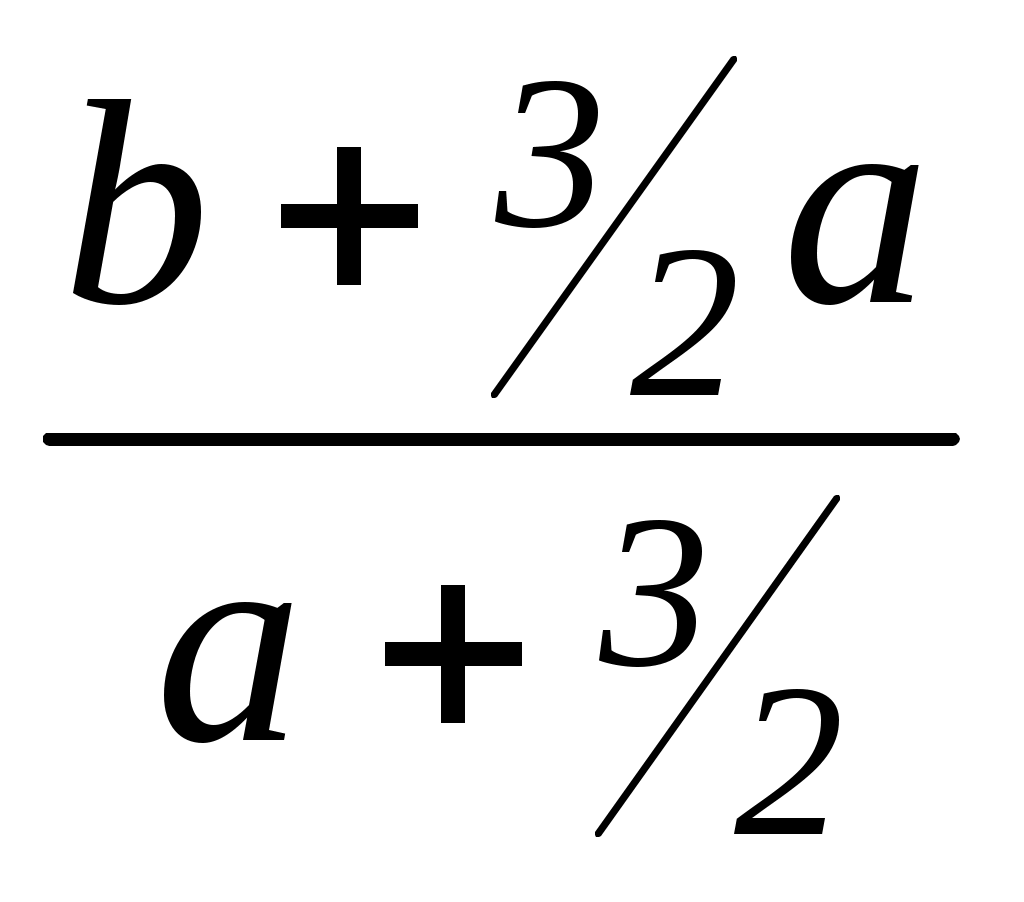Уравнение, а значит, и система, имеют решение при любом действительном b.

2. 
   Если a +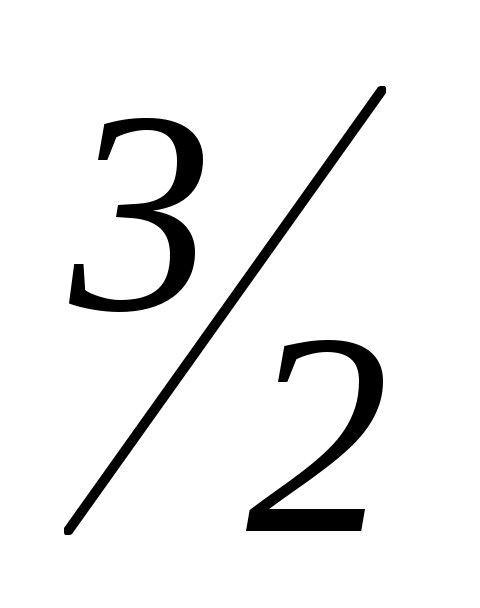 = 0, a = 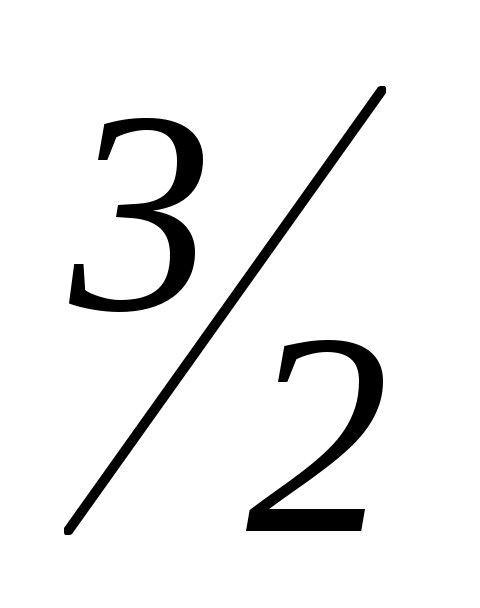 ,то 0 x = b – .
   

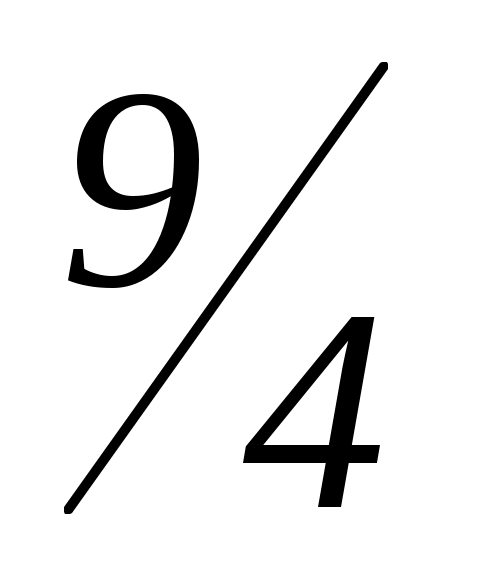Уравнение имеет решение при b = .

Значит, независимо от значения aсистема будет иметь решения при b =

---

.

Ответ:b = .

В восьмом классе более серьезно изучаются графики функции. Восьмиклассники знакомы с элементарными преобразованиями графиков. Поэтому я считаю целесообразным после изучения функции y = рассмотреть задания, в которых применяется графический способ решения, и его применение преимущественно.

12. 
    Сколько корней имеет уравнение x  2 = a при различных значениях параметра a?
    

Решение:

Построим график функции y = x 2, проведя ряд последовательных преобразо-ваний: y = x – 2  y = x 2  y = x 2 , и график функции y = a.

y


y = x 2

y = a (a  2)

2


y = a (a = 2)


y = a (0 a 2)


x


y = a (a = 0)

2

0

2

---

y = a (a  0)


Ответ: при a  0 корней нет;

при a = 0 два корня;

при 0  a  2 четыре корня;

при a = 2 три корня;

при a  0 два корня.

12. 
    Решить уравнение x  1 + x  3 = a.
    

Решение:

Построим графики функций y = x  1 + x  3и y = a.

4 – 2xпри x 1,

y = x  1 + x  3 = 2 при 1 x 3,

2x – 4 при x  3.


y = x  1 + x  3


y


y = a (a  2)

2


y = a (a = 2)


y = a (a  2)


x


1

0

3

1. 
   Если a 2, то ломаная и прямая y = aне пересекаются. Уравнение корней не имеет.
   
2. 
   Если a = 2, то ломаная и прямая совпадают при 1 x 3. Уравнение имеет бесконечно много корней.
   
3. 
   Если a  0, то ломаная и прямая пересекаются в двух точках. Уравнение имеет два корня: 4 – 2x = aили 2 – 4x = a;
   

---