Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 275
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Откуда
.
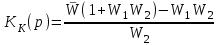Для данной схемы передаточная функция по ошибке имеет вид:
.
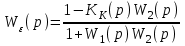Выражение показывает, что если выполнить условие Kk(p) = 1/W2(p), то W(p) = 0. Т.е. ошибка устраняется.
На практике применяют как отдельные виды коррекции, так и их сочетание.
7.2.4. Коррекция времени регулирования
Рассмотрим разомкнутую систему с передаточной функцией, имеющей вид типового инерционного звена:
.
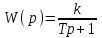Система имеет характеристическое уравнение Тр + 1 = 0, значит, один отрицательный действительный корень р = 1/Т. Решением, при нулевых начальных условиях, будет
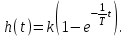
Принимая порог нечувствительности Δ = 0,05 h(∞), для времени регулирования получаем
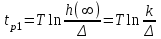. (7.1)
Выполним коррекцию системы с помощью двух корректирующих звеньев по схеме, показанной на рис. 7.4.
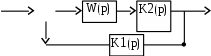
В качестве таковых возьмем усилительные звенья с передаточными функциями K1(р) = k1, K2(р) = k2. Одно из них подключается последовательно к системе, другое включается в линию отрицательной обратной связи.
Запишем передаточную функцию скорректированной системы,
.
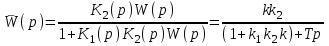Обозначив (1 + k1 k2 k) = A, k k2 = B придем к выводу, что пе-редаточной функции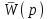
соответствует дифференциальное уравнение
.
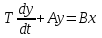Ему отвечает переходная функция
.
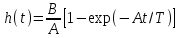( Корень характеристического уравнения действительный: р= – А/Т ).
Время регулирования скорректированной системы:
.
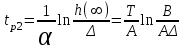
Это время регулирования меньше, чем tр1. Чтобы убедиться, сравним tp2 и tp1 для параметров Т = 1, k = 5, k1 = 2, k2 = 10. h(∞) = B/А. Δ = 0,05 h(∞) = 0, 025. Отношение времен
.
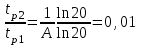В данном случае время регулирования после коррекции сократилось в 100 раз.
7.3. Синтез типовых регуляторов
Типовыми регуляторами называются:
Пропорциональный ( П – регулятор ). Его уравнение
y(t) = kП х(t).
Пропорциально-интегральный ( ПИ – регулятор ). Его уравнение
.
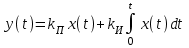Пропорционально - дифференциальный ( ПД – регуля-тор ). Его уравнение
.
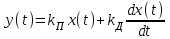Пропорциональный – интегро – дифференциальный ( ПИД – регулятор ). Его уравнение
.
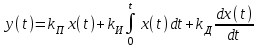Постоянные kП, kИ, kД называют передаточными коэффициентами.
Рассмотрим, каким образом могут быть синтезированы типовые регуляторы с помощью типовых звеньев.
П - регулятор. Структурная схема П - регулятора показана на рис. 7.5.
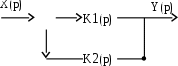
Рис. 7.5. Структурная схема П - регулятора
Звено с передаточной функцией K1(р) охватывается отрицательной обратной связью через звено с передаточной функцией K2(р). Каждое звено – усилительное: K1(р) = k1, K2(р) = k2. Коэффициент усиления звена прямой связи намного больше коэффициента усиления звена обратной связи: k1 >> k2. При таком условии передаточная функция замкнутой системы равна
.
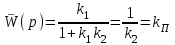То есть передаточный коэффициент П - регулятора определяется коэффициентом усиления звена обратной связи.
П - регулятор обладает малым временем регулирования. Однако, имеет большую статическую ошибку, вследствие чего применяется там, где невелики требования к точности регулирования.
ПИ - регулятор. (Часто называют «изодромный регулятор»). Структурно может быть реализован двумя схемами.
Схема 1. Соединяют параллельно усилительное и интегрирующие звенья, рис. 7.6.
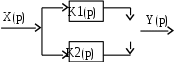
Рис. 7.6. Структурная схема ПИ - регулятора
Передаточная функция ПИ - регулятора получается сложением передаточных функций звеньев:
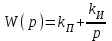
Передаточная функция ПИ - регулятора имеет два параметра настройки: передаточный коэффициент kП и передаточный коэффициент kИ = 1/ТИ, где ТИ – время интегрирования.
Схема 2. Усилительное звено с передаточной функцией K1(р) = k1 охватывается отрицательной обратной связью через инерционное звено с передаточной функцией K2(р) = k2/(Т2 р+1) и к ним последовательно присоединяется интегрирующее звено с передаточной функцией K3(р) = k3/р, рис. 7.7.
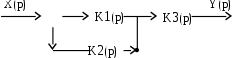
Рис. 7.7. Структурная схема ПИ - регулятора
Найдем передаточную функцию регулятора при условии k1 >> 1.
.
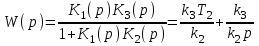Полагая k3T2/k2 = kП, k3/k2 = kИ, получаем:
.
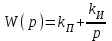Вид передаточной функции тот же, что и полученный ранее, но настроечные параметры сами зависят от коэффициентов k2, k3, T2. (Зависимость от коэффициента k1 отсутствует).
При очень малом передаточном коэффициенте kИ регулятор работает как усилительное звено. При очень малом передаточном коэффициенте kП регулятор становится интегрирующим звеном. Пропорциональная составляющая обеспечивает быстродействие, интегральная – точность.
ПД - регулятор. Структурную схему можно было бы получить, соединив параллельно усилительное и идеальное дифференцирующее звено, рис. 7.8.
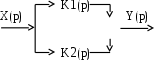
Рис. 7.8. Структурная схема ПД - регулятора
Передаточная функция ПД - регулятора, отвечающая схеме на рис. 7.8.
,
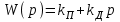где передаточный коэффициент kД = Т, постоянной времени дифференцирующего звена.
Однако, идеальное дифференцирующее звено не реализуется. Поэтому составляют эквивалентную схему, охватив отрицательной обратной связью через инерционное звено усилительное звено с большим коэффициентом усиления
, рис. 7.9.
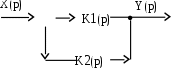
Рис. 7.9. Структурная схема ПД - регулятора
На схеме K1(р) = k1, K2(р) = k2/(Т2р + 1).
Передаточная функция регулятора, при условии k1 >> 1,
.
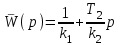Вводя новые обозначения kП = 1/k2, kД = T2/k2, находим:
.
То есть схема, не содержащая дифференцирующего звена, работает как ПД - регулятор.
С уменьшением передаточного коэффициента kП регулятор начинает работать как дифференцирующее звено, с уменьшением передаточного коэффициента kД приобретает свойства усилительного звена.
Наличие дифференцирующей составляющей увеличивает быстродействие, снижает динамическую ошибку.
ПИД - регулятор. Синтез можно осуществить несколькими способами. На схеме рис. 7.10 показан один из них.
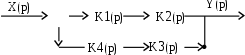
Рис. 7.10. Структурная схема ПИД - регулятора
Звенья с передаточными функциями K1(p) = k1 и K2(p) = 1/Т2р, соединенные последовательно, охватываются отрицательной обратной связью через звенья K3(р) = k3p/(T3p + 1) и K4(р) = 1/(Т4 р + 1), соединенные тоже последовательно. Передаточная функция получается в виде:
.
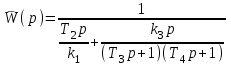Если потребовать k1 >> 1, то первым слагаемым в знаменателе можно пренебречь. Полагая (Т3 + Т4)/k3 = kП, Т3Т4/k3 = kД, 1/k3 = kИ , получаем:
.
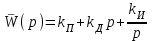Структурная схема на рис. 7.10. работает как ПИД - регулятор.
ПИД - регулятор является более универсальным, чем остальные регуляторы. Он позволяет осуществить различные законы регулирования благодаря трем параметрам настройки. Так, при kД, kИ = 0 получается П - регулятор. При kД = 0 получаем ПИ - регулятор. При kИ = 0 получается ПД - регулятор.
1. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. – СПб, «Профессия», 2004. – 752 с.
2. Наладка средств автоматизации и автоматических систем регулирования: Справочное пособие / А.С. Клюев и др. – М.: Энергоатомиздат, 1989. – 368 с.
3. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). – М.: Машиностроение, 1977. – 464 с.
4. Дорф Р., Бишоп Р. Современные системы управления. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.
ПРИЛОЖЕНИЕ
Таблица преобразования Лапласа для некоторых функций
Откуда
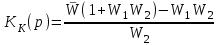.Для данной схемы передаточная функция по ошибке имеет вид:
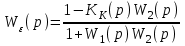.Выражение показывает, что если выполнить условие Kk(p) = 1/W2(p), то W(p) = 0. Т.е. ошибка устраняется.
На практике применяют как отдельные виды коррекции, так и их сочетание.
7.2.4. Коррекция времени регулирования
Рассмотрим разомкнутую систему с передаточной функцией, имеющей вид типового инерционного звена:
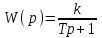.Система имеет характеристическое уравнение Тр + 1 = 0, значит, один отрицательный действительный корень р = 1/Т. Решением, при нулевых начальных условиях, будет
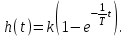
Принимая порог нечувствительности Δ = 0,05 h(∞), для времени регулирования получаем
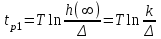. (7.1)Выполним коррекцию системы с помощью двух корректирующих звеньев по схеме, показанной на рис. 7.4.
Рис. 7.4. Корреляция времени регулирования двумя
корректирующими звеньями
В качестве таковых возьмем усилительные звенья с передаточными функциями K1(р) = k1, K2(р) = k2. Одно из них подключается последовательно к системе, другое включается в линию отрицательной обратной связи.
Запишем передаточную функцию скорректированной системы,
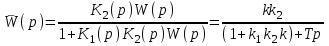.Обозначив (1 + k1 k2 k) = A, k k2 = B придем к выводу, что пе-редаточной функции
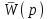соответствует дифференциальное уравнение 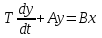.Ему отвечает переходная функция
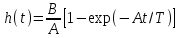.( Корень характеристического уравнения действительный: р= – А/Т ).
Время регулирования скорректированной системы:
.
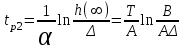
Это время регулирования меньше, чем tр1. Чтобы убедиться, сравним tp2 и tp1 для параметров Т = 1, k = 5, k1 = 2, k2 = 10. h(∞) = B/А. Δ = 0,05 h(∞) = 0, 025. Отношение времен
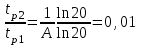.В данном случае время регулирования после коррекции сократилось в 100 раз.
7.3. Синтез типовых регуляторов
Типовыми регуляторами называются:
Пропорциональный ( П – регулятор ). Его уравнение
y(t) = kП х(t).
Пропорциально-интегральный ( ПИ – регулятор ). Его уравнение
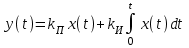. Пропорционально - дифференциальный ( ПД – регуля-тор ). Его уравнение
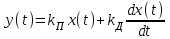. Пропорциональный – интегро – дифференциальный ( ПИД – регулятор ). Его уравнение
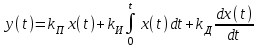.Постоянные kП, kИ, kД называют передаточными коэффициентами.
Рассмотрим, каким образом могут быть синтезированы типовые регуляторы с помощью типовых звеньев.
П - регулятор. Структурная схема П - регулятора показана на рис. 7.5.
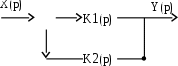
Рис. 7.5. Структурная схема П - регулятора
Звено с передаточной функцией K1(р) охватывается отрицательной обратной связью через звено с передаточной функцией K2(р). Каждое звено – усилительное: K1(р) = k1, K2(р) = k2. Коэффициент усиления звена прямой связи намного больше коэффициента усиления звена обратной связи: k1 >> k2. При таком условии передаточная функция замкнутой системы равна
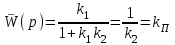.То есть передаточный коэффициент П - регулятора определяется коэффициентом усиления звена обратной связи.
П - регулятор обладает малым временем регулирования. Однако, имеет большую статическую ошибку, вследствие чего применяется там, где невелики требования к точности регулирования.
ПИ - регулятор. (Часто называют «изодромный регулятор»). Структурно может быть реализован двумя схемами.
Схема 1. Соединяют параллельно усилительное и интегрирующие звенья, рис. 7.6.
Рис. 7.6. Структурная схема ПИ - регулятора
Передаточная функция ПИ - регулятора получается сложением передаточных функций звеньев:
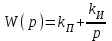
Передаточная функция ПИ - регулятора имеет два параметра настройки: передаточный коэффициент kП и передаточный коэффициент kИ = 1/ТИ, где ТИ – время интегрирования.
Схема 2. Усилительное звено с передаточной функцией K1(р) = k1 охватывается отрицательной обратной связью через инерционное звено с передаточной функцией K2(р) = k2/(Т2 р+1) и к ним последовательно присоединяется интегрирующее звено с передаточной функцией K3(р) = k3/р, рис. 7.7.
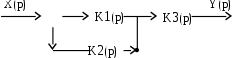
Рис. 7.7. Структурная схема ПИ - регулятора
Найдем передаточную функцию регулятора при условии k1 >> 1.
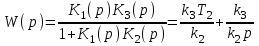.Полагая k3T2/k2 = kП, k3/k2 = kИ, получаем:
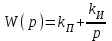.Вид передаточной функции тот же, что и полученный ранее, но настроечные параметры сами зависят от коэффициентов k2, k3, T2. (Зависимость от коэффициента k1 отсутствует).
При очень малом передаточном коэффициенте kИ регулятор работает как усилительное звено. При очень малом передаточном коэффициенте kП регулятор становится интегрирующим звеном. Пропорциональная составляющая обеспечивает быстродействие, интегральная – точность.
ПД - регулятор. Структурную схему можно было бы получить, соединив параллельно усилительное и идеальное дифференцирующее звено, рис. 7.8.
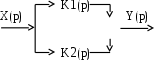
Рис. 7.8. Структурная схема ПД - регулятора
Передаточная функция ПД - регулятора, отвечающая схеме на рис. 7.8.
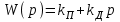,где передаточный коэффициент kД = Т, постоянной времени дифференцирующего звена.
Однако, идеальное дифференцирующее звено не реализуется. Поэтому составляют эквивалентную схему, охватив отрицательной обратной связью через инерционное звено усилительное звено с большим коэффициентом усиления
, рис. 7.9.
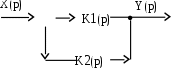
Рис. 7.9. Структурная схема ПД - регулятора
На схеме K1(р) = k1, K2(р) = k2/(Т2р + 1).
Передаточная функция регулятора, при условии k1 >> 1,
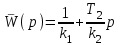.Вводя новые обозначения kП = 1/k2, kД = T2/k2, находим:
.То есть схема, не содержащая дифференцирующего звена, работает как ПД - регулятор.
С уменьшением передаточного коэффициента kП регулятор начинает работать как дифференцирующее звено, с уменьшением передаточного коэффициента kД приобретает свойства усилительного звена.
Наличие дифференцирующей составляющей увеличивает быстродействие, снижает динамическую ошибку.
ПИД - регулятор. Синтез можно осуществить несколькими способами. На схеме рис. 7.10 показан один из них.
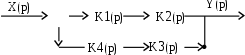
Рис. 7.10. Структурная схема ПИД - регулятора
Звенья с передаточными функциями K1(p) = k1 и K2(p) = 1/Т2р, соединенные последовательно, охватываются отрицательной обратной связью через звенья K3(р) = k3p/(T3p + 1) и K4(р) = 1/(Т4 р + 1), соединенные тоже последовательно. Передаточная функция получается в виде:
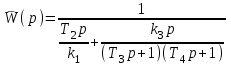.Если потребовать k1 >> 1, то первым слагаемым в знаменателе можно пренебречь. Полагая (Т3 + Т4)/k3 = kП, Т3Т4/k3 = kД, 1/k3 = kИ , получаем:
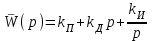.Структурная схема на рис. 7.10. работает как ПИД - регулятор.
ПИД - регулятор является более универсальным, чем остальные регуляторы. Он позволяет осуществить различные законы регулирования благодаря трем параметрам настройки. Так, при kД, kИ = 0 получается П - регулятор. При kД = 0 получаем ПИ - регулятор. При kИ = 0 получается ПД - регулятор.
Литература
1. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. – СПб, «Профессия», 2004. – 752 с.
2. Наладка средств автоматизации и автоматических систем регулирования: Справочное пособие / А.С. Клюев и др. – М.: Энергоатомиздат, 1989. – 368 с.
3. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). – М.: Машиностроение, 1977. – 464 с.
4. Дорф Р., Бишоп Р. Современные системы управления. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.
ПРИЛОЖЕНИЕ
Таблица преобразования Лапласа для некоторых функций
| № | Оригинал | Изображение |
| 1 |  |  |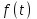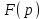
| 2 |  |  |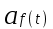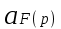
| 3 |  |  |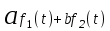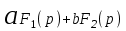
| 4 |  |  |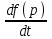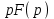
| 5 |  |  |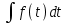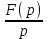
| 6 |  |  |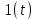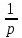
| 7 |  |  |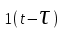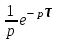
| 8 |  |   |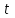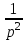
| 9 |  |  |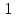
| 10 |  |  |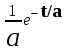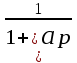
| 11 |  |  |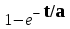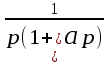
| 12 |  |  |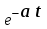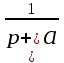
| 13 |  |  |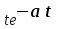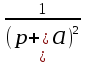
| 14 |  |  |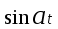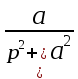
| 15 |  |  |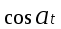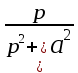
| 16 |  |  |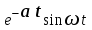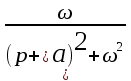
| 17 | 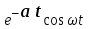 | 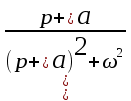 |