Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx

Из уравнения:



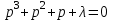
выделим: 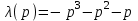. Полагая , находим: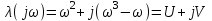

,

,



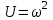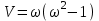
Полагая V(ω) = 0, найдем частоты и точки пересечения кривой с осью абсцисс: ω₁ = 0, U(0) = 0, ω₂ = 1, U(1) = 1. Неограниченно увеличивая ω выясним, что U  ∞ и V  ∞, кривая уходит в бесконечность в верхней правой полуплоскости. В интервале 0  ω  1 U  1 и V  0. Для промежуточных значений U и Vход кривой уточняется заданием соответствующих частот. По совокупности данных строится кривая D-разбиения для положительных частот и дополняется зеркальным отображением. Наносится штриховка слева при движении по кривой от – ∞ к + ∞.

Результат показан на рис. 5.23. Интервал устойчивых значений λ есть отрезок действительной оси от 0 до 1.

Контрольная проверка по критерию Гурвица для λ = 0,5.

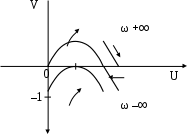
Рис. 5.23. Кривые D- разбиения по условиям примера 5.13
Записываем характеристическое уравнение:

.

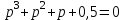Коэффициенты: a₀ = 1, a₁ = 1, a₂ = 1, a₃ = 0,5. Действительно, a₁a₂ – a₀a₃ > 0, система устойчива.
П

ример 5.14.

Дано характеристическое уравнение вида:

.

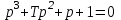Требуется найти значения Т, при которых система будет устойчивой.
Назначив Т параметром, выделим λ:



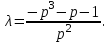
Полагая 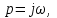получаем: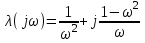



Запишем действительную и мнимую части:



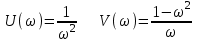
Анализ формул показывает:

- при ω = 0 U = ∞, V = ∞;

- при ω = 1 U = 1, V = 0; кривая V (U) пересекает действительную ось;

- при ω = ∞ U

---

= 0, V = – ∞;

Кривая начинается в + ∞, пересекает ось абсцисс и неограниченно приближается к мнимой оси, уходя в  ∞.

Для уточнения хода кривой V (U) можно взять точки:

ω = 0,5, U = 4, V = 1,5.

ω = 2, U = 0,25, V = – 1,5;

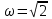, U = 0,5 V = – 0,7;

ω = 0,82, U = 1,5, V = – 0,4.

Построив на плоскости (U, V) кривую для положительных частот, отображаем ее зеркально относительно действительной оси и получаем кривую для отрицательных частот, рис. 5.24. Нанеся штриховку, получаем область устойчивости. Устойчивость системы обеспечивают те значения параметра λ, которые располагаются на отрезке действительной оси от 1 до ∞. Контрольная проверка по критерию Гурвица подтверждает вывод.

Рис. 5.24. Кривые D- разбиения по условиям примера 5.14
П

ример 5.15.

Дано характеристическое уравнение вида

.

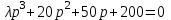Требуется найти интервал значений параметра λ, при которых САР будет устойчивой.
Записав



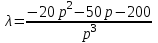
и положив p = jω, получаем комплексный параметр λ в виде

.

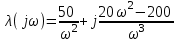Выделяем действительную и мнимую части:

.
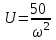
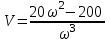Задаем ω и рассчитываем U и V для построения кривой V(U):

ω	U	V
0	∞	– ∞
2,36	9	– 6,7
3,16	5	0
4	3,1	1,9
5	2	2,4
5,45	1,68	2,44
6	1,4	2,4
10	0,5	1,8
∞	0	0

---

Построив кривую для положительных ω, дополняем ее зеркально отображенной (для отрицательных ω). Результат показан на рис. 5.25.

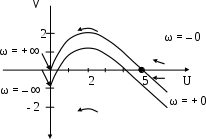
Рис. 5.25. Кривые D- разбиения по условиям примера 5.15

Вывод: САР устойчива при значениях λ, принадлежащих интервалу 0  λ  5. Границе устойчивости отвечают λ = 0 и λ = 5.

Контрольная проверка по критерию Гурвица: все коэффициенты характеристического уравнения больше нуля, определитель a₁a₂ - a₀a₃ > 0.

5.5.2. D - разбиение по двум параметрам
В основе лежит допущение, что в характеристическом уравнении можно выделить два параметра, М и N, которые могут изменяться, а остальные параметры заданы. Параметром может быть коэффициент или комбинация коэффициентов.

Если параметры М и N входят в характеристическое уравнение линейно, то характеристическое уравнение может быть представлено в виде

MQ(p) + NR(p) + H(p)=0, (5.7)

где Q, R, H – некоторые полиномы.

Выделение областей устойчивости в плоскости параметров N и М достигается следующей процедурой.
Подставляем в характеристическое уравнение p = jω. Полиномы Q, R, H распадаются на вещественные и мнимые части:

---

,

,

.

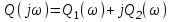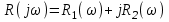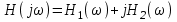Теперь их надо ввести в характеристическое уравнение (5.7) и выделить действительные и мнимые слагаемые:


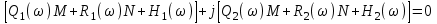
Если комплексное выражение равно нулю, значит его действительное и мнимое слагаемые по отдельности равны нулю:

,

.

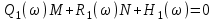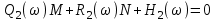Получается два линейных уравнения для определения параметров M и N:

,

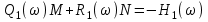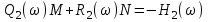. (5.8)

Величины Q₁, Q₂, R₁, R₂ рассматриваются как коэффициенты, а М и N – как переменные.

Определитель системы

.

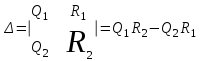Определители параметра М и параметра N:

.

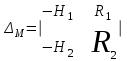
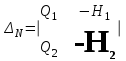Определитель 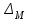получается из определителя системы заменой элементов первого столбца свободными членами системы. Определитель 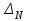– заменой элементов второго столбца свободными членами системы.

Для конкретного значения ω:

.

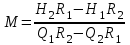
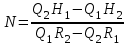На плоскости M, N это будет точка. Задавая ωот нуля до бесконечности, в плоскости M, N можно построить кривую, которая и есть граница D - разбиения. Система уравнений (5.8) имеет решение, если Δ ≠ 0 и Δ_M  0, Δ_N ≠ 0; и не имеет решения, если Δ = 0 (точка с координатами (M, N) уходит в бесконечность). В случае Δ = 0, Δ_M

---

= 0, Δ_N = 0, значения M и N становятся неопределенными. Уравнения (5.8) становятся зависимыми и определяют собой не точку, а прямую в плоскости M, N. Такая прямая называется особой прямой. В большинстве случаев особые прямые получаются для ω = 0 и ω = ∞.

Область устойчивости выделяется штриховкой. Правило штриховки следующее.

Если определитель Δ > 0, то двигаясь по D - кривой от ω = – ∞ до ω = + ∞, штрихуют левую сторону. Если Δ < 0, то штрихуют правую сторону ( знак определителя меняется, если +ω заменить на – ω ).






Пример 5.16.

Дано характеристическое уравнение

.

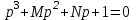Произвести D - разбиение в плоскости параметров M и N.
Полагая p= jω, находим: .

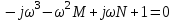Запишем для условий задачи систему уравнений (5.8). Если какой-то из полиномов Q₁, Q₂, R₁, R₂ окажется равным нулю, вместо него надо поставить ноль.

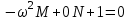; надо записать ,

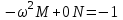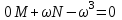; надо записать .

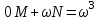Определитель системы будет: .

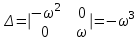Определители параметров:

,

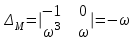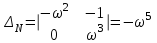
Получаем: 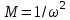, 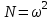. Функциональная зависимость между коэффициентами M и N представляет собой равнобочную гиперболу: MN = 1. График представлен на рис. 5.26.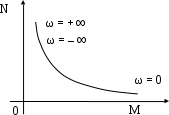

Рис. 5.26. Кривые D- разбиения по условиям примера 5.16
Верхняя ветвь гиперболы уходит в ∞ как для положительных, так и для отрицательных значений ω. Нижняя ветвь гиперболы уходит в ∞ при стремлении к нулю положительных и отрицательных значений ω. Учитывая эти обстоятельства

---