Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx

.

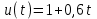
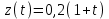Найти ошибку системы.
Передаточные функции ошибок получают вид





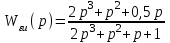
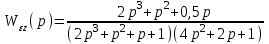
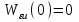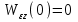
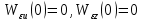, , так что

,

.

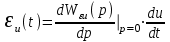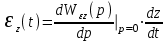После вычисления получаем:

, .

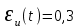
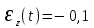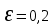6.2. Косвенные показатели качества
Корневые показатели

Рассмотрим, как влияет на переходной процесс расположение корней характеристического уравнения на комплексной плоскости. В качестве примера рассмотрим систему, описываемую дифференциальным уравнением третьего порядка.

Характеристическое уравнение имеет три корня и соответствующее решение имеет три слагаемых:

.

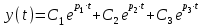Пусть все корни имеют отрицательную действительную часть.

Для действительных корней (р₁ = – σ₁, р₂ = – σ₂, р₃ = – σ₃) кривая у(t) переходного процессамонотонная, рис. 6.3.

Если два корня комплексных и один действительный (р_1,2 = – σ₁ ± jω₁ , р₃ = – σ₃), причем действительный расположен ближе к мнимой оси, а комплексные дальше, то кривая переходного процессаприобретает слабо выраженную колебательность, рис. 6.4.

Если комплексные корни р_1,2 = – σ₁ ± jω₁ располагаются вблизи мнимой оси, а действительный р₃ = – σ₃ на отдалении, переходной процесс приобретает ярко выраженный колебательный характер, рис.6.5. Чем ближе комплексные корни к мнимой оси, тем медленнее затухают колебания, тем длительнее переходной процесс (больше время

---

t_p). Чисто мнимые корни дают незатухающие гармонические колебания.

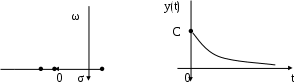
Рис. 6.3. Монотонная кривая переходного процесса


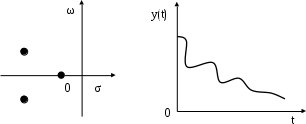
6.4. Апериодический процесс с колебательной составляющей

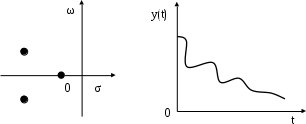
Рис. 6.5. Затухающий колебательный процесс

По рисункам можно заключить, что точность, время регулирования, перерегулирование и число колебаний зависят от распределения корней характеристического уравнения на комплексной плоскости. Очевидно, количественные соотношения, характеризующие расположение корней, так же будут являться показателями качества регулирования.

Получим связанные с распределением корней показатели качества.

Чем ближе корни к мнимой оси, тем медленнее затухают колебания и увеличивается время регулирования t_p. Значит, ближайший к мнимой оси корень будет влиять больше, чем остальные. Обозначим величину ближайшего к мнимой оси корня через α. На рис. 6.6 это отрезок отрицательной оси абсцисс. И построим переходную функцию (рис. 6.7) по уравнению

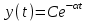
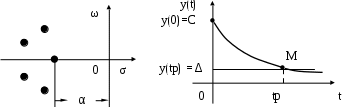
Рис. 6.6. Параметр α – запас устойчивости

Рис. 6.7. Переходная функция, связь tp и Δ

В начальный момент y(0) = C. В момент времени t_p кривая пересечет порог нечувствительности. В точке М, где кривая пересекается с прямой y = Δ

.

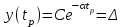За время регулирования величина y(t_p) станет меньше в m раз по сравнению с величиной в начальный момент. То есть,

.

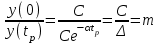Откуда

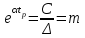, или .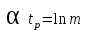

Величина действительной части корня, обеспечивающего заданное время регулирования, должна быть:

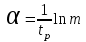. (6.6)

Формула (6.6.) дает приближенную оценку α, потому что остались без внимания другие слагаемые полного решения уравнения.

---

Параметр α представляет собой показатель качества, который называют «запас устойчивости» или «степень устойчивости». Это абсолютное значение действительной части ближайшего к мнимой оси корня. Чем меньше α, тем ближе система к границе устойчивости, тем больше время регулирования. При α = 0 (система на границе устойчивости) время регулирования становится бесконечно большим.

Рассмотрим еще один показатель качества, связанный с распределением корней: угол θ между отрицательной полуосью абсцисс и прямой, проведенной из начала координат к корню с максимальной мнимой частью, рис. 6.8. В этот угол вписывается половина всех наиболее удаленных от мнимой оси корней. Корень с максимальной мнимой частью дает наибольший вклад в колебания. Величину

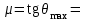
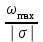(6.7)

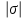
называют колебательностью системы. Чем меньше угол θ, тем меньше колебательность. В формуле (6.7) 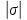есть абсолютная величина действительной части комплексного корня .

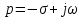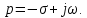
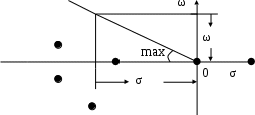
Рис. 6.8. Параметр колебательности системы
П

ример 6.3.

Найти время регулирования и число колебаний за время регулирования для трех характеристических уравнений:

,

,

.

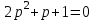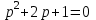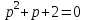Требуется, чтобы управляемая величина уменьшилась за время регулирования в е раз (е = 2,718).
1. Корни уравнения 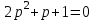будут:

, ,

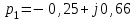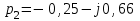т.е.

---

, , , .

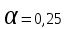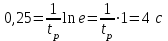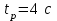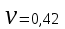2. Корни уравнения будут: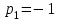

, ,

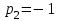т.е. , , .

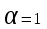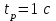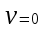3. Корни уравнения будут: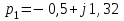

, ,

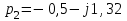т.е. , , .
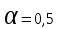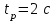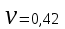П

ример 6.4.

Для переходной функции инерционного звена:



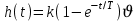
найти, через какое время t_ величина h(t) будет отличаться от своего предельного значения на ε единиц?
Предельное значение h равно k единицам (при t= ∞)

Решение должно подчиняться условию h = k - ε при t=t_ Введем его в переходную функцию



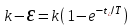
и получим: ε = kexp(– t_/T). Посредством логарифмирования находим:

.

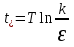П

ример 6.5.

Передаточная функция системы

.

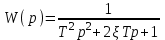Найти запас устойчивости и колебательность.
Характеристическое уравнение 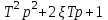имеет корни

.

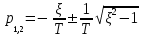Колебания будут, если

---

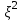< 1.

Сопоставим с общей формулой записи корня: р = σ + jω.

Выясняется:

, .

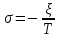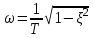Запас устойчивости .

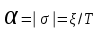Колебательность .

---
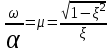