Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx

Комплексная частотная характеристика

.

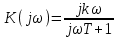Действительная и мнимая частотные характеристики

, .

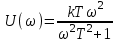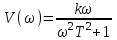Амплитудная частотная характеристика

.

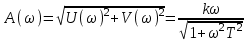У идеального дифференцирующего звена с увеличением ω амплитуда линейно возрастает до ∞. У реального дифференцирующего звена амплитуда возрастает монотонно, стремясь к пределу k/T.

Фазовая частотная характеристика

φ(ω) = arctg .

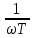При ω = 0, φ = 90, как у идеального дифференцирующего звена. Но мере увеличения частоты опережение по фазе уменьшается до нуля.

Логарифмическая амплитудная частотная характеристика

.

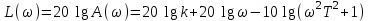Найдем асимптотические прямые логарифмической амплитудной частотной характеристики. В области ω < 1 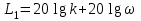. В области ω > 1 L₂ = 20 lg (k/T).

Прямая L₁ пересекает ординату в точке с координатами lg ω= 0, L₁ = 20 lg k, абсциссу – в точке с координатами lg ω = lg(1/k), L₁ = 0. Cледует учесть, что k  1 и потому lg (1/k) – число отрицательное. Прямая L₂ параллельна оси абсцисс, пересекает ординату в точке lg ω= 0, L₂ = 20 lg(k/T). Прямые L₁ и L₂ пересекаются в точке с абсциссой lg ω= lg (1/T). График представлен на рис. 3.6.

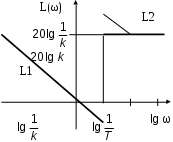
Рис. 3.6. Асимптоты ЛАЧХ реального дифференцирующего звена
Чтобы найти переходную функцию, в операторном уравнении заменим X(p) на 1/p:

.

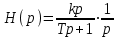Таблица преобразований Лапласа указывает, что

---

.

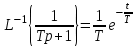
Значит, переходная функция имеет вид

.

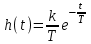В момент t = 0 h(0) = k/T. По мере увеличения t, функция h(t) экспоненциально уменьшается до нуля. Напомним: в идеальном дифференцирующем звене переходная функция имеет вид импульса.

3.6. Колебательное звено
Математической моделью колебательного звена является линейное дифференциальное уравнение второго порядка с постоянными коэффициентами

, (3.7)

при условии .

Колебательные процессы характеризуются двумя важными параметрами: коэффициентом затухания ξ и резонансной частотой ω₀. Они выражаются через постоянные времени уравнения (3.7): ξ = Т₀/2Т, ω₀ = 1/Т. Если ввести ξ в уравнение (3.7), оно получает вид, более удобный для исследования колебательного процесса:

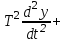2 ξ Т 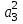+ y = kx. (3.8)

Дифференциальному уравнению (3.8) соответствует операторное уравнение

(T²p² + 2 ξ Tp + 1) Y(p) = kX(p),

из которого получается передаточная функция

.

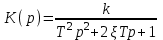Если выходная величина не изменяется (dy/dt = 0, p = 0) передаточная функция вырождается в коэффициент усиления: K(0) = k.

Комплексная частотная характеристика звена

.

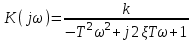Действительная и мнимая частотные характеристики имеют вид:

,

.

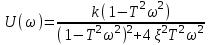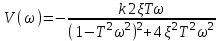Амплитудная частотная характеристика колебательного звена

.

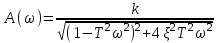У колебательного звена кривая A(ω) имеет пик, вершина которого отвечает частоте ω₀ = 1/T (рис. 3.7). То есть резонансной частоте. Максимальная величина амплитуды равна k/ 2ξ. Пик выше, если больше коэффициент усиления и меньше коэффициент затухания.

Фазовая частотная характеристика в интервале изменения частоты от ω = 0 до ω = 1/T рассчитывается по формуле

---

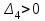
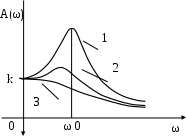
Рис. 3.7. Зависимость амплитуды от частоты.

1 – ξ = 0,20, 2 – ξ = 0,5, 3 – ξ = 0,75

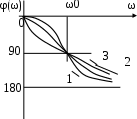
Рис. 3.8. Фазовая частотная характеристика колебательного звена.

1 – ξ = 0,2, 2 – ξ = 0,4, 3 – ξ= 0,8

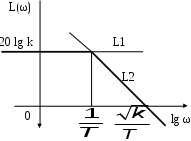
Рис. 3.9. Асимптотическая ЛАЧХ в интервале 0,3 < ξ < 1

При ω = 0 φ(ω) = 0. Значению ω₀ = 1/T соответствует запаздывание – 90 . С увеличением ω запаздывание увеличивается и расчет надо вести по формуле

.

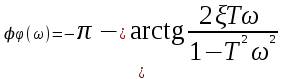Характер кривых показан на рис. 3.8.

Логарифмическая амплитудная частотная характеристика имеет вид:

L(ω) = 20 lg k– 10 lg (1-T²ω²)² + 4 ξ²T²ω².

Форма этой кривой зависит от коэффициента затухания ξ. В интервале 0,3  ξ  1 приемлемо асимптотическое представление. В области ω  1 L₁ = 20 lgk. В области ω  1 L₂ = 20 lg (k/T²) – 40 lg ω. Условие сопряжения прямых ω₀ = 1/T, т.е. на резонансной частоте. Пересечение прямой L₂ c осью абсцисс при ω = 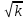/T. Расположение асимптотических прямых показано на рис. 3.9.

В случае ξ  0,3 нужно пользоваться точной ЛАЧХ из-за возрастания амплитуды в окрестности резонансной частоты.

Переходная функция есть решение уравнения (3.8) при x= 1:

,

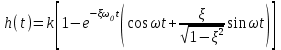где ω₀ = 1/T, .

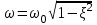Переходная функция описывает затухающие колебания. Колебания затухают тем медленнее, чем меньше ξ. При ξ = 0 колебания совершаются с постоянной амплитудой, т.е. становятся гармоническими. Звено, реализующее гармонические колебания называют консервативным.

3.7. Апериодическое звено

второго порядка
Оно описывается тем же дифференциальным уравнением (3.7.), что и колебательное звено, но при условии Т₀ > 2T. Корни характеристического уравнения становятся действительными, звено перестает быть колебательным и превращается в апериодическое.

Операторное уравнение

(T²p² + T₀ p +1)Y(p) = kX(p).

Передаточная функция

---

.

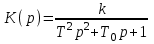
При отсутствии изменения выходной величины (p = 0) K(p) = k, коэффициенту усиления.

Комплексная частотная характеристика

.

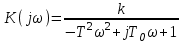Действительная и мнимая частотные характеристики

,

.

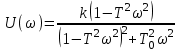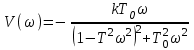Амплитуда



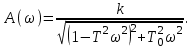
Последнее выражение показывает, что амплитудная частотная характеристика резко отличается от таковой для колебательного звена, рис. 3.10. При ω = 0 значение амплитуды равно k. С увеличением частоты амплитуда уменьшается до нуля. То есть, это монотонная кривая.

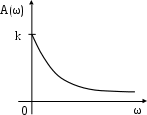
Рис. 3.10. Амплитудная частотная характеристика

апериодического звена второго порядка
Аналогично колебательному звену, фазовая частотная характеристика в интервале 0  ω  1/T рассчитывается по формуле



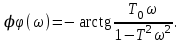
В интервале 1/T  ω  ∞ используется формула



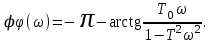
Для апериодического звена асимптотическая логарифмическая амплитудная частотная характеристика получается такой же, как на рис. 3.9.

Переходная функция получается решением уравнения (3.7) при условии x = 1:



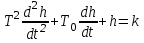
и начальных условиях h = 0, dh/dt = 0 при t = 0.

Характеристическое уравнение



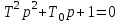
имеет корни

.

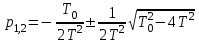Они действительные и отрицательные так как в силу условия апериодичности звена T₀ > 2T.

Переходная функция получается в виде:

.

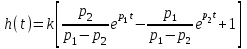При t = 0 h(t) = 0. С увеличением t кривая монотонно стремится к пределу h = k.

Апериодическое звено второго порядка можно назвать типовым условно, потому что такая же математическая модель реализуется двумя инерционными звеньями, соединенными последовательно, рис. 3.11.

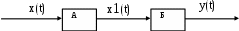
Рис. 3.11. Два последовательно соединенных инерционных звена
Чтобы показать это достаточно, исходя из дифференциальных уравнений звеньев А и Б, получить дифференциальное уравнение (3.7).

---

Пусть уравнения звеньев имеют вид

А

Б

, .

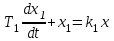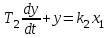Выделим из уравнения Б переменную x₁, продифференцируем по t и заменим соответствующие величины в уравнении А. Это приводит к выражению



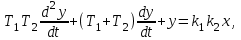
где x, y- входная и выходная величина системы из двух инерционных звеньев. Обозначая T₁T₂ = T², T₁ + T₂ = T₀, k₁k₂ = k, получаем уравнение (3.7):

.

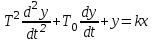3.8. Классификация типовых звеньев
Типовые звенья классифицируется по виду передаточных функций.

1. Устойчивые звенья. Передаточные функции имеют сомножители:

k; pⁿ; 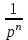; Tp + 1; T²p²+1;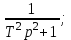

T²p² + T₀p + 1;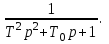

2. Неустойчивые звенья. Передаточные функции имеют сомножители:

Tp – 1; 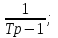T²p² – 1; 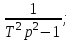T² p² – T₀p +1;

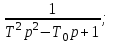T²p² + T₀p – 1; .

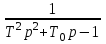3. Запаздывающие звенья. Передаточные функции имеют сомножители:

.

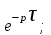
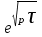4. Трансцендентное звено. Передаточная функция

.

---
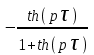