Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 272
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
t) = u(t) – y(t). Сигнал рассогласования может быть отрицательным или положительным, смотря по тому, больше регулируемая величина y(t) чем задаваемая u(t) или меньше. При любом неравенстве на усилитель У и далее на исполнительный механизм ИМ поступает сигнал, по знаку противоположный регулируемой величине. Получается, что управляющее устройство вырабатывает сигнал, обратный по знаку воздействия внешнего возмущения z(t). Тем самым действие возмущения нейтрализуется, процесс возвращается к норме, регулируемый параметр y(t) становится тем, который отвечает назначению.
1.3. Принципы управления
По отклонению. Воздействие на объект вырабатывается как функция отклонения управляемой величины от предписанного значения. Регистрируется отклонение управляемой величины y(t) от заданного значения u(t), рис. 1.2. Управляющее устройство сравнивает значения y(t) и u(t), вырабатывает регулирующее воздействие x(t) и устраняет рассогласование. То есть, как было описано при анализе работы функциональной схемы на рис. 1.3. Регулирующее воздействие осуществляется независимо от числа, природы и места появления возмущений. На практике системы с таким управлением получили преимущественное распространение.
Отметим: системы регулирования по отклонению являются замкнутыми.
По возмущению. Воздействие на объект вырабатывается как компенсирующее отрицательное воздействие возмущений. Из действующих на систему возмущений выбирают основное (оно должно быть измеряемым). Управляющее устройство сравнивает возмущающий сигнал z(t) с задаваемым u(t) и формирует регулирующее воздействие x(t) на объект. Чем достигается компенсация помехи, рис. 1.4.
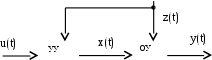
Рис. 1.4. Регулирование по возмущению
Практически регулирование по возмущению не всегда удается организовать, т.к. возмущений обычно несколько и не все можно измерить. Кроме того, система разомкнутая. В управляющее устройство не поступает сигнал о текущем значении регулируемой величины. С течением времени отклонение y(t) от заданного значения может превысить допустимые пределы.
Комбинированное. Регулирование по отклонению и по возмущению осуществляется одновременно, рис. 1.5. В схему вводятся два управляющих устройства: по каналу обратной связи и по каналу возмущения.
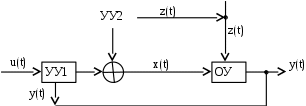
Рис. 1.5. Комбинированное регулирование
Управляющее устройство УУ2 компенсирует отрицательное влияние основного возмущения, а УУ1 – всех других. Комбинированное регулирование позволяет получать высококачественные САР.
Как упоминалось выше, системы с компенсацией разомкнутые. Разомкнутыми могут быть так же системы с программным управлением, в которых требуется изменять управляемую величину заранее предписанным образом. Закон изменения управляемой величины задается программой управляющего устройства или оператором.
Все остальные виды САР выполняются замкнутыми или комбинированными.
Замкнутыми выполняются системы автоматической стабилизации, системы с программным управлением и следящие системы.
В следящих системах значение регулируемой величины заранее неизвестно: это значение является функцией некоторой внешней величины, способной изменяться непредсказуемым способом. Зарегистрировав изменение внешней величины, задающее устройство вырабатывает сигнал на соответствующее изменение регулируемой величины. Работа системы предусматривает постоянное отслеживание поведения внешней величины.
На принципе комбинированного управления создаются системы автоматической стабилизации, следящие, самонастраивающиеся (системы экстремального регулирования). В последних оптимальный режим работы характеризуется экстремальным значением показателя эффективности процесса. Осуществляется автоматический поиск обеспечивающих экстремальность управляющих воздействий.
1.4. Задачи теории
автоматического управления
Основные задачи теории автоматического управления следующие:
- разработка методов анализа САУ;
- разработка методов синтеза САУ;
- разработка принципов построения и методов коррекции динамических свойств САУ.
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – СПБ, «Профессия», 2004. – 752 с.
2. Егоров К.В. Основы теории регулирования. - М.: Энергия, 1967. - 648 с.
3. Востриков А.С., Французова Г.А. Теория автоматического регулирования. – М.: Высшая школа, 2004. – 365 с.
2.1. Дифференциальное и операторное уравнения, передаточная функция
и характеристическое уравнение
разомкнутой системы
Чтобы произвести расчет САУ, надо иметь математическую модель системы. Обычно математической моделью является дифференциальное уравнение, которое получают, анализируя физический, механический или иной процесс.
Рассмотрим математическую модель разомкнутой системы, которая выражается дифференциальным уравнением общего вида:
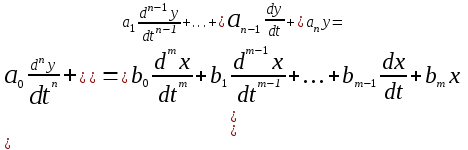(2.1)
где y – управляемая величина, x – управляющая величина; обе – функции времени;коэффициенты ai, bi – постоянные. Правая часть описывает воздействие, левая часть – изменение управляемой величины.
Решение уравнения (2.1) дает полное представление об изменении управляемой величины.
Однако в теории автоматического управления предпочитают иметь дело не с дифференциальным уравнением, а с операторным уравнением, точнее – с его особой формой, которая получила название «передаточная функция».
Операторное уравнение получают, применяя преобразование Лапласа к дифференциальному уравнению.
Суть преобразования Лапласа в том, что функцию от времени преобразуют в функцию от комплексного временного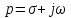
(σ - действительная часть, ω - мнимая часть, j= 
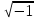). Функцию от времени называют «оригинал», а ее преобразование по Лапласу – «изображение». Для изображения используют прописные буквы.
Символически преобразование Лапласа принято обозначать прописной буквой L. Например,
, 
, 
.
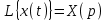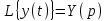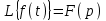
(Читается: «изображение функции x(t) естьX(p) и т. д.)
При преобразовании Лапласа коэффициентымножители не меняются, а изображение производной представляется произведением комплексного переменного p на изображение функции. Например,
, 
.
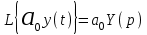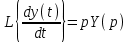Более высокие производные представляются произведением p в соответствующей степени на изображение функции:
, 
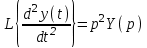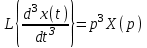и т. п.
Формально оператор дифференцирования заменяется комплексной переменной p в соответствующей степени:
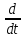на p,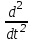 
на p2, 
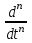на pn .
Преобразование Лапласа, будучи применено к дифференциальному уравнению, преобразует его в алгебраическое. Например,
.
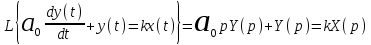Обратный переход из комплексного пространства во временное достигается обратными преобразованием Лапласа, символ L-1. Например,
, 
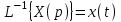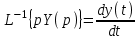и т. д.
.
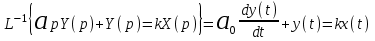В Приложении дана таблица, показывающая преобразование Лапласа некоторых функций.
Применив преобразование Лапласа к дифференциальному уравнению общего вида (2.1), получаем
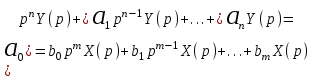
Или
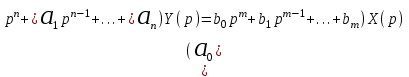(2.2)
Введем обозначения:
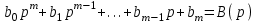, (2.3)
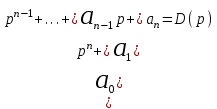(2.4)
Комплексный полином В(р) описывает управляющее воздействие на систему. Комплексный полином D(p) описывает изменение управляемой величины. Введенные обозначения позволяют представить уравнение (2.2) краткой записью:
.
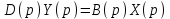
Уравнение (2.2) и его краткую запись называют операторным уравнением.
Особую роль в математическом описании линейных систем автоматического управления играет отношение Y(p)/X(p).Его называют передаточной функцией и обозначают W(p).
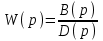. (2.5)
Уточним, что выражение (2.5) является передаточной функцией разомкнутой системы, поскольку получено из дифференциального уравнения (2.1), записанного для разомкнутой системы.
Операторное уравнение можно записывать, используя передаточную функцию:
Y(p) = W(p)X(p). (2.6)
Как было сказано, комплексный полином D(p) описывает изменение управляемой величины. То есть, характеризует процесс, который происходит в системе под влиянием управляющего воздействия. Поэтому полином D(p) называют характеристическим. Приравнивая его к нулю, получают характеристическое уравнение системы:
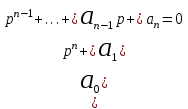. (2.7)
Характеристическое уравнение позволяет найти корни и получить решение дифференциального уравнения. Характеристический полином, характеристическое уравнение служат основой исследования системы на устойчивость.
Для преобразования Лапласа необходимо, чтобы начальные условия были нулевыми, а дифференциальные уравнения – линейными. Однако, линейность уравнений, описывающих реальные технические системы, скорее исключение, чем правило. В случае слабо нелинейной зависимости (типа слабо искривленной линии, участок которой можно заменить прямой с пренебрежимой погрешностью), осуществляют линеаризацию и ведут расчеты на отрезке прямой.
П
ример 2.1.
Записать передаточную функцию и характеристическое уравнение для системы, поведение которой описывается дифференциальным уравнением
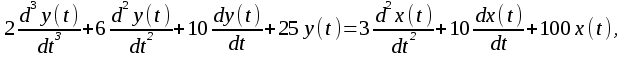
Производим замену символов в дифференциальном уравнении:
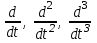на p, p2, p3;
y (t) на Y (p);
x(t) на X(p).
Получаем операторное уравнение:
(2p3 + 6p2 +10p +25) Y(p) = (3p2 + 10p +100)X(p).
Отношение Y(p)/X(p) есть передаточная функция
1.3. Принципы управления
По отклонению. Воздействие на объект вырабатывается как функция отклонения управляемой величины от предписанного значения. Регистрируется отклонение управляемой величины y(t) от заданного значения u(t), рис. 1.2. Управляющее устройство сравнивает значения y(t) и u(t), вырабатывает регулирующее воздействие x(t) и устраняет рассогласование. То есть, как было описано при анализе работы функциональной схемы на рис. 1.3. Регулирующее воздействие осуществляется независимо от числа, природы и места появления возмущений. На практике системы с таким управлением получили преимущественное распространение.
Отметим: системы регулирования по отклонению являются замкнутыми.
По возмущению. Воздействие на объект вырабатывается как компенсирующее отрицательное воздействие возмущений. Из действующих на систему возмущений выбирают основное (оно должно быть измеряемым). Управляющее устройство сравнивает возмущающий сигнал z(t) с задаваемым u(t) и формирует регулирующее воздействие x(t) на объект. Чем достигается компенсация помехи, рис. 1.4.
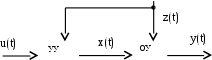
Рис. 1.4. Регулирование по возмущению
Практически регулирование по возмущению не всегда удается организовать, т.к. возмущений обычно несколько и не все можно измерить. Кроме того, система разомкнутая. В управляющее устройство не поступает сигнал о текущем значении регулируемой величины. С течением времени отклонение y(t) от заданного значения может превысить допустимые пределы.
Комбинированное. Регулирование по отклонению и по возмущению осуществляется одновременно, рис. 1.5. В схему вводятся два управляющих устройства: по каналу обратной связи и по каналу возмущения.
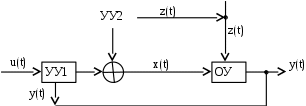
Рис. 1.5. Комбинированное регулирование
Управляющее устройство УУ2 компенсирует отрицательное влияние основного возмущения, а УУ1 – всех других. Комбинированное регулирование позволяет получать высококачественные САР.
Как упоминалось выше, системы с компенсацией разомкнутые. Разомкнутыми могут быть так же системы с программным управлением, в которых требуется изменять управляемую величину заранее предписанным образом. Закон изменения управляемой величины задается программой управляющего устройства или оператором.
Все остальные виды САР выполняются замкнутыми или комбинированными.
Замкнутыми выполняются системы автоматической стабилизации, системы с программным управлением и следящие системы.
В следящих системах значение регулируемой величины заранее неизвестно: это значение является функцией некоторой внешней величины, способной изменяться непредсказуемым способом. Зарегистрировав изменение внешней величины, задающее устройство вырабатывает сигнал на соответствующее изменение регулируемой величины. Работа системы предусматривает постоянное отслеживание поведения внешней величины.
На принципе комбинированного управления создаются системы автоматической стабилизации, следящие, самонастраивающиеся (системы экстремального регулирования). В последних оптимальный режим работы характеризуется экстремальным значением показателя эффективности процесса. Осуществляется автоматический поиск обеспечивающих экстремальность управляющих воздействий.
1.4. Задачи теории
автоматического управления
Основные задачи теории автоматического управления следующие:
- разработка методов анализа САУ;
- разработка методов синтеза САУ;
- разработка принципов построения и методов коррекции динамических свойств САУ.
Литература
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – СПБ, «Профессия», 2004. – 752 с.
2. Егоров К.В. Основы теории регулирования. - М.: Энергия, 1967. - 648 с.
3. Востриков А.С., Французова Г.А. Теория автоматического регулирования. – М.: Высшая школа, 2004. – 365 с.
2.1. Дифференциальное и операторное уравнения, передаточная функция
и характеристическое уравнение
разомкнутой системы
Чтобы произвести расчет САУ, надо иметь математическую модель системы. Обычно математической моделью является дифференциальное уравнение, которое получают, анализируя физический, механический или иной процесс.
Рассмотрим математическую модель разомкнутой системы, которая выражается дифференциальным уравнением общего вида:
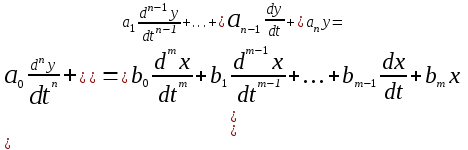(2.1)где y – управляемая величина, x – управляющая величина; обе – функции времени;коэффициенты ai, bi – постоянные. Правая часть описывает воздействие, левая часть – изменение управляемой величины.
Решение уравнения (2.1) дает полное представление об изменении управляемой величины.
Однако в теории автоматического управления предпочитают иметь дело не с дифференциальным уравнением, а с операторным уравнением, точнее – с его особой формой, которая получила название «передаточная функция».
Операторное уравнение получают, применяя преобразование Лапласа к дифференциальному уравнению.
Суть преобразования Лапласа в том, что функцию от времени преобразуют в функцию от комплексного временного
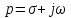(σ - действительная часть, ω - мнимая часть, j= 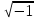). Функцию от времени называют «оригинал», а ее преобразование по Лапласу – «изображение». Для изображения используют прописные буквы.Символически преобразование Лапласа принято обозначать прописной буквой L. Например,
, ,
.
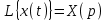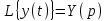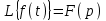
(Читается: «изображение функции x(t) естьX(p) и т. д.)
При преобразовании Лапласа коэффициентымножители не меняются, а изображение производной представляется произведением комплексного переменного p на изображение функции. Например,
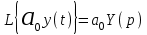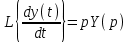, .Более высокие производные представляются произведением p в соответствующей степени на изображение функции:
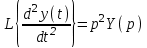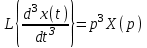, и т. п.Формально оператор дифференцирования заменяется комплексной переменной p в соответствующей степени:
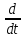на p, 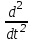на p2, 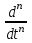на pn .Преобразование Лапласа, будучи применено к дифференциальному уравнению, преобразует его в алгебраическое. Например,
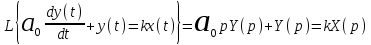.Обратный переход из комплексного пространства во временное достигается обратными преобразованием Лапласа, символ L-1. Например,
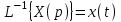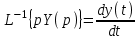, и т. д. 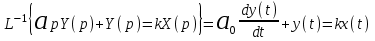.В Приложении дана таблица, показывающая преобразование Лапласа некоторых функций.
Применив преобразование Лапласа к дифференциальному уравнению общего вида (2.1), получаем
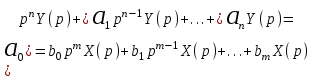
Или
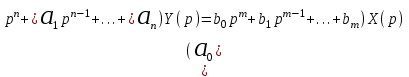(2.2)Введем обозначения:
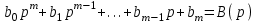, (2.3) 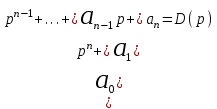(2.4)Комплексный полином В(р) описывает управляющее воздействие на систему. Комплексный полином D(p) описывает изменение управляемой величины. Введенные обозначения позволяют представить уравнение (2.2) краткой записью:
.
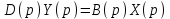
Уравнение (2.2) и его краткую запись называют операторным уравнением.
Особую роль в математическом описании линейных систем автоматического управления играет отношение Y(p)/X(p).Его называют передаточной функцией и обозначают W(p).
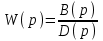. (2.5)Уточним, что выражение (2.5) является передаточной функцией разомкнутой системы, поскольку получено из дифференциального уравнения (2.1), записанного для разомкнутой системы.
Операторное уравнение можно записывать, используя передаточную функцию:
Y(p) = W(p)X(p). (2.6)
Как было сказано, комплексный полином D(p) описывает изменение управляемой величины. То есть, характеризует процесс, который происходит в системе под влиянием управляющего воздействия. Поэтому полином D(p) называют характеристическим. Приравнивая его к нулю, получают характеристическое уравнение системы:
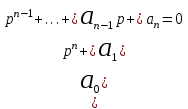. (2.7)Характеристическое уравнение позволяет найти корни и получить решение дифференциального уравнения. Характеристический полином, характеристическое уравнение служат основой исследования системы на устойчивость.
Для преобразования Лапласа необходимо, чтобы начальные условия были нулевыми, а дифференциальные уравнения – линейными. Однако, линейность уравнений, описывающих реальные технические системы, скорее исключение, чем правило. В случае слабо нелинейной зависимости (типа слабо искривленной линии, участок которой можно заменить прямой с пренебрежимой погрешностью), осуществляют линеаризацию и ведут расчеты на отрезке прямой.
П
ример 2.1.
Записать передаточную функцию и характеристическое уравнение для системы, поведение которой описывается дифференциальным уравнением
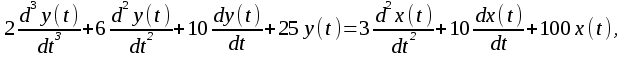
Производим замену символов в дифференциальном уравнении:
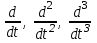на p, p2, p3;y (t) на Y (p);
x(t) на X(p).
Получаем операторное уравнение:
(2p3 + 6p2 +10p +25) Y(p) = (3p2 + 10p +100)X(p).
Отношение Y(p)/X(p) есть передаточная функция