Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 280
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Они могут быть как действительными (4kT < 1), так и комплексными (4kT > 1).
5.2. Критерий Гурвица
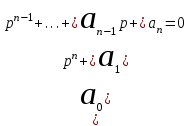 .
.
составляется специальный определитель по следующему правилу.
Намечают n строк и n столбцов (n – степень характеристического уравнения). В первый строке ставят все нечетные коэффициенты: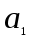 ,
, 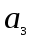 ,
, 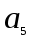 , . . . По главной диагонали, начиная с коэффициента
, . . . По главной диагонали, начиная с коэффициента 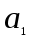 , слева-вниз-направо располагают последовательно все остальные коэффициенты. Столбцы, начиная с главной диагонали, заполняются вверх по нарастающим индексам, вниз - по убывающим. Все коэффициенты с индексами ниже нуля и выше степени уравнения, заменяют нулями. Получается определитель n-го порядка:
, слева-вниз-направо располагают последовательно все остальные коэффициенты. Столбцы, начиная с главной диагонали, заполняются вверх по нарастающим индексам, вниз - по убывающим. Все коэффициенты с индексами ниже нуля и выше степени уравнения, заменяют нулями. Получается определитель n-го порядка:
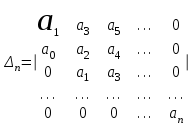
Определитель Δn , а так же определители
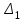 ,
, 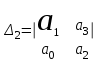 ,
, 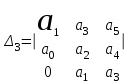 , . . . ,
, . . . ,
называют определителями Гурвица.
Для устойчивости системы необходимо и достаточно, чтобы были положительными все коэффициенты и все определители характеристического уравнения системы:
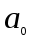 ,
, 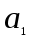 ,
, 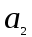 , …,
, …, 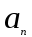 > 0,
> 0, 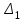 ,
, 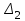 ,
, 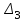 , …,
, …, 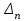 > 0.
> 0.
Получим условия устойчивости для конкретных уравнений.
1. Характеристическое уравнение 2-й степени:
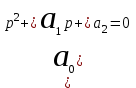 .
.
Ему соответствует определитель Гурвица 2-го порядка:
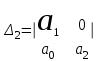 =
= 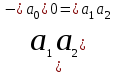 .
.
Условие устойчивости: ,
,  ,
,  > 0, все коэффициенты должны быть положительными.
> 0, все коэффициенты должны быть положительными.
2. Характеристическое уравнение 3-й степени:
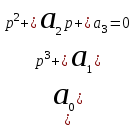 .
.
Ему соответствует определитель Гурвица 3-го порядка:
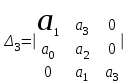 =
= 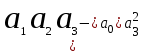 .
.
Определитель =
= 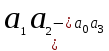 . Неравенство
. Неравенство 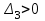 , после сокращения на
, после сокращения на  , получает вид
, получает вид 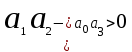 . То есть,
. То есть, 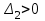 . Условиями устойчивости будут:
. Условиями устойчивости будут: 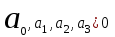 ,
, 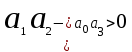 .
.
3. Характеристическое уравнение 4-й степени:
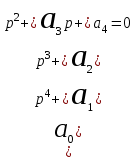 .
.
Ему соответствует определитель Гурвица 4-го порядка:
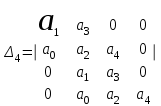 =
= 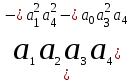 .
.
Определители второго и третьего порядков имеют вид:
 =
= 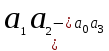 ,
,
 =
= 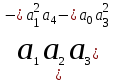 .
.
Неравенство , после сокращения на а4, получает вид
, после сокращения на а4, получает вид 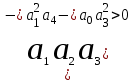 . То есть,
. То есть, 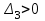
. Значит, условиями устойчивости будут: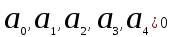 ,
, 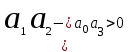 ,
,  .
.
4. Характеристическое уравнение 5-й степени:
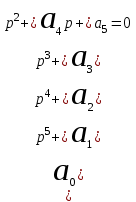 .
.
Опуская процедуру вычисления определителя, выпишем сразу условия устойчивости:
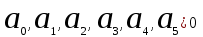 ,
,
 =
= 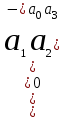 ,
,
Δ4 =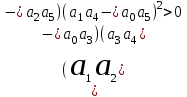 .
.
Можно показать, что при соблюдении этих неравенств неравенства > 0 и
> 0 и 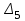 > 0 всегда выполняются. Поэтому их не включают в условия устойчивости системы пятой степени.
> 0 всегда выполняются. Поэтому их не включают в условия устойчивости системы пятой степени.
Можно составлять определители Гурвица и для характеристических уравнений более высокой степени, получая соответствующие условия устойчивости. Однако, объем вычислений нарастает с увеличением степени характеристического уравнения, поэтому считается приемлемым пользоваться критерием Гурвица для характеристических уравнений степени не выше пятой.
Определитель Гурвица позволяет найти коэффициент усиления на границе устойчивости. Коэффициент усиления – это свободный член характеристического уравнения, его индекс равен степени уравнения. Границей устойчивости будет условие Δn-1 = 0. Откуда и вычисляется коэффициент усиления.
П

ример 5.3.
Дана система, характеристическое уравнение которой имеет вид:
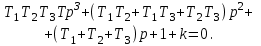
Выяснить, будет ли система устойчивой, если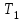 = 1,
= 1, 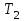 = 2,
= 2, 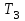
= 3, k= 19? Каким должен быть коэффициент усиления на границе устойчивости?
Записываем характеристическое уравнение 3-й степени в общем виде, сопоставляем его с заданным и заключаем:
 =
= 

 ,
,  =
=  +
+ +
+ ,
,
 =
= 
 +
+
 +
+
 ,
,  =1+k.
=1+k.
Все коэффициенты больше нуля, но надо проверить, будет ли определитель Гурвица больше нуля. Подставив числа в неравенство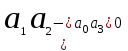 , обнаруживаем, что оно не выполняется: 66 - 120 < 0. Определитель оказался отрицательным. Следовательно, система неустойчива.
, обнаруживаем, что оно не выполняется: 66 - 120 < 0. Определитель оказался отрицательным. Следовательно, система неустойчива.
На границе устойчивости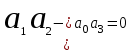 . Подставляя числа, имеем: 11 · 6 = 6 (1 + k). Коэффициент усиления на границе устойчивости k = 10.
. Подставляя числа, имеем: 11 · 6 = 6 (1 + k). Коэффициент усиления на границе устойчивости k = 10.

Пример 5.4.
Выяснить, будет ли устойчивой система с характеристическим уравнением
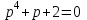 .
.
Сопоставив данное уравнение с его общим видом
Они могут быть как действительными (4kT < 1), так и комплексными (4kT > 1).
5.2. Критерий Гурвица
Для характеристического уравнения
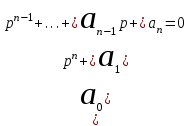 .
.составляется специальный определитель по следующему правилу.
Намечают n строк и n столбцов (n – степень характеристического уравнения). В первый строке ставят все нечетные коэффициенты:
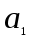 ,
, 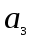 ,
, 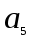 , . . . По главной диагонали, начиная с коэффициента
, . . . По главной диагонали, начиная с коэффициента 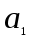 , слева-вниз-направо располагают последовательно все остальные коэффициенты. Столбцы, начиная с главной диагонали, заполняются вверх по нарастающим индексам, вниз - по убывающим. Все коэффициенты с индексами ниже нуля и выше степени уравнения, заменяют нулями. Получается определитель n-го порядка:
, слева-вниз-направо располагают последовательно все остальные коэффициенты. Столбцы, начиная с главной диагонали, заполняются вверх по нарастающим индексам, вниз - по убывающим. Все коэффициенты с индексами ниже нуля и выше степени уравнения, заменяют нулями. Получается определитель n-го порядка: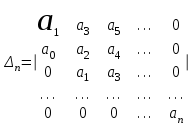
Определитель Δn , а так же определители
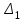 ,
, 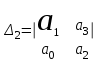 ,
, 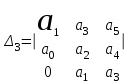 , . . . ,
, . . . ,называют определителями Гурвица.
Для устойчивости системы необходимо и достаточно, чтобы были положительными все коэффициенты и все определители характеристического уравнения системы:
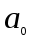 ,
, 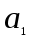 ,
, 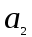 , …,
, …, 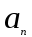 > 0,
> 0, 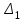 ,
, 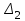 ,
, 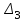 , …,
, …, 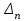 > 0.
> 0.Получим условия устойчивости для конкретных уравнений.
1. Характеристическое уравнение 2-й степени:
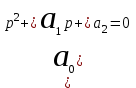 .
.Ему соответствует определитель Гурвица 2-го порядка:
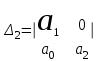 =
= 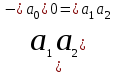 .
.Условие устойчивости:
 ,
,  ,
,  > 0, все коэффициенты должны быть положительными.
> 0, все коэффициенты должны быть положительными.2. Характеристическое уравнение 3-й степени:
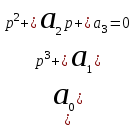 .
.Ему соответствует определитель Гурвица 3-го порядка:
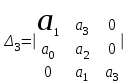 =
= 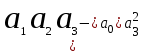 .
.Определитель
 =
= 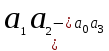 . Неравенство
. Неравенство 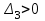 , после сокращения на
, после сокращения на  , получает вид
, получает вид 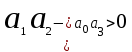 . То есть,
. То есть, 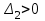 . Условиями устойчивости будут:
. Условиями устойчивости будут: 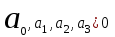 ,
, 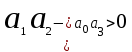 .
.3. Характеристическое уравнение 4-й степени:
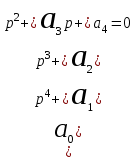 .
.Ему соответствует определитель Гурвица 4-го порядка:
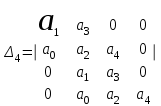 =
= 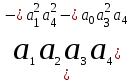 .
.Определители второго и третьего порядков имеют вид:
 =
= 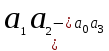 ,
, =
= 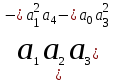 .
.Неравенство
 , после сокращения на а4, получает вид
, после сокращения на а4, получает вид 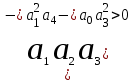 . То есть,
. То есть, 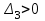
. Значит, условиями устойчивости будут:
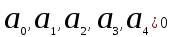 ,
, 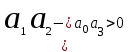 ,
,  .
.4. Характеристическое уравнение 5-й степени:
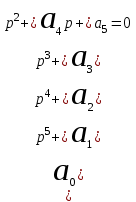 .
.Опуская процедуру вычисления определителя, выпишем сразу условия устойчивости:
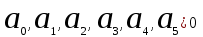 ,
, =
= 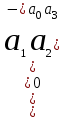 ,
,Δ4 =
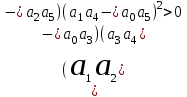 .
.Можно показать, что при соблюдении этих неравенств неравенства
 > 0 и
> 0 и 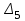 > 0 всегда выполняются. Поэтому их не включают в условия устойчивости системы пятой степени.
> 0 всегда выполняются. Поэтому их не включают в условия устойчивости системы пятой степени.Можно составлять определители Гурвица и для характеристических уравнений более высокой степени, получая соответствующие условия устойчивости. Однако, объем вычислений нарастает с увеличением степени характеристического уравнения, поэтому считается приемлемым пользоваться критерием Гурвица для характеристических уравнений степени не выше пятой.
Определитель Гурвица позволяет найти коэффициент усиления на границе устойчивости. Коэффициент усиления – это свободный член характеристического уравнения, его индекс равен степени уравнения. Границей устойчивости будет условие Δn-1 = 0. Откуда и вычисляется коэффициент усиления.
П

ример 5.3.
Дана система, характеристическое уравнение которой имеет вид:
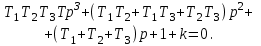
Выяснить, будет ли система устойчивой, если
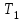 = 1,
= 1, 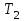 = 2,
= 2, 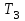
= 3, k= 19? Каким должен быть коэффициент усиления на границе устойчивости?
Записываем характеристическое уравнение 3-й степени в общем виде, сопоставляем его с заданным и заключаем:
 =
= 

 ,
,  =
=  +
+ +
+ ,
, =
= 
 +
+
 +
+
 ,
,  =1+k.
=1+k.Все коэффициенты больше нуля, но надо проверить, будет ли определитель Гурвица больше нуля. Подставив числа в неравенство
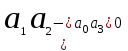 , обнаруживаем, что оно не выполняется: 66 - 120 < 0. Определитель оказался отрицательным. Следовательно, система неустойчива.
, обнаруживаем, что оно не выполняется: 66 - 120 < 0. Определитель оказался отрицательным. Следовательно, система неустойчива.На границе устойчивости
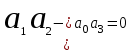 . Подставляя числа, имеем: 11 · 6 = 6 (1 + k). Коэффициент усиления на границе устойчивости k = 10.
. Подставляя числа, имеем: 11 · 6 = 6 (1 + k). Коэффициент усиления на границе устойчивости k = 10.
Пример 5.4.
Выяснить, будет ли устойчивой система с характеристическим уравнением
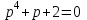 .
.Сопоставив данное уравнение с его общим видом