Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx

Интегральные оценки качества

Первая интегральная оценка:

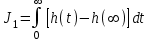. (6.8)

Чем меньше интеграл, тем выше качество регулирования.

Однако, в случае колебательного переходного процесса интеграл (6.8) представляет собой алгебраическую сумму площадей, ограниченных кривой переходного процесса h(t) и прямой h = h(). Отдельные площади суммируются с разными знаками. Интеграл получается минимальным при неудовлетворительном переходном процессе, рис. 6.9. Интеграл (6.8) дает правильное представление о переходном процессе только в случае монотонного хода кривой (например, как на рис. 6.3).

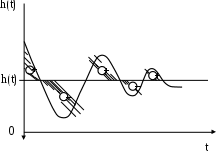
Рис. 6.9. Площади, которые учитывает интеграл (6.8)
Вторая интегральная оценка:

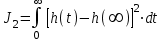. (6.9)

(Интегральная квадратичная ошибка регулирования).

Интеграл (6.9) тоже суммирует площади, расположенные над и под абсциссой h = h(∞). Но в силу квадратичности функции, все слагаемые положительные.

Чем меньше интеграл J₂, тем выше качество регулирования.

Преимущество интегральной оценки J₂ в том, что она применима к колебательным процессам.

Третья интегральная оценка учитывает плавность протекания процесса.

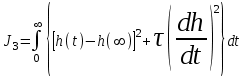. (6.10)

τ– постоянная, имеющая размерность времени. Плавность измерения регулируемого параметра достигается за счетпроизводной dh/dt.

Третья интегральная оценка применима для характеристики как монотонного, так и колебательного процесса. Неудобство применения оценки (6.10) в том, что должна быть заранее известна постоянная τ.

6.3. Чувствительность

к изменению параметров
Объект управления подвержен влиянию окружающей среды, старению, износу. В процессе регулирования эти факторы приводят к отклонению выходной величины от желаемого значения. Иными словами система проявляет чувствительность к изменению своих параметров. В тех случаях, когда важно знать, насколько велика эта чувствительность

---

, ее необходимо оценить.

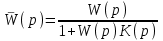. (6.11)

Предположим, значение 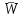изменится на величину 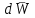. Запишем относительное изменение передаточной функции замкнутой системы:

.

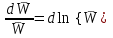Аналогично запишем относительное изменение передаточной функции разомкнутой системы:

.

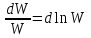Чувствительность САР к изменению передаточной функции разомкнутой системы определяется как отношение относительного изменения передаточной функции замкнутой системы к относительному изменению передаточной функции разомкнутой системы. То есть,

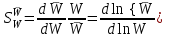. (6.12)

На основании этой формулы легко найти, что чувствительность разомкнутой системы

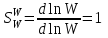. (6.13)

Чувствительность замкнутой системы к изменению передаточной функции звена обратной связи

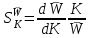. (6.14)

Представим формулу (6.11) в виде

.

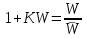Возьмем дифференциал, считая переменными только 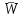и К: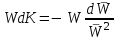

.

Найдем, что 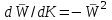и воспользовавшись формулой (6.14), получаем:

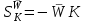. (6.15)

Полученная формула позволяет сделать вывод относительно важной роли звена обратной связи. Действительно, если произведение WK в формуле (6.11) достаточно велико, 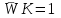, то есть чувствительность становится равной единице. Система реагирует на изменение параметров звена обратной связи как будто она разомкнутая, то есть изменение передаточной функции 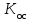непосредственно сказывается на выходной величине. Отсюда практический вывод: звено обратной связи должно обладать стабильными характеристиками, не зависящими от внешних факторов.

---

По формуле (6.12) с помощью формулы (6.11) можно найти, что чувствительность замкнутой системы к изменению передаточной функции объекта равна

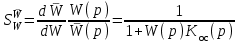. (6.16)

Чувствительность разомкнутой системы

.

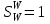Сравнение показывает, что чувствительность замкнутой системы меньше чувствительности разомкнутой системы, так как величина 1 + W(p) K_ос(p) >> 1.

Чувствительность можно определять по отношению к одному из параметров передаточной функции объекта. Пусть параметром, подверженным влиянию внешних факторов, будет λ (это Т или k, или что-то другое).

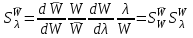. (6.17)
П

ример 6.6.

Передаточная функция разомкнутой системы W = k₁. Выяснить, во сколько раз понизится чувствительность замкнутой системы по сравнению с разомкнутой системой, если включить жесткую обратную связь с коэффициентом усиления k₂? Сделать оценку для k₁ = 100, k₂ = 10.
Чувствительность разомкнутой системы

.

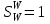Замкнутая система имеет передаточную функцию 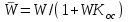. По условию задачи, K_ос = k₂. Чувствительность замкнутой системы, следовательно,

.

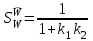Сразу видно, что если k₁ k₂ велико, 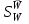мало. Для заданных k₁ и k₂

.

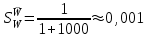То есть в 1000 раз меньше, чем чувствительность разомкнутой системы.

---

Литература

1. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.

2. Востриков А.С., Французова Г.А. Теория автоматического регулирования. – М.: Высшая школа, 2004. – 365 с.

3. Фельдбаум А.А., Бутковский А.Г. Методы теории автоматического управления. – М.: Наука, 1971. – 744 с.

4. Дорф Р., Бишоп Р. Современные системы управления. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.



7.1. Понятие синтеза системы
Теория автоматического управления решает две главные задачи.

Первая – анализ. Система задана: имеется объект управления и управляющее устройство. Требуется найти переходные процессы, которые в ней возникают, выяснить устойчивость и качество.

Вторая – синтез. Система задана не полностью: имеется только объект управления. Требуется разработать управляющее устройство такое, при котором система обладает устойчивостью и удовлетворяет требованиям по качеству.

Однако, не всегда нужно разрабатывать управляющее устройство с нуля. Большей частью принципиальная схема управляющего устройства известна, требуется только приспособить его к системе: внести изменения, поправки. Эта процедура носит название коррекции. В таком случае осуществляют не синтез системы в целом, а лишь синтез корректирующего устройства, входящего в систему.

Рассмотрим основные виды коррекции систем.

7.2. Коррекция систем
Достигается двумя способами.

Первый способ – изменение параметров системы. С изменением параметров меняются коэффициенты уравнений и частотные характеристики, а значит и качество процесса. Но такой подход не всегда осуществим.

Второй способ – изменение структуры системы путем включения дополнительных звеньев, которые называют корректирующими.

7.2.1. Последовательная коррекция
Рассмотрим схему на рис. 7.1.

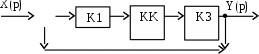
Рис. 7.1. Последовательное включение корректирующего звена
Для замкнутой системы из последовательно соединенных звеньев необходимо получить заданного вида передаточную функцию. Достигается это тем, что между звеньями

---

K₁(p) и K₃(p) включается корректирующее звено K_K(p). Надо найти его передаточную функцию.

Заданная передаточная функция замкнутой системы выражается через передаточную функцию разомкнутой системы формулой

.

Передаточная функция разомкнутой системы содержит в себе передаточную функцию корректирующего звена:

.

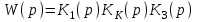Передаточные функции K₁(p) и K₃(p) известны. Введем K₁(p), K_K(p), K₃(p) в 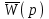и разрешим относительно K_K(p):

.

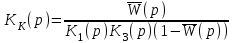Теоретическое выражение найдено. После этого необходимо физически реализовать корректирующее устройство с передаточной функцией K_K(p).

7.2.2. Параллельная коррекция
Рассмотрим схему на рис. 7.2.

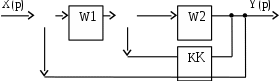
Рис. 7.2. Параллельное включение корректирующего звена
По отношению к схеме ставится задача получить заданного вида передаточную функцию системы путем подсоединения корректирующего звена.

Предварительно находим передаточную функцию разомкнутой системы:

,

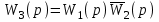где

.

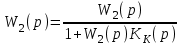Передаточная функция замкнутой системы

.

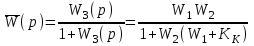По известным передаточным функциям находится передаточная функция корректирующего устройства:

.

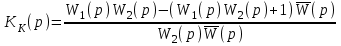7.2.3. Коррекция по возмущению
Рассмотрим схему на рис. 7.3.

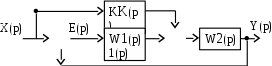
Рис. 7.3. Включение корректирующего звена

в дополнительную прямую связь
Корректирующее устройство включается в дополнительную прямую связь. Управляющий сигнал X(p) по этой связи вводится в систему.

Методом обратного движения находим:

---