Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx

Литература

1. Бесекерский В.А., Попов Е.П. Теория автоматического управления. – СПб, изд-во «Профессия» , 2004 – 752 с.

2. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.

3. Востриков А.С., Французова Г.А.. Теория автоматического регулирования. – М.: Высшая школа, 2004. – 365 с.

4. Фельдбаум А.А., Бутковский А.Г. Методы теории автоматического управления. – М.: Наука, 1971. – 744 с.

5. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. – М.6 Машиностроение, 1973 – 606 с.




Два звена и более, соединенные тем или иным способом, образуют систему. Соединение нескольких звеньев осуществляется линиями (каналами) связи и посредством сумматоров. Совокупность звеньев, сумматоров и линий связи образует структуру системы, т.е. некое упорядоченное расположение составляющих ее частей.

Система заданной структуры характеризуется описывающей ее свойства передаточной функцией. Теория должна дать ответ на вопрос: как, зная структуру, найти передаточную функцию системы? Не менее важно знать ответ и на другой вопрос: как можно изменить структуру того или иного участка системы, сохранив при этом неизменной передаточную функцию системы?
4.1. Построение и анализ

структурных схем
Структурная схема – это графическое представление системы регулирования звеньями с указанием связей между ними. Вместо реальных сигналов рассматриваются их изображения по Лапласу.

Динамическое звено – это элемент, преобразующий сигнал. Имеет математическое описание в виде передаточной функции. Выходящий и входящий сигналы связаны операторным уравнением Y(p) = K(p) X(p), где K(p) – передаточная функция звена.

Сумматор. Элемент, который осуществляет алгебраическое сложение сигналов: X(p) = X₁(p) + X₂(p).

Узел. Элемент, который разветвляет входящий сигнал на идентичные; каждый из отходящих от узла сигналов в точности равен входящему.

Для составления структурных схем приняты следующие обозначения. (Далее аргумент p у функций Y, X, K опускается).

Динамическое звено. Стрелками указывают направление сигнала, то есть обозначают вход и выход.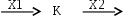
Сумматор. Сигнал Х3 на выходе есть сумма входящих сигналов. Если один из входящих сигналов вычитается, сектор в который он входит, зачерняется или рядом ставят знак «минус».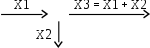
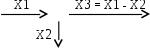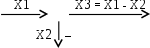Узел. На выходе два и более сигналов, идентичных входящему.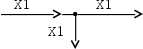
Если надо указать, что в данном месте сигнал меняет знак без изменения величины, то это обозначают тремя способами: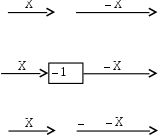

---

Структурная схема, входная и выходная считаются заданными. Ставиться задача определить передаточную функцию системы.

Для определения передаточной функции системы удобно пользоваться методом обратного движения. Метод обратного движения позволяет получить операторное уравнение, из которого и составляется передаточная функция. Заключается он в следующем.

Записывают выходную величину системы Y. Затем, мысленно двигаясь навстречу выходному сигналу, достигают либо звено с передаточной функцией K_n, либо сумматор, либо узел. В случае звена можно записать: Y=K_nX_n-1, где X_n-1– входной сигнал. Продолжая двигаться против направления сигнала, достигают следующее звено с передаточной функцией  K_n - 1 = X_n-1/X_n-2 (X_n-2– входной сигнал этого звена). Исключая X_n-1, получаютоператорное уравнение участка из двух звеньев: Y= K_nK_n-1X_n-2. Если далее в линии нет сумматоров и узлов, то результатом повторения такой процедуры будет операторное уравнение системы: 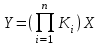, где Х – входной сигнал системы.

Встреча с сумматором означает, что далее надо двигаться по двум (или более) направлениям навстречу сигналам, входящим в сумматор.

Узел, по определению, не меняет сигнал, который в него входит. Проходя через узел, выбирают направление навстречу сигналу. Требование двигаться против направления сигнала сохраняется.

По завершении обратного движения получается операторное уравнение, которое содержит все передаточные функции, регулируемую величину и регулирующую величину. Из операторного уравнения находят передаточную функцию всей системы.

Применяя метод, соблюдают принцип суперпозиции, по которому два сигнала, проходящих по каналу, не взаимодействуют между собой. Их можно сложить и пропустить через звено, или сначала пропустить, а потом сложить  результат будет один и тот же. То есть,

.

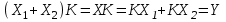4.2. Передаточные функции систем

4.2.1. Последовательное соединение звеньев
Рассмотрим систему из трех последовательно соединенных звеньев с передаточными функциями K₁, K

---

₂, K₃, рис. 4.1.

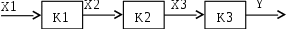
Рис. 4.1. Схема последовательного соединения звеньев
Входная величина системы Х₁, выходная Y. Передаточные функции K₁, K₂, K₃ считаются известными. Надо найти передаточную функцию системы .

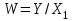Применяя метод обратных движений, выразим Y,X₃,X₂через K₃,K₂,K₁ и последовательно исключим промежуточные сигналы.

.

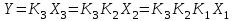Следовательно,

.

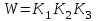Нетрудно вывести для любого числа последовательно соединенных звеньев передаточную функцию системы

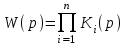. (4.1)

Если какие то группы звеньев соединены заранее, можно найти «групповые» передаточные функции W_iи затем соединить последовательно. Структура формулы для определения передаточной функции системы не измениться:

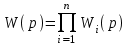. (4.2)






Пример 4.1.

Интегрирующее звено соединяется последовательно с инерционным звеном. Какова будет передаточная функция системы?
Передаточные функции звеньев:

, .

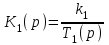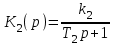Согласно формуле (4.1), передаточная функция системы

,

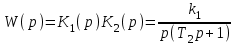где .
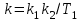П

ример 4.2.

Неустойчивое звено с передаточной функцией

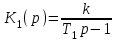последовательно соединяется с неустойчивым звеном, имеющим передаточную функцию .

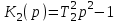Выяснить, при каком условии система будет устойчивой.
Передаточная функция системы

.

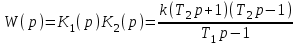Если положить

---

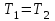
, передаточная функция системы принимает вид: 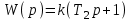. Передаточная функция не содержит знака «минус», что является признаком устойчивости. Значит, условие устойчивости системы .
П

ример 4.3.

Интегрирующее звено соединяется последовательно с реальным дифференцирующим звеном. Найти передаточную функцию.
Передаточные функции звеньев:

, и .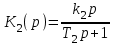

Перемножая, получаем передаточную функцию соединения:

,

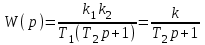где . Она оказалась передаточной функцией инерционного звена.

(Пример показывает, что инерционное звено можно заменить последовательным соединением интегрирующего и реального дифференцирующего звеньев).

4.2.2. Параллельное соединение звеньев
Рассмотрим схему из трех параллельно соединенных звеньев с передаточными функциями K₁, K₂, K₃, рис. 4.2.

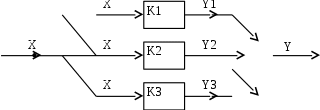
Рис. 4.2. Схема параллельного соединения звеньев
Каждое i-звено имеет одинаковый входной сигнал Х и разные выходные сигналы Y_i. Все входные сигналы звеньев равны входному сигналу системы Х. Выходной сигнал системы равен сумме выходных сигналов звеньев: Y = Y₁ + Y₂ + Y₃. Передаточные функции K₁, K₂, K₃ считаются известными. Надо найти передаточную функцию системы W = Y/X.

Записываем:



.

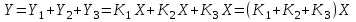
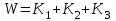Не представляет труда вывести для любого числа параллельно соединенных звеньев передаточную функцию системы:

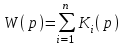. (4.3)

Если параллельно соединяются не звенья, а группы уже соединенных звеньев с передаточными функциямиW_i

---

, то в формулу (4.3) войдут передаточные функции W_i:

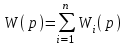. (4.4)
П

ример 4.4.

Пропорционально-интегральный регулятор получают параллельным соединением двух звеньев, уравнения которых

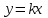и .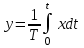

Найти передаточную функцию системы.
Составим операторные уравнения (предварительно продифференцировав второе уравнение, чтобы избавиться от интеграла):

, .

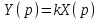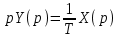Запишем передаточные функции звеньев:

,

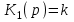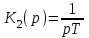
и, следуя формуле (4.3.), получим:

.

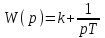П

ример 4.5.

Пропорционально-дифференциальный регулятор образуется параллельным соединением усилительного и идеального дифференцирующего звеньев.

Найти передаточную функцию и дифференциальное уравнение системы.
Запишем передаточные функции звеньев,

,

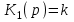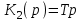
и согласно формуле (4.3.) получим:

.

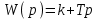Операторное уравнение



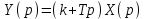
показывает, что дифференциальным уравнением регулятора будет

.

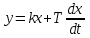4.2.3. Система с обратной связью
Чтобы получить систему с обратной связью, надо соединить звенья параллельно, но с противоположным движением сигналов, как показано на рис. 4.3.

U(p) – сигнал от задающего устройства, в данном случае – входной сигнал системы. С – сумматор.

---