Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 274
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, получаем:
 = 5,
= 5,  =
=  = 0,
= 0,  = 1,
= 1, 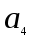 = 2.
= 2.
По условию устойчивости a1 a2 – a0 a3 > 0. Это не выполняется:
-5∙1 < 0. Система неустойчива, хотя все коэффициенты положительные.
П

ример 5.5.
Звенья, передаточные функции которых
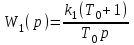 и
и 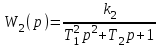 ,
,
соединяются последовательно. Выяснить, будет ли такая система устойчивой? Какую величину имеет постоянная времени T0 на границе устойчивости замкнутой системы?
Находим передаточную функцию разомкнутой системы
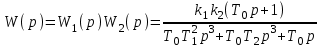 .
.
Ее знаменатель, приравненный к нулю, есть характеристическое уравнение. После сокращения на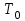 характеристическое уравнение выглядит так:
характеристическое уравнение выглядит так:
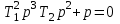 .
.
Сопоставляя с записью характеристического уравнения в общем виде, делаем вывод:
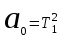 ,
, 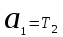 ,
, 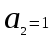 ,
, 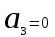 .
.
Для уравнения 3-й степени условия устойчивости требуют, чтобы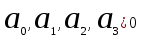 ,
,  .
.
Это соблюдается: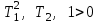 ,
,  – 0
– 0 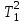 > 0. Следовательно, разомкнутая система устойчива.
> 0. Следовательно, разомкнутая система устойчива.
Составим характеристическое уравнение замкнутой системы. Это будет сумма полиномов числителя и знаменателя, приравненная нулю:
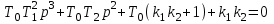 .
.
Выписываем коэффициенты:
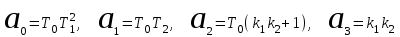 .
.
Выясняем устойчивость:
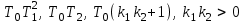 .
.
Замкнутая система будет устойчивой, если
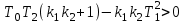 .
.
На границе устойчивости определитель равен нулю, из чего заключаем:
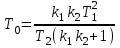 .
.
5.3. Критерий Михайлова
Устойчивость системы выясняется по характеристическому полиному передаточной функции:
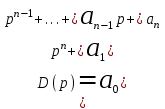 , (2.5)
, (2.5)
где n – степень полинома.
Полагая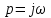 , преобразуем характеристический полином в частотный полином:
, преобразуем характеристический полином в частотный полином:
В зависимости от степени, число (jω)n либо действительное, либо мнимое. По этой причине частотный полином распадается на действительную часть U(ω) и мнимую часть V(ω):
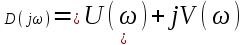 , (5.7)
, (5.7)
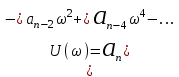 (5.8)
(5.8)
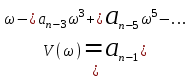 . (5.9)
. (5.9)
U(ω) – четная функция ω, V(ω) – нечетная функция ω. По этому признаку полиномы (5.8) и (5.9) можно назвать «четный» и «нечетный».
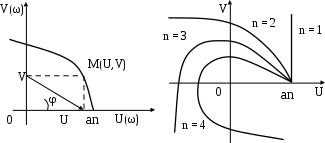
Задавая какое-либо значение частоты ω1, из (5.8) и (5.9) получим числа U(ω1) и V(ω1). Вместе они образуют комплексное число D(jω1). На комплексной плоскости оно обозначается точкой М(U,V), рис. 5.1. Множество точек М(U,V), отвечающих разным частотам, образуют кривую, которая называется годографом Михайлова. Годографы Михайлова имеют разный вид для устойчивых и неустойчивых систем.
Рассмотрим годографы Михайлова для устойчивых систем.
В случае устойчивых систем годограф Михайлова имеет свойство начинаться с точки U(0) = an, V(0) = 0, рис. 5.1. По мере увеличения ωот нуля до бесконечности, точка М(U,V) перемещается влево так, что кривая стремится охватить начало координат, одновременно удаляясь от него. Если провести радиус-вектор из начала координат в точку М(U,V), то окажется, что радиус-вектор будет поворачиваться против часовой стрелки, непрерывно увеличиваясь. Непрерывно увеличивается и угол, который он образует с осью абсцисс. Представив комплексное выражение (5.7) в экспоненциальной форме,
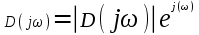 ,
,
обнаруживаем, что радиус-вектор есть модуль частотного полинома |D(jω)|, а угол φ(ω) – аргумент. Модуль имеет величину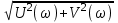 , аргумент равен
, аргумент равен 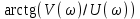 .
.
Вид годографа Михайлова зависит от степени n характеристического полинома (2.5). Годографы полиномов первых четырех степеней показаны на рис. 5.2. Они соответствуют устойчивым системам. Анализ годографов устойчивых систем позволяет сделать выводы, которые и составляют содержание критерия Михайлова.
Можно дать три формулировки критерию Михайлова.
Первая формулировка. Если при изменении частоты от нуля до бесконечности годограф Михайлова начинается на действительной оси в точке an, последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, не проходя через ноль, и уходит в бесконечность в n-м квадранте, - система устойчива.
Вторая формулировка. Если при изменении частоты от нуля до бесконечности вектор комплексного частотного полинома D(jω) последовательно поворачивается против часовой стрелки на угол n(/2), где n – степень характеристического полинома, и нигде не становится нулем, - система устойчива.
Обратим внимание на частоты, при которых годограф пересекает оси координат. Назовем их частоты пересечения. Первая частота нулевая, с нее начинается годограф. При =0 U(0) = an, V(0) = 0. Вторая отвечает точке пересечения годографом положительного отрезка оси ординат, U(
=0 U(0) = an, V(0) = 0. Вторая отвечает точке пересечения годографом положительного отрезка оси ординат, U( ) = 0, V(
) = 0, V( ) – какое-то число. Непрерывно увеличивая частоту, при некоторой, равной
) – какое-то число. Непрерывно увеличивая частоту, при некоторой, равной 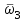 , получим пересечение годографа с отрицательной частью оси абсцисс. Очевидно, четвертым будет пересечение с отрицательной частью оси ординат при частоте
, получим пересечение годографа с отрицательной частью оси абсцисс. Очевидно, четвертым будет пересечение с отрицательной частью оси ординат при частоте 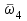 . Далее последуют частоты пересечения
. Далее последуют частоты пересечения 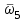 ,
, 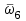 , …,
, …,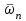 . Все они действительные положительные числа, каждое последующее больше предыдущего.
. Все они действительные положительные числа, каждое последующее больше предыдущего.
Третья формулировка критерия Михайлова: если частоты пересечения годографа с осями координат чередуются и образуют возрастающую последовательность вида
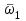 <
< 
< <…
<… ,
,
- система устойчивая.
В отличие от предыдущих, третья формулировка позволяет исследовать устойчивость системы без построения годографа, аналитически. Соображения следующие.
Каждому пересечению годографом действительной оси (когда V(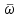 ) = 0) будет соответствовать корень нечетного полинома V(
) = 0) будет соответствовать корень нечетного полинома V(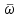 ). Каждому пересечению мнимой оси (когда U(
). Каждому пересечению мнимой оси (когда U(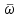 ) = 0) будет соответствовать корень четного полинома U(
) = 0) будет соответствовать корень четного полинома U(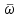 ). Следовательно, по мере увеличения ωкорни полиномов V(
). Следовательно, по мере увеличения ωкорни полиномов V(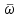 ) и U(
) и U(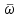 ) для устойчивой системы должны чередоваться (корень полинома V(
) для устойчивой системы должны чередоваться (корень полинома V(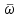 ) сменяется корнем полинома U(
) сменяется корнем полинома U(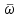 ) и т.д.); корень каждого последующего пересечения оси должен быть больше предыдущего, все корни должны быть действительными. Общее число корней равно степени характеристического полинома.
) и т.д.); корень каждого последующего пересечения оси должен быть больше предыдущего, все корни должны быть действительными. Общее число корней равно степени характеристического полинома.
В случае неустойчивых систем кривые не охватывают начало координат, чередования частот нечетного и четного полиномов нет, рис. 5.3.
Если годограф начинается из начала координат или проходит через начало координат, система находится на границе устойчивости, рис. 5.4.
П

ример 5.6.
Построить годограф Михайлова для характеристического уравнения
2 p + 1 = 0.
 = 5,
= 5,  =
=  = 0,
= 0,  = 1,
= 1, 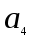 = 2.
= 2.По условию устойчивости a1 a2 – a0 a3 > 0. Это не выполняется:
-5∙1 < 0. Система неустойчива, хотя все коэффициенты положительные.
П

ример 5.5.
Звенья, передаточные функции которых
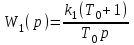 и
и 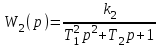 ,
,соединяются последовательно. Выяснить, будет ли такая система устойчивой? Какую величину имеет постоянная времени T0 на границе устойчивости замкнутой системы?
Находим передаточную функцию разомкнутой системы
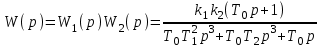 .
.Ее знаменатель, приравненный к нулю, есть характеристическое уравнение. После сокращения на
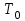 характеристическое уравнение выглядит так:
характеристическое уравнение выглядит так: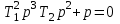 .
.Сопоставляя с записью характеристического уравнения в общем виде, делаем вывод:
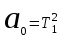 ,
, 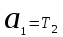 ,
, 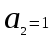 ,
, 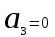 .
.Для уравнения 3-й степени условия устойчивости требуют, чтобы
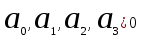 ,
,  .
.Это соблюдается:
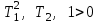 ,
,  – 0
– 0 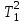 > 0. Следовательно, разомкнутая система устойчива.
> 0. Следовательно, разомкнутая система устойчива.
Составим характеристическое уравнение замкнутой системы. Это будет сумма полиномов числителя и знаменателя, приравненная нулю:
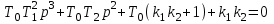 .
.Выписываем коэффициенты:
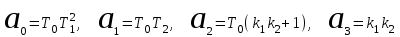 .
. Выясняем устойчивость:
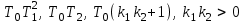 .
.Замкнутая система будет устойчивой, если
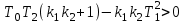 .
.На границе устойчивости определитель равен нулю, из чего заключаем:
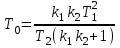 .
.5.3. Критерий Михайлова
Устойчивость системы выясняется по характеристическому полиному передаточной функции:
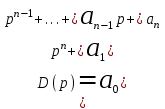 , (2.5)
, (2.5)где n – степень полинома.
Полагая
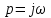 , преобразуем характеристический полином в частотный полином:
, преобразуем характеристический полином в частотный полином: 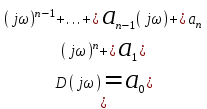 .
.
В зависимости от степени, число (jω)n либо действительное, либо мнимое. По этой причине частотный полином распадается на действительную часть U(ω) и мнимую часть V(ω):
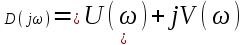 , (5.7)
, (5.7)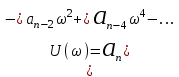 (5.8)
(5.8)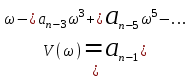 . (5.9)
. (5.9)U(ω) – четная функция ω, V(ω) – нечетная функция ω. По этому признаку полиномы (5.8) и (5.9) можно назвать «четный» и «нечетный».
Задавая какое-либо значение частоты ω1, из (5.8) и (5.9) получим числа U(ω1) и V(ω1). Вместе они образуют комплексное число D(jω1). На комплексной плоскости оно обозначается точкой М(U,V), рис. 5.1. Множество точек М(U,V), отвечающих разным частотам, образуют кривую, которая называется годографом Михайлова. Годографы Михайлова имеют разный вид для устойчивых и неустойчивых систем.
Рассмотрим годографы Михайлова для устойчивых систем.
В случае устойчивых систем годограф Михайлова имеет свойство начинаться с точки U(0) = an, V(0) = 0, рис. 5.1. По мере увеличения ωот нуля до бесконечности, точка М(U,V) перемещается влево так, что кривая стремится охватить начало координат, одновременно удаляясь от него. Если провести радиус-вектор из начала координат в точку М(U,V), то окажется, что радиус-вектор будет поворачиваться против часовой стрелки, непрерывно увеличиваясь. Непрерывно увеличивается и угол, который он образует с осью абсцисс. Представив комплексное выражение (5.7) в экспоненциальной форме,
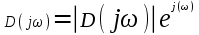 ,
,обнаруживаем, что радиус-вектор есть модуль частотного полинома |D(jω)|, а угол φ(ω) – аргумент. Модуль имеет величину
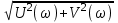 , аргумент равен
, аргумент равен 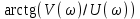 .
.Вид годографа Михайлова зависит от степени n характеристического полинома (2.5). Годографы полиномов первых четырех степеней показаны на рис. 5.2. Они соответствуют устойчивым системам. Анализ годографов устойчивых систем позволяет сделать выводы, которые и составляют содержание критерия Михайлова.
Можно дать три формулировки критерию Михайлова.
Первая формулировка. Если при изменении частоты от нуля до бесконечности годограф Михайлова начинается на действительной оси в точке an, последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, не проходя через ноль, и уходит в бесконечность в n-м квадранте, - система устойчива.

| Рис.5.1. Геометрическое представление частотного полинома D(jω) | Рис. 5.2. Годографы Михайлова для разных степеней полиномов |
Вторая формулировка. Если при изменении частоты от нуля до бесконечности вектор комплексного частотного полинома D(jω) последовательно поворачивается против часовой стрелки на угол n(/2), где n – степень характеристического полинома, и нигде не становится нулем, - система устойчива.
Обратим внимание на частоты, при которых годограф пересекает оси координат. Назовем их частоты пересечения. Первая частота нулевая, с нее начинается годограф. При
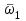 =0 U(0) = an, V(0) = 0. Вторая отвечает точке пересечения годографом положительного отрезка оси ординат, U(
=0 U(0) = an, V(0) = 0. Вторая отвечает точке пересечения годографом положительного отрезка оси ординат, U( ) = 0, V(
) = 0, V( ) – какое-то число. Непрерывно увеличивая частоту, при некоторой, равной
) – какое-то число. Непрерывно увеличивая частоту, при некоторой, равной 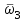 , получим пересечение годографа с отрицательной частью оси абсцисс. Очевидно, четвертым будет пересечение с отрицательной частью оси ординат при частоте
, получим пересечение годографа с отрицательной частью оси абсцисс. Очевидно, четвертым будет пересечение с отрицательной частью оси ординат при частоте 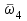 . Далее последуют частоты пересечения
. Далее последуют частоты пересечения 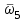 ,
, 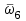 , …,
, …,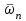 . Все они действительные положительные числа, каждое последующее больше предыдущего.
. Все они действительные положительные числа, каждое последующее больше предыдущего.Третья формулировка критерия Михайлова: если частоты пересечения годографа с осями координат чередуются и образуют возрастающую последовательность вида
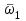 <
< 
<
 <…
<… ,
,- система устойчивая.
В отличие от предыдущих, третья формулировка позволяет исследовать устойчивость системы без построения годографа, аналитически. Соображения следующие.
Каждому пересечению годографом действительной оси (когда V(
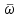 ) = 0) будет соответствовать корень нечетного полинома V(
) = 0) будет соответствовать корень нечетного полинома V(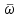 ). Каждому пересечению мнимой оси (когда U(
). Каждому пересечению мнимой оси (когда U(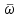 ) = 0) будет соответствовать корень четного полинома U(
) = 0) будет соответствовать корень четного полинома U(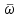 ). Следовательно, по мере увеличения ωкорни полиномов V(
). Следовательно, по мере увеличения ωкорни полиномов V(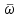 ) и U(
) и U(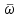 ) для устойчивой системы должны чередоваться (корень полинома V(
) для устойчивой системы должны чередоваться (корень полинома V(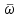 ) сменяется корнем полинома U(
) сменяется корнем полинома U(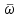 ) и т.д.); корень каждого последующего пересечения оси должен быть больше предыдущего, все корни должны быть действительными. Общее число корней равно степени характеристического полинома.
) и т.д.); корень каждого последующего пересечения оси должен быть больше предыдущего, все корни должны быть действительными. Общее число корней равно степени характеристического полинома.В случае неустойчивых систем кривые не охватывают начало координат, чередования частот нечетного и четного полиномов нет, рис. 5.3.
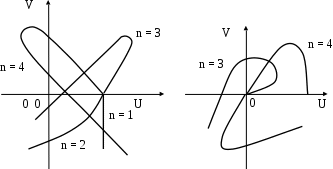
| Рис. 5.3. Годографы Михайлова неустойчивых систем | Рис. 5.4. Годографы Михайлова систем на границе устойчивости |
Если годограф начинается из начала координат или проходит через начало координат, система находится на границе устойчивости, рис. 5.4.
П

ример 5.6.
Построить годограф Михайлова для характеристического уравнения
2 p + 1 = 0.