Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 271
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
1. Монотонные. Первая производная не меняет знак: dh/dtлибо 0, либо 0. Пример на рис. 2.4.
2. Колебательные. dh/dtрегулярноменяет плюс на минус и наоборот. Пример на рис. 2.5.
3. Апериодические. dh/dtменяет знак один раз. Пример на рис. 2.6.
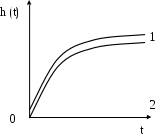
Рис. 2.4. Монотонно меняющиеся кривые
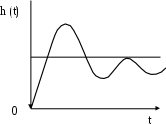
Рис. 2.5. Затухающие колебания
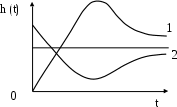
Рис. 2.6. Апериодические кривые
Все функции могут быть получены как решение одного дифференциального уравнения при разном значении его коэффициентов или, что все равно, при разном значении коэффициентов характеристического уравнения. Решение характеристического уравнения общего вида (2.7) дает n корней (комплексных, действительных, мнимых). Общее решение линейного однородного дифференциального уравнения есть сумма n экспонент,
,
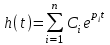где Сi – постоянные интегрирования, pi– корни характеристического уравнения. Действительные корни, p= σ , обеспечивают неограниченный рост или уменьшение до нуля соответствующих экспонент. Комплексные корни, p= σ jω, обеспечивают возрастающие или затухающие колебания. Экспоненты с чисто мнимыми корнями, p = jω, обеспечивают гармонические колебания (колебания с постоянной амплитудой).
В зависимости от коэффициентов, количество тех или иных видов корней будет меняться, что и обеспечивает тот или иной вид кривых переходного процесса.
Аналитическое выражение кривой переходного процесса можно получить двумя путями. Первый – непосредственное решение дифференциального уравнения, описывающего систему. Надо положить величину входного воздействия x = 1 и выполнить нулевые начальные условия. Второй – на основе операторного уравнения. Надо ввести в него изображение единичного ступенчатого воздействия и выполнить обратное преобразование Лапласа.
В некоторых системах автоматического управления важную роль играют импульсные переходные функции. Их получают, подавая на вход системы единичный импульс. Импульсная переходная функция отличается от «ступенчатой», поскольку как было сказано выше, импульсная функция есть производная от ступенчатой:
.
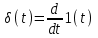Пример 2.5.
Процесс в объекте описывается дифференциальным уравнением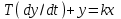
. Найти переходную функцию.
Вводим условие единичного ступенчатого воздействия, полагая x = 1. Ищем решение дифференциального уравнения при нулевых начальных условиях. Решением будет переходная функция h(t), поэтому сразу можно y(t) заменить на h(t).
Общее решение неоднородного уравнения
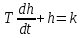
есть сумма решений h1 + h2. Первое получают, решая однородное уравнение
.
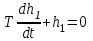Решением будет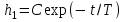
. Второе решение h2 есть частное решение неоднородного уравнения, которое можно выбрать как h2 = k. Общим решением будет:
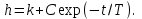
C учетом того, что h = 0 при t = 0, окончательное выражение для переходной функции получается в виде:
.
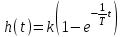П
ример 2.6.
Найти переходную функцию для системы, описываемой дифференциальным уравнением
.
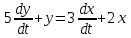Запишем операторное уравнение
(5p + 1) Y(p) = (3p + 2) X(p)
в виде
.
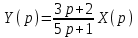Множитель при X(p) есть не что иное, как передаточная функция. X(p) – изображение произвольного воздействия. Воздействие в виде единичного ступенчатого скачка имеет изображение X(p) = 1/p. Если в операторном уравнении заменить X(p) на 1/p, то на Y(p) накладывается требование быть изображением переходной функции. Подчеркивая это, заменим Y(p) на H(p). Получаем операторное уравнение для переходной функции:
.
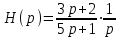Прежде чем воспользоваться таблицей изображений по Лапласу, представим правую часть уравнения в виде суммы:
.
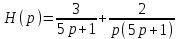В таблице находим оригиналы по их изображениям:
,
,
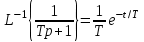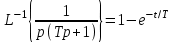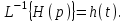
В нашем случае T = 5. Множители 3 и 2 сохраняют свое значение и место. Окончательно
,
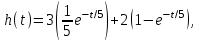или
.
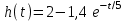1. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.
2. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). – М.: Машиностроение, 1977. – 464 с.
3. Гноенский Л.С., Каменский Г.С., Эльсгольц Л.Э. Математические основы теории управляемых систем. – М.: Наука, 1969.
Системы автоматического регулирования удобно представлять в виде соединения элементов, каждый из которых описывается алгебраическим или дифференциальным уравнением не выше второго порядка. При этом, одно и то же дифференциальное уравнение может описывать разные по своей физической природе элементы. Иными словами, у них одна математическая модель. Наиболее употребительные математические модели получили название типовых звеньев. Типовые звенья имеют одну входную и одну выходную величину.
Все конструктивное разнообразие САР можно представить небольшим числом типовых звеньев или их комбинаций.
Рассмотрим следующие типовые звенья.
Звенья, описываемые алгебраическими уравнениями:
- усилительное (пропорциональное),
- запаздывающее.
Звенья, описываемые дифференциальным уравнением первого порядка:
- инерционное,
- интегрирующее,
- дифференцирующее.
Звено, описываемое дифференциальным уравнением второго порядка. В зависимости от соотношения коэффициентов, оно может быть колебательным или апериодическим.
Характеристики типовых звеньев принято указывать для единичного ступенчатого входного воздействия.
Для полной характеристики типового звена следует указать его дифференциальное уравнение, операторное уравнение, передаточную функцию, комплексную, действительную, мнимую, амплитудную, фазовую, логарифмическую амплитудную, логарифмическую фазовую частотные характеристики и переходную функцию.
У этого звена выходная величина y(t) пропорциональна входной. Поэтому усилительное звено называют еще пропорциональным. Математическая модель
y(t) =
kx(t), (3.1)
где константа k - коэффициент усиления звена.
Операторное уравнение
Y(p) = kX(p).
Передаточная функция представляет собой коэффициент усиления:
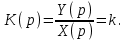
(Здесь и далее передаточную функцию типового звена будем обозначать K(p)).
Комплексная частотная характеристика имеет только действительную часть:
K(jω) = k.
Формально, в соответствие с формулой (2.9), K(jω) = U(ω) + jV(ω). Действительная частотная характеристика U(ω) = k, мнимая частотная характеристика V(ω) = 0.
Амплитудная частотная характеристика:
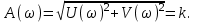
Она не зависит от ω- входной сигнал любой частоты изменяется в k раз.
Фазовая частотная характеристика:
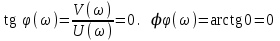
Фазовый сдвиг отсутствует.
Логарифмическая амплитудная частотная характеристика имеет вид:
L (ω) = 20 lg A (ω) = 20 lg k.
От ω, следовательно и от lg ω, не зависит. (Прямая, параллельная оси абсцисс).
Переходную функцию усилительного звена получают, положив x = 1(t) в уравнении y = kx. Переходная функция h(t) = k1(t).
Регулирование объекта осуществляется с помощью устройств, динамические характеристики которых могут быть близкими или идентичными характеристиками типовых звеньев. В частности, используются регуляторы с характеристиками усилительного звена. Их называют П - регуляторы, имея ввиду пропорциональность входной и выходной величин.
3.2. Запаздывающее звено
В запаздывающем звене выходная величина начинает изменяться не мгновенно с воздействием входной величины, а некоторое время τспустя.
Уравнение звена:
y(t) = kx(t- τ), (3.2)
где τ – время запаздывания.
Изображение функции с запаздывающим аргументом x(t – τ) по Лапласу есть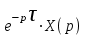
. Следовательно, операторное уравнение будет
.
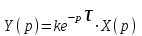Передаточная функция звена
.
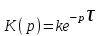Комплексная частотная характеристика, если раскрыть ее формулой Эйлера через тригонометрические функции,
1. Монотонные. Первая производная не меняет знак: dh/dtлибо 0, либо 0. Пример на рис. 2.4.
2. Колебательные. dh/dtрегулярноменяет плюс на минус и наоборот. Пример на рис. 2.5.
3. Апериодические. dh/dtменяет знак один раз. Пример на рис. 2.6.
Рис. 2.4. Монотонно меняющиеся кривые
Рис. 2.5. Затухающие колебания
Рис. 2.6. Апериодические кривые
Все функции могут быть получены как решение одного дифференциального уравнения при разном значении его коэффициентов или, что все равно, при разном значении коэффициентов характеристического уравнения. Решение характеристического уравнения общего вида (2.7) дает n корней (комплексных, действительных, мнимых). Общее решение линейного однородного дифференциального уравнения есть сумма n экспонент,
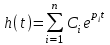,где Сi – постоянные интегрирования, pi– корни характеристического уравнения. Действительные корни, p= σ , обеспечивают неограниченный рост или уменьшение до нуля соответствующих экспонент. Комплексные корни, p= σ jω, обеспечивают возрастающие или затухающие колебания. Экспоненты с чисто мнимыми корнями, p = jω, обеспечивают гармонические колебания (колебания с постоянной амплитудой).
В зависимости от коэффициентов, количество тех или иных видов корней будет меняться, что и обеспечивает тот или иной вид кривых переходного процесса.
Аналитическое выражение кривой переходного процесса можно получить двумя путями. Первый – непосредственное решение дифференциального уравнения, описывающего систему. Надо положить величину входного воздействия x = 1 и выполнить нулевые начальные условия. Второй – на основе операторного уравнения. Надо ввести в него изображение единичного ступенчатого воздействия и выполнить обратное преобразование Лапласа.
В некоторых системах автоматического управления важную роль играют импульсные переходные функции. Их получают, подавая на вход системы единичный импульс. Импульсная переходная функция отличается от «ступенчатой», поскольку как было сказано выше, импульсная функция есть производная от ступенчатой:
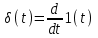. Пример 2.5.
Процесс в объекте описывается дифференциальным уравнением
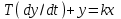. Найти переходную функцию.Вводим условие единичного ступенчатого воздействия, полагая x = 1. Ищем решение дифференциального уравнения при нулевых начальных условиях. Решением будет переходная функция h(t), поэтому сразу можно y(t) заменить на h(t).
Общее решение неоднородного уравнения
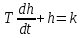
есть сумма решений h1 + h2. Первое получают, решая однородное уравнение
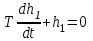.Решением будет
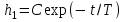. Второе решение h2 есть частное решение неоднородного уравнения, которое можно выбрать как h2 = k. Общим решением будет: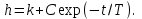 C учетом того, что h = 0 при t = 0, окончательное выражение для переходной функции получается в виде:
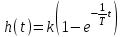.П
ример 2.6.
Найти переходную функцию для системы, описываемой дифференциальным уравнением
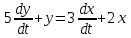.Запишем операторное уравнение
(5p + 1) Y(p) = (3p + 2) X(p)
в виде
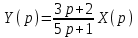.Множитель при X(p) есть не что иное, как передаточная функция. X(p) – изображение произвольного воздействия. Воздействие в виде единичного ступенчатого скачка имеет изображение X(p) = 1/p. Если в операторном уравнении заменить X(p) на 1/p, то на Y(p) накладывается требование быть изображением переходной функции. Подчеркивая это, заменим Y(p) на H(p). Получаем операторное уравнение для переходной функции:
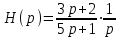.Прежде чем воспользоваться таблицей изображений по Лапласу, представим правую часть уравнения в виде суммы:
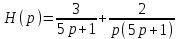.В таблице находим оригиналы по их изображениям:
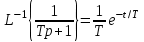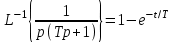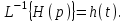
, , В нашем случае T = 5. Множители 3 и 2 сохраняют свое значение и место. Окончательно
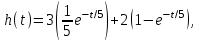,или
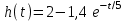.Литература
1. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.
2. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). – М.: Машиностроение, 1977. – 464 с.
3. Гноенский Л.С., Каменский Г.С., Эльсгольц Л.Э. Математические основы теории управляемых систем. – М.: Наука, 1969.
Системы автоматического регулирования удобно представлять в виде соединения элементов, каждый из которых описывается алгебраическим или дифференциальным уравнением не выше второго порядка. При этом, одно и то же дифференциальное уравнение может описывать разные по своей физической природе элементы. Иными словами, у них одна математическая модель. Наиболее употребительные математические модели получили название типовых звеньев. Типовые звенья имеют одну входную и одну выходную величину.
Все конструктивное разнообразие САР можно представить небольшим числом типовых звеньев или их комбинаций.
Рассмотрим следующие типовые звенья.
Звенья, описываемые алгебраическими уравнениями:
- усилительное (пропорциональное),
- запаздывающее.
Звенья, описываемые дифференциальным уравнением первого порядка:
- инерционное,
- интегрирующее,
- дифференцирующее.
Звено, описываемое дифференциальным уравнением второго порядка. В зависимости от соотношения коэффициентов, оно может быть колебательным или апериодическим.
Характеристики типовых звеньев принято указывать для единичного ступенчатого входного воздействия.
Для полной характеристики типового звена следует указать его дифференциальное уравнение, операторное уравнение, передаточную функцию, комплексную, действительную, мнимую, амплитудную, фазовую, логарифмическую амплитудную, логарифмическую фазовую частотные характеристики и переходную функцию.
3.1 Усилительное звено
У этого звена выходная величина y(t) пропорциональна входной. Поэтому усилительное звено называют еще пропорциональным. Математическая модель
y(t) =
kx(t), (3.1)
где константа k - коэффициент усиления звена.
Операторное уравнение
Y(p) = kX(p).
Передаточная функция представляет собой коэффициент усиления:
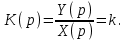
(Здесь и далее передаточную функцию типового звена будем обозначать K(p)).
Комплексная частотная характеристика имеет только действительную часть:
K(jω) = k.
Формально, в соответствие с формулой (2.9), K(jω) = U(ω) + jV(ω). Действительная частотная характеристика U(ω) = k, мнимая частотная характеристика V(ω) = 0.
Амплитудная частотная характеристика:
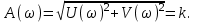
Она не зависит от ω- входной сигнал любой частоты изменяется в k раз.
Фазовая частотная характеристика:
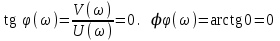
Фазовый сдвиг отсутствует.
Логарифмическая амплитудная частотная характеристика имеет вид:
L (ω) = 20 lg A (ω) = 20 lg k.
От ω, следовательно и от lg ω, не зависит. (Прямая, параллельная оси абсцисс).
Переходную функцию усилительного звена получают, положив x = 1(t) в уравнении y = kx. Переходная функция h(t) = k1(t).
Регулирование объекта осуществляется с помощью устройств, динамические характеристики которых могут быть близкими или идентичными характеристиками типовых звеньев. В частности, используются регуляторы с характеристиками усилительного звена. Их называют П - регуляторы, имея ввиду пропорциональность входной и выходной величин.
3.2. Запаздывающее звено
В запаздывающем звене выходная величина начинает изменяться не мгновенно с воздействием входной величины, а некоторое время τспустя.
Уравнение звена:
y(t) = kx(t- τ), (3.2)
где τ – время запаздывания.
Изображение функции с запаздывающим аргументом x(t – τ) по Лапласу есть
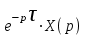. Следовательно, операторное уравнение будет 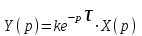.Передаточная функция звена
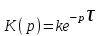.Комплексная частотная характеристика, если раскрыть ее формулой Эйлера через тригонометрические функции,