Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx
Добавлен: 12.01.2024
Просмотров: 202
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Критерии оценки:
«5» ставится за 4 верно решенных заданий;
«4» ставится за 3 верно решенных задания;
«3» ставится за 2 верно решенных задания;
«2» - если решено менее 2 заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 3.1. Основные тригонометрические тождества
Практическая работа № 14
Формулы двойных и половинных аргументов.
Цель: закрепление знаний, отработка навыков работы с формулами тригонометрии.
Пояснения к работе.
Основные формулы: (1)
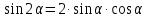 ,
, (2)
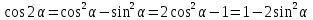
(3) tg 2
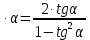
(4)
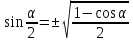
(5)
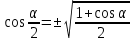
(6)
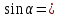
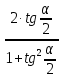 (7)
(7) 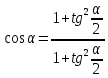
Пример 1. Упростите выражение:
2
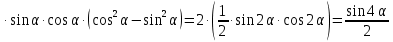
Пример 2. Упростите выражение:
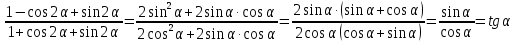
Задания к практической работе.
| Вариант 1 | Вариант 2 |
| 1) 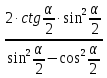 - - упростить упростить | 1) 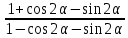 - - упростить упростить |
| 2) 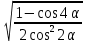 - - упростить упростить | 2) 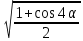  - - упростить упростить |
| 3) Доказать 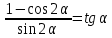 | тождества: 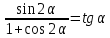 |
| 4  | 4 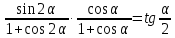 |
| 5 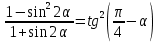 | 5 2 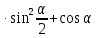 - - упростить упростить |
Критерии оценки:
«5»- ставится за 5 верно решенных задания;
«4» - ставится за 4 верно решенных задания;
«3» - ставится за 2-3 верно решенное задания;
«2» - выполнено менее 2 заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 3.2. Основы тригонометрии.
Практическая работа № 15
Формулы суммы и разности для синуса, косинуса, двойного аргумента для синуса и косинуса и их применение для преобразования выражений.
Цель: способствовать закреплению навыков применения формул для преобразования выражений.
Формулы суммы и разности для синуса и косинуса
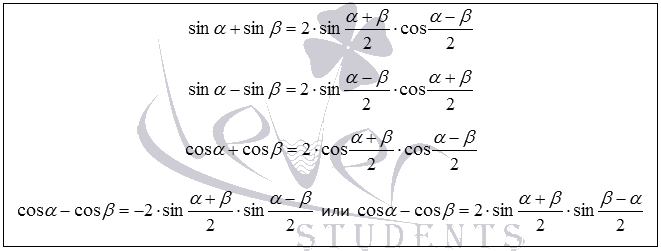
Пример1. Вычислите точное значение разности синусов 165 и 75 градусов.
Точных значений синусов 165 и 75 градусов мы не знаем, поэтому непосредственно вычислить значение заданной разности мы не можем. Но ответить на вопрос задачи нам позволяет формула разности синусов
Таким образом, имеем
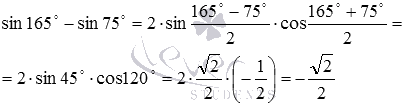
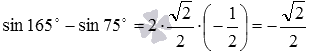
Формулы двойного аргумента для синуса и косинуса.
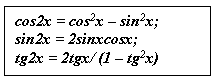
Формулы “синус двойного аргумента”, “косинус двойного аргумента” справедливы для любых значений аргумента.
Формула “тангенс двойного аргумента” справедлива лишь для тех значений аргумента х, для которых определены tgx, tg2x, 1- tg2x≠0
Пример2.
Упростите выражение:
,
Решение.
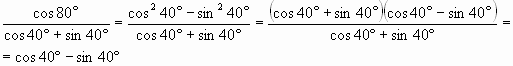
Ответ:
Задания к практической работе.
| Вариант 1 | Вариант 2 | |
| ||
| а) sin 105° + sin 75° | а) sin 105° — sin 75° | |
| б) cos π/12 - sin 7π/12 | б) sin 11π/12 + sin 5π/12 | |
| ||
| sin (π/3 + α ) + sin ( π/3 — α ) | sin (π/3 + α ) — sin ( π/3 — α ) | |
| ||
| а)1 + sin α = 2cos2 ( π/4 — α/2) б) 1 + sin2x = (cosx + sinx)2 в) cos2x = 1 – 2sin2x | а)1 — sin α = 2sin2 ( π/4 — α/2) б) 1 – sin2x = (cosx – sin)2 в) cos2x = 2cos2x – 1 | |
| ||
| | ||
| 1/2 + sin α . |  — 2 sin α — 2 sin α | |
| ||
| а) 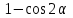 б) 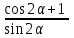 в) 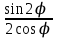 | а) 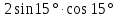 б) 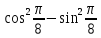 в) 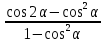 | |
Критерии оценки:
Оценка «5» ставится за 5 верно выполненных заданий
«4» - ставится за 4 верно выполненных задания «3» - за 3 верно выполненных задания
«2» - выполнено менее 3-х заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.