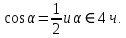Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx
Добавлен: 12.01.2024
Просмотров: 201
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 3.3. Основные тригонометрические тождества
Практическая работа № 16
Преобразования простейших тригонометрических выражений.
Цель: закрепление знаний, отработка навыков работы с формулами тригонометрии.
Пояснения к работе.
Пример 1. Преобразовать в произведение
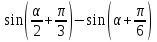
Решение. 2
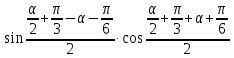 = 2
= 2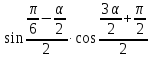 =2
=2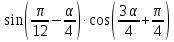
Пример 2.Упростите выражение:
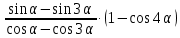 =
= 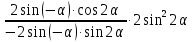 =-2
=-2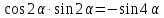
Пример 3.Упростите:
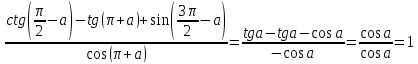
Задания к практической работе.
| Вариант 1 | Вариант 2 |
|
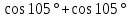 |
| 2. Вычислите: 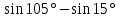 |
|
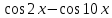 | произведение: 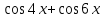 |
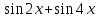 | произведение: 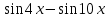 |
|
|
Если 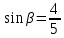 и и 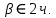 | 6.Найти: 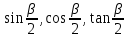 Если 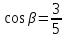 и и 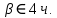 |
| 7.Найти 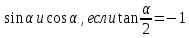 |
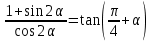 | тождество: 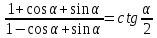 |
| 9. Вычислить: 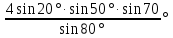 | 9. Вычислить: 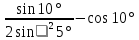 |
Критерии оценки:
«5»- ставится за 8 – 9 верно решенных задания;
«4» - ставится за 6 – 7 верно решенных задания;
«3» - ставится за 4 – 5 верно решенных задания;
«2» - выполнено менее 4 заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 3.4. Простейшие тригонометрические уравнения и неравенства
Практическая работа № 17
Решение тригонометрических уравнений
| Цель: способствовать закреплению навыков решения тригонометрических уравнений. Тригонометрическими уравнением называется равенство тригонометрических выражений, содержащее неизвестное (переменную) только под знаком тригонометрических функций. Решить тригонометрическое уравнение - значит найти все его корни - все значения переменной, удовлетворяющее уравнению. Решение тригонометрических уравнений сводятся к решению простейших тригонометрических уравнений, нахождение корней которых приведено в таблице:
| |
Задания к практической работе.
| Вариант 1. 1.Решите уравнения: а) sint =  б) cost = -  в) 2cos2t + 3cost +5=0 г) tg (2x + 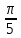 )= - )= -  2. Решите уравнения: а) 2 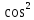 x = 1 + x = 1 +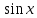 ; ;б) 2 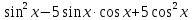 = 1 = 1 | Вариант 2. 1.Решите уравнения: а) sint = 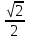 б) cost = - 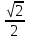 в) 2cos2t -5 cost + 2=0 г) ) tg (2x + 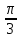 )= )=  2. Решите уравнение: а) 2 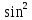 x = 1 - x = 1 - 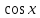 б) 5 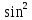 x - 5 x - 5 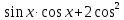 x = 1 x = 1 |
Критерии оценки:
«5» - ставится за 9-10 верно решенных уравнений;
«4» - ставится за 7-8 верно решенных уравнений;
«3» - ставится за 5-6 верно решенных уравнений;
«2» - если решено менее 5 уравнений.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 3.5. Простейшие тригонометрические уравнения и неравенства
Практическая работа № 18
Решение простейших тригонометрических уравнений и неравенств различными способами.
Цель: повторение изученного материала перед итоговой аттестацией.
Пояснения к работе.
1. Рассмотрите п. 9 с.67 учебника « Алгебра и начала анализа 10 – 11», примеры 1 – 9, разобранные в этом пункте.
2. Вспомните формулы решения простейших тригонометрических уравнений.
Задания к практической работе.
| Вариант 1. 1. Решите уравнения: а) 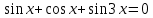 ; ;б) 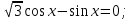 в) 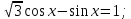 г) 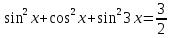 2. Решите неравенство: 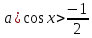 ; ; б) 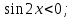 в) tg 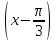 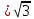 . .3. При каких значениях а уравнение  x – x – 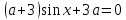 не имеет решений? не имеет решений?4 .Решите уравнение 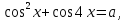 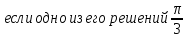 . . | Вариант 2. 1. Решите уравнение: а) 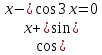 ; ; б) 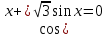 ; ;в) 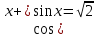 ; ;г) 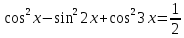 2. Решите неравенство: а) 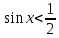 ; ;б) 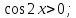 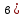 ctg ctg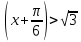 3. При каких значениях bуравнение 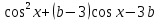 = 0 не имеет решений? = 0 не имеет решений?4. Решите уравнение 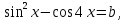 если одно из его решений если одно из его решений  . . |
 Критерии оценки:
Критерии оценки:«5» -ставится за все верно выполненные задания;
«4» - за 1 и 2, 1 и 3, 1 и 4 верно выполненные задания;
«3» - за 1 или за 2,3,4 верно выполненные задания;
«2» - во всех остальных случаях.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Раздел 4. Функции и графики.
Тема 4.1. Свойства функции.
Практическая работа № 19
Решение задач методом интервалов
Цель: способствовать закреплению навыков решения задач методом интервалов.
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 5 шагов:
-
Решить уравнение f (x) = 0. -
Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов. -
Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней. -
Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. -
Выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имеет вид f (x) > 0, или знаком «−», если неравенство имеет вид
f (x) < 0.
. Задания к практической работе.
| № | Вариант 1 | Вариант 2 |
| 1. | 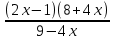 ≥ 0 ≥ 0 | 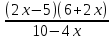 ≥ 0 ≥ 0 |
| 2. | 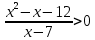 | 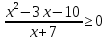 |
| 3. | 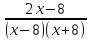  0 0 | 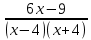  0 0 |
| 4. | Найти область определения функции: у = 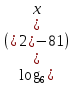 | Найти область определения функции: у =  1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 |
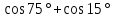
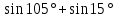
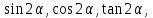 если
если