Файл: Крюков В.Г. Основы работоспособности технических систем.doc

Рассмотрим следующую СМО с простейшими потоками заявок λ и обслуживанияμ: поступившая заявка может обслуживаться любым свободным каналом; если всепканалов заняты, поступившая заявка становится в очередь и ждет своего обслуживания. Будем считать, что число мест в очереди неограниченно, причем более ранняя заявка, будет обслуживаться раньше.

Подобные системы называют СМО с ожиданием. Они характерны для крупных автоцентров и пунктов оплаты на платных дорогах. В этих системах общее число заявок, находящихся в системе, складывается из обслуживаемых заявок и заявок, находящихся в очереди. Поэтому СМО с ожиданием можно характеризовать следующим бесконечным множеством состояний:

А₀ – все n каналов свободны, в системе нет заявок и нет очереди;

………………………………………………………

А_k – занято k<n каналов, обслуживается k заявок, очереди нет;

…

А_n – заняты все n каналов, обслуживается n заявок, очереди нет.

А_n₊₁ – заняты все n каналов, обслуживается n заявок, одна заявка находится в очереди.

…

А_n₊_r – заняты все n каналов, обслуживается n заявок, в очереди находится r заявок.

…

Граф возможных состояний СМО с ожиданием показан на Рис 5.3 .

Рис 5.3 Схема СМО с ожиданием (без ограничения очереди)

Стационарное состояние системы описывается бесконечной системой алгебраических уравнений относительно вероятностей Р_kи_Pn₊_r. Эта система формируется по графу состояний в соответствии с ранее описанным мнемоническим правилом. Система имеет следующий вид:

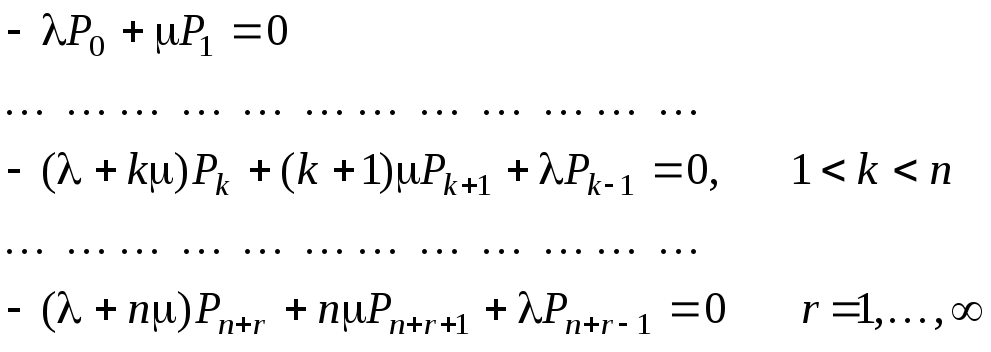(5.17)

при нормировочном условии .

Первые nуравнений системы (5.17) совпадают сn уравнениями для СМО с отказами и поэтому имеют решение в виде формул Эрланга:

;; (5.18)

Последние уравнения системы (5.17), начиная с п+1, одинаковы по структуре. С помощью вспомогательных переменных

(5.19)

эти уравнения можно записать в виде:

(5.20)

откуда имеем:

(5.21)

Учитывая соотношения (5.19) и (5.21), получим следующую рекуррентную формулу:

(5.22)

Применяя (5.22) последовательно rраз, получим:

(5.23)

Вероятность P₀можно найти из нормировочного условия, в которое подставим формулы (5.18) при0 ≤ k ≤ nи (5.23) приr ≥ 0:

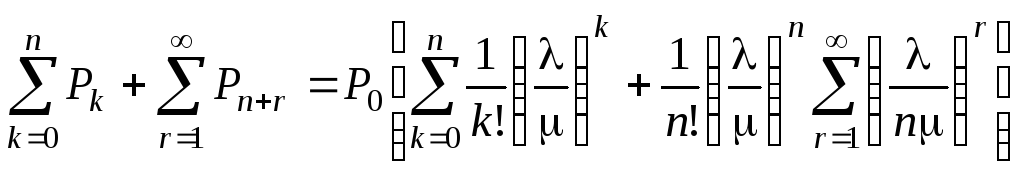(5.24)

Обозначим . Пусть, тогда сумма бесконечно убывающей геометрической прогрессии со знаменателемρравна. Соотношение (5.24) примет вид:

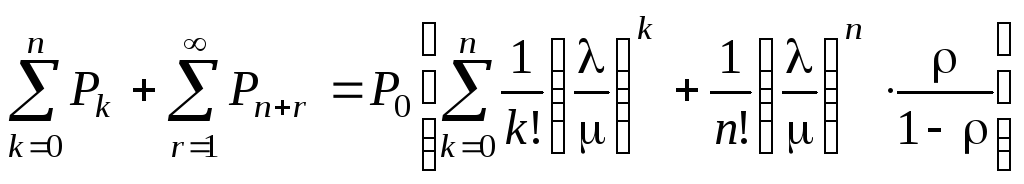(5.25)

Откуда:

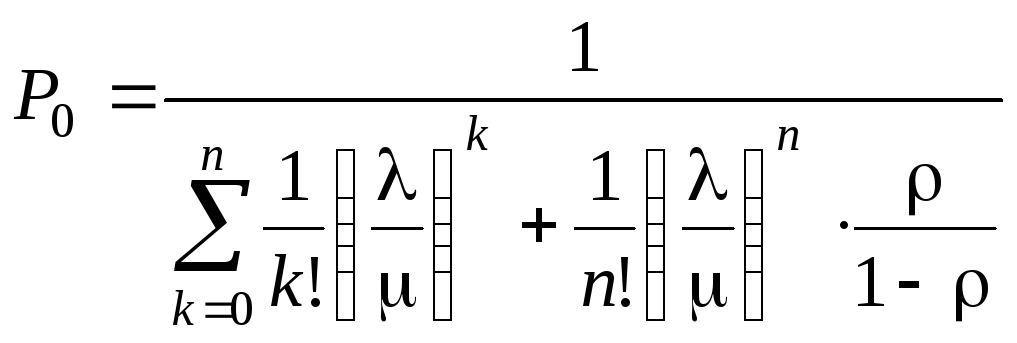(5.26)

С использованием соотношения (5.25) нетрудно подсчитать основные характеристики СМО с ожиданием в стационарном режиме, которые описываются следующими формулами:

- вероятность того, что все каналы свободны:

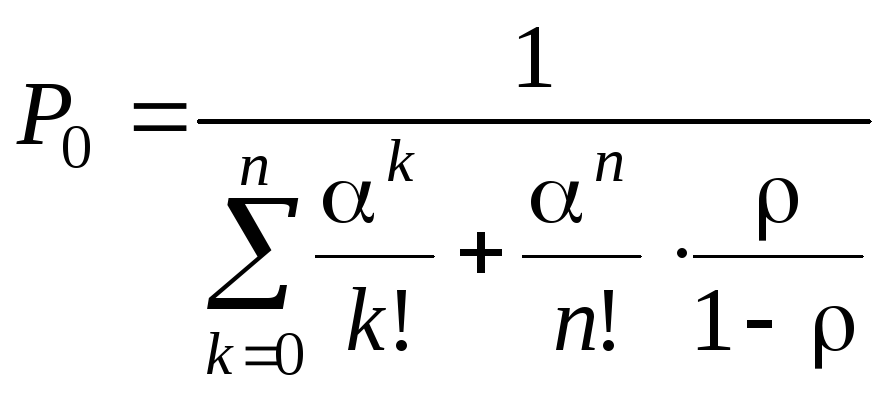(5.27)

- вероятность того, что все каналы заняты:

(28)

- вероятность того, что все n каналов заняты и r заявок находятся в очереди:

(5.29)

- среднее число заявок в очереди:

(5.30)

- среднее время ожидания заявок в очереди:

(5.31)

- среднее число каналов, свободных от обслуживания:

(5.32)

- среднее число каналов, занятых обслуживанием:

(5.33)

- коэффициент простоя каналов и коэффициент загрузки каналов:.

Параметр λ, как правило, определяется на основе статистических данных и подсчитывается в основном по количеству заявок, поступающих в систему в различные календарные сроки. Значение этого параметра имеет тенденцию возрастать в весеннее время и убывать зимой. Параметр μ определяется техническим оснащением и квалификацией обслуживающего персонала.

Контрольные вопросы

1. Какие типы станций существуют для технического обслуживания автомобилей?

2. Что такое система массового обслуживания? Приведите примеры.

3. Что такое поток заявок и поток обслуживания? Дайте математическое определение простейших потоков.

4. Раскройте смысл пуассоновского параметра λ в потоке заявок.

5. Раскройте смысл параметра μ в потоке обслуживания.

6. Дайте характеристику системе массового обслуживания с отказами.

7. Опишите мнемоническое правило для составления уравнения стационарного режима СМО с отказами.

8. На основе системы (5.6) получите формулу (5.9).

9. Для получения какого соотношения используется уравнение (5.7)?

10. В формуле (5.11) охарактеризуйте смысл каждого символа и индекса.

11. Как получается формула для вероятности отказа в обслуживании?

12. Вывести формулы (5.13) и (5.14).

13. Вывести формулы (5.15) и (5.16).

14. Станция технического обслуживания имеет 4 поста. В среднем в течение часа на станцию для обслуживания прибывает 4 автомобиля, среднее время обслуживания одного автомобиля на одном посту составляет 40 минут. Если все посты заняты, автомобили уезжают искать новую СТО. Найдите среднее число занятых каналов и вероятность того, что все каналы заняты?

15. Диспетчерская автовокзала предусматривает работу 2-х операторов, каждый оператор обслуживает в среднем 1-го клиента за 1 минуту. В среднем за одну минуту поступает 1,3 заявок. Диспетчерская работает в режиме СМО с отказом. Найти значения :

- если одновременно работают 2 диспетчера;

- если работает только 1 диспетчер.

16. Небольшое кафе имеет 6 индивидуальных столиков для обслуживания. В дневное время в среднем заходят 30 посетителей в час, среднее время нахождения в кафе каждого посетителя 15 минут. Если все столики заняты, посетители уходят не обслуженными. Найти значение и вероятность того, что число клиентов, находящихся одновременно в кафе будет не более 4-х? Найти среднее число обслуженных посетителей за 1 час? Если поставить еще один столик, на сколько в течение часа увеличится число обслуженных посетителей?

17. Найти вероятность того, что в условиях задачи 16 в кафе в течение часа зайдут 60 посетителей, а также вероятность того, что за 1 час за одним столиком будет обслужено 6 посетителей?

18. Базируясь на уравнениях (5.17) получить формулы(5.22) и (5.23)?

19. Доказать соотношение (5.26)?

20. Обосновать формулы (5.28) и (5.29)?

21. Доказать формулу (5.30)?

22. Доказать соотношения (5.31) и (5.32)?

23. В порту имеется 6 причалов. Среднее время разгрузки судна на одном причале составляет 0,7 суток. Ежедневно в порт прибывает в среднем 8 судов. Считая поток судов пуассоновским, найти:

- вероятность того, что за сутки прибудут 12 судов?

- вероятность того, что все причалы будут свободными?

- среднее за сутки число обслуженных судов?

- вероятность того, что все причалы будут заняты?

- среднее время ожидания в очереди?

- среднее число ожидающих судов?

24. На пропускном пункте платной автомобильной дороги имеется 6 постов оплаты. Один пост может обслуживать в час в среднем 60 автомобилей. В среднем по этой дороге в час проезжает 240 автомобилей, плата с 1-го автомобиля - 30 рублей. Найти:

- вероятность того, что в течение часа по дороге проедет 400 автомобилей?

- среднюю денежную выручку в час?

- среднее время ожидания автомобиля в очереди?

- вероятность того, что все посты заняты?

- при какой средней интенсивности движения очередь на пункты оплаты начнет неуклонно расти?