Файл: Крюков В.Г. Основы работоспособности технических систем.doc

(3.12)

распределенной нормально с параметрами, соответственно, математического ожидания M{X} = 0 и среднего квадратичного отклонения S{X} = 1 при плотности распределения:

(3.13)

Выражение (3.13) описывает плотность так называемого нормированного нормального распределения. Функция распределения случайной величины X запишется:

(3.14)

а из симметрии кривой f(x) следует, что f(-x) = f(x), откуда F(-x) = 1 - F(x) . В справочной литературе приведены расчетные значения функций f(x) и F(x) для различных x = (t - Т₀)/S, а также функции Лапласа:

(3.15)

Тогда показатели безотказности объекта для случайной величины T определяются через табличные значения f(x) и F(x) по выражениям:

f(t) = f(x)/S; Q(t) = F(x); (3.16)

P(t) = 1 - F(x); (3.17)

Чаще всего при оценке надежности объекта приходится решать прямую задачу, когда при заданных параметрах Т₀ и S нормально распределенной наработки до отказа определяется тот или иной показатель безотказности (например, ВБР) к интересующему значению наработки t. Но в ходе проектных работ приходится решать и обратную задачу – определение наработки, требуемой по техническому заданию, ВБР объекта. Для решения подобных задач используют квантили нормированного нормального распределения, где квантиль – это значение случайной величины, соответствующее заданной вероятности. Обозначим:

t_p– значение наработки, соответствующее вероятности безотказной работы P;

x_p – значение случайной величины X, соответствующее вероятности P.

Тогда из уравнения связи (3.12) x и t при x = x_p ; t = t_p, получаем:

t_p= Т₀ + x_p S (3.18)

Значения квантилей x_p приводятся в справочной литературе для P ≥ 0,5. При заданной вероятности P < 0,5 используется соотношение x_p = - x_1-p . Например, при P = 0,3 имеем: x_0,3 = - x_{1- 0,3} = - x_{0, 7}.

Вероятность попадания случайной величины наработки T в заданный интервал [t₁, t₂] наработки определяется:

(3.19)

где x₁ = (t₁ - Т₀)/S, x₂ = (t₂ - Т₀)/S .

Отметим, что наработка до отказа всегда положительна, а кривая f(t), в общем случае, начинается от t = - ∞ и распространяется до t = ∞. Это не является существенным недостатком, если Т₀ >> S, поскольку по (3.19) нетрудно подсчитать, что вероятность попадания случайной величины T в интервал P{Т₀ - 3S < T < Т₀ + 3S} ≈ 1,0 с точностью до 1%. А это означает, что все возможные значения (с погрешностью не выше 1%) нормально распределенной случайной величины с соотношением характеристик Т₀ > 3S, находятся на участке Т₀ ± 3S.

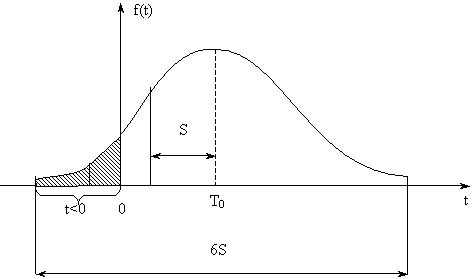
Рис. 3.7 Усеченное нормальное распределение

При большем разбросе значений случайной величины T область возможных значений ограничивается слева (0, ∞) и тогда используется усеченное нормальное распределение. Оно применяется из-за того, что при малых значениях Т₀ и большом S, может возникать ситуация, когда f(t) «покрывает» своей левой ветвью область отрицательных наработок (Рис. 3.7).

Усеченным нормальным распределением называется распределение, получаемое из классического нормального, при ограничении интервала возможных значений наработки до отказа. В общем случае усечение может быть: левым – (0; ∞) или двусторонним – (t₁, t₂).

Рассмотрим усеченное нормальное распределение (УНР) для случая ограничения случайной величины наработки интервалом (t₁, t₂).

Плотность УНР определяется по формуле , гдеf(t) вычисляется по соотношению (3.11), а c – нормирующий множитель, определяемый из условия, что площадь под кривой равна 1, т. е.:

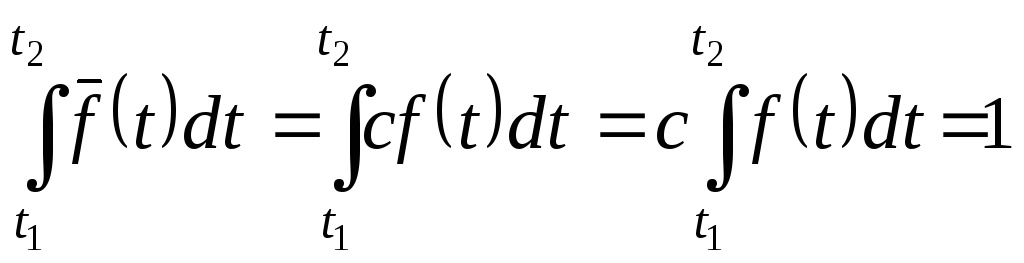(3.20)

откуда получаем: .

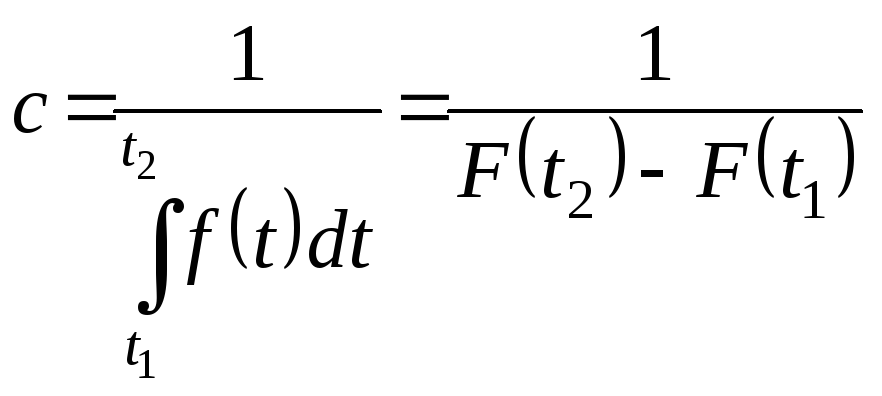Применяя переход от случайной величины Т = {t} к величине X = {x}: x₂ = (t₂ – Т₀)/S ; x₁ = (t₁ – Т₀)/S, легко находим, что .

К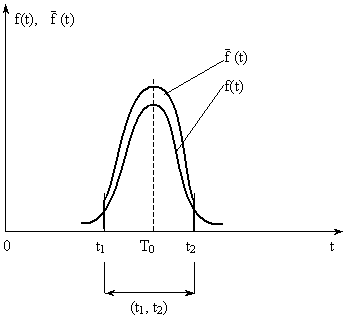риваявыше, чемf(t), т. к. площади под кривымииf(t)одинаковы и равны 1 (Рис. 3.8).

Рис. 3.8 Сравнение усеченного нормального и нормального распределений

Показатели безотказности для УНР в диапазоне (t₁ , t₂) определяются по формулам:

(3.21)

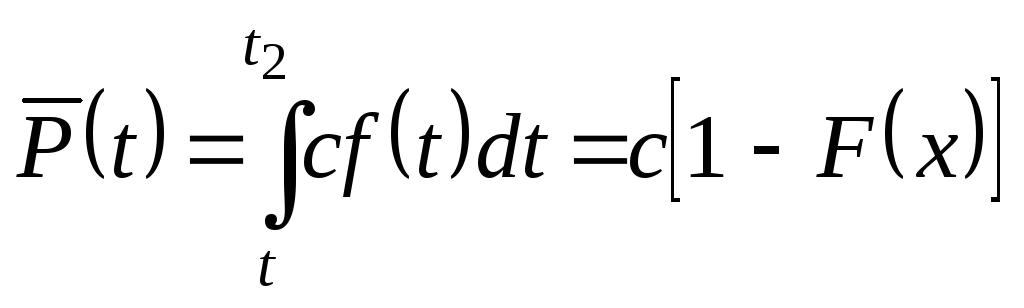(3.22)

(3.23)

(3.24)

УНР для положительной наработки до отказа, т.е. в диапазоне (0; ∞) имеет плотность распределения отказов , гдеc₀ - нормирующий множитель определяется из условия: . И далее используются формулы (3.21-3.24), в которые вместос подставляется с₀.

3.3 Законы распределения наработки до отказа

Экспоненциальное распределение.

Экспоненциальное распределение описывает наработку до отказа объектов, у которых в результате сдаточных испытаний (выходного контроля) отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации. Эти объекты можно отнести к «нестареющим», поскольку они работают только на участке с λ(t) = λ = const. Круг таких объектов широк: сложные технические системы с множеством компонентов, средства вычислительной техники и системы автоматического регулирования и т. п. Экспоненциальное распределение широко применяется для оценки надежности энергетических объектов.

Считается, что случайная величина наработки объекта до отказа подчинена экспоненциальному распределению, если ПРО описывается выражением:

f(t) = α exp( -αt), (3.25)

где α – параметр распределения, который по результатам испытаний принимается равным , где– оценка средней наработки до отказа. Остальные показатели безотказности при известнойf(t), определяются по формулам:

- вероятность безотказной работы (ВБР): P(t) = exp ( - αt), (3.26)

- вероятность отказа (ВО): Q(t) = 1 - exp ( - αt), (3.27)

- интенсивность отказов (ИО): λ(t) = α exp ( -αt) / exp ( - αt) = α (3.28)

Из (3.28) следует, что ИО является постоянной величиной, не зависящей от времени, и обратно пропорциональной оценке средней наработки .

Числовые характеристики наработки до отказа определяются по формулам:

- средняя наработка (МО наработки) до отказа

(3.29)

- дисперсия наработки до отказа

(3.30)

Рассмотренные далее законы распределения наработки до отказа используются на практике для описания надежности «стареющих» объектов, подверженных износовым отказам.

Логарифмически нормальное (логнормальное) распределение.

При логарифмически нормальном распределении нормально распределенным является логарифм () случайной величиныT, а не сама эта величина. Логарифмически нормальное распределение во многом более точно, чем нормальное описывает наработку до отказа тех объектов, у которых отказ возникает вследствие усталости, например, подшипников качения, электронных ламп и пр. Если величина имеет нормальное распределение с параметрами: математическое ожиданиеU и среднеквадратичное отклонение V, то величина T считается логарифмически нормально распределенной с ПРО, описываемой:

(3.31)

Параметры U и V по результатам испытаний принимаются:

(3.32)

(3.33)

где и- статистические оценки параметровU и V.

Показатели надежности можно рассчитать по вышеприведенным выражениям, пользуясь табулированными функциями f(x) и, соответственно, F(x) и Φ(x) для нормального распределения при . Графики изменения показателей надежности при логарифмически нормальном распределении приведены на Рис. 3.9. Числовые характеристики наработки до отказа:

- средняя наработка (МО наработки) до отказа

(3.34)

Рис. 3.9 Показатели надежности при логарифмически нормальном распределении

- дисперсия наработки до отказа

(3.35)

Гамма–распределение.

Случайная величина наработки до отказа T имеет гамма-распределение с параметрами α (масштабный параметр) и β (параметр формы), где α, β > 0, причем β – целое число, если ее ПРО описывается выражением: