Файл: Крюков В.Г. Основы работоспособности технических систем.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.10.2024
Просмотров: 364
Скачиваний: 0
СОДЕРЖАНИЕ
Кафедра Автомобильных Двигателей и Сервиса
Тема 1. Технические системы: качество, работоспособность, диагностика
1.1 Техническая система и ее жизненный цикл
1.2 Качество и работоспособность технических систем.
Понятие о техническом состоянии автомобиля.
Причины и последствия изменения технического состояния
1.3 Работоспособность и диагностика технической системы
Оценка работоспособности технической системы.
Рис 1.4 Прямые и косвенные методы определения рабочих параметров Свойства диагностических параметров
Тема 2 показатели и характеристики надежности
2.1 Основные понятия надежности. Классификация отказов Основные понятия
Классификация и характеристики отказов
2.2 Количественные показатели безотказности
2.3 Связи показателей надежности. Характеристики безотказности
3.1 Общие понятия. Статистическая обработка испытаний
3.2 Нормальный закон распределения наработки до отказа Классическое нормальное распределение.
3.3 Законы распределения наработки до отказа
3.4 Надежность систем. Общие понятия и определения
Рис 3.13 Примеры ненагруженного резервирования
3.5 Надежность основной системы
Тема 4. Сбор информации и идентификация моделей
4.1. Методы сбора информации о надежности автомобиля.
4.2. Идентификация работы двигателя по результатам стендовых испытаний:
4.3 Моделирование работы двигателя в эксплуатации
Тема 5 производительность средств обслуживания
5.1. Предприятия технического обслуживания и смо
5.2 Системы массового обслуживания с отказами
5.3 Система массового обслуживания с ожиданием
Тема 6. Управление станциями технического обслуживания автомобилей
![]() (2.10)
(2.10)
ПРО по существу является плотностью распределения (плотностью вероятности) случайной величины T наработки объекта до отказа. Поскольку Q(t) является неубывающей функцией своего аргумента, то f(t) ≥ 0. Один из возможных видов графика f(t) приведен на Рис. 2.3.
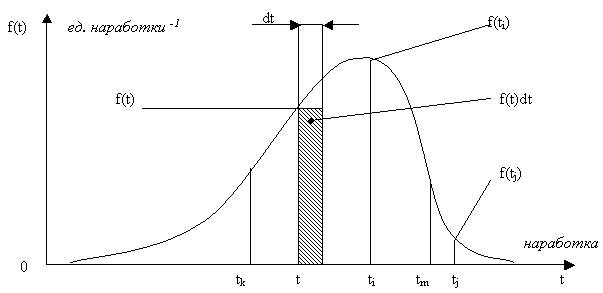
Рис. 2.3 Плотность распределения отказов в зависимости от наработки
Вероятность того, что отказ случится в интервале [t, t + dt] равна:
![]() (2.11)
(2.11)
где f(t)dt – элемент ВО объекта в интервале [t, t + dt] (геометрически это площадь заштрихованного прямоугольника, опирающегося на отрезок dt).
Отсюда:
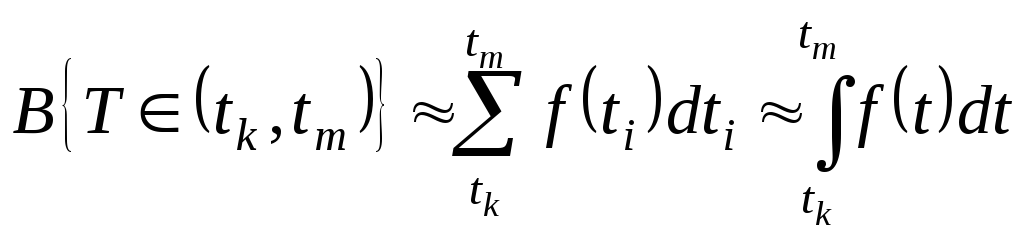 (2.12)
(2.12)
что геометрически интерпретируется площадью под кривой f(t), опирающейся на участок [tk, tm]. ВО и ВБР можно выразить в функции ПРО.
Поскольку Q(t) = B{T < t}, то используя выражение (2.12), получим:
![]() (2.13)
(2.13)
расширение интервала слева до нуля вызвано тем, что T не может быть отрицательной.
Т. к. P(t) = B{T ≥ t}, то
![]() (2.14)
(2.14)
Очевидно, что Q(t) представляет собой площадь под кривой f(t) слева от t, а P(t) – площадь под f(t) справа от t. Поскольку все, полученные при испытаниях значения наработок лежат под кривой f(t), то
![]() (2.15)
(2.15)
Интенсивность отказов (ИО)
Статистическая оценка ИО определяется
![]() (2.16)
(2.16)
отношением числа объектов ∆n(t, t + ∆t), отказавших в интервале наработки [t, t + ∆t] к произведению числа N(t) работоспособных объектов в момент t на длительность интервала наработки ∆t. Сравнивая (2.8) и (2.16) можно отметить, что ИО несколько полнее характеризует надежность объекта на момент наработки t, т. к. показывает частоту отказов, отнесенную к фактически работоспособному числу объектов на момент наработки t. Вероятностное определение ИО получим, умножив и поделив правую часть выражения (2.16) на N
![]() (2.17)
(2.17)
С
учетом (2.9),оценку ИО
![]() можно представить:
можно представить:
![]() (2.18)
(2.18)
откуда при стремлении ∆t → 0 и N → ∞ получаем
![]() (2.19)
(2.19)
2.3 Связи показателей надежности. Характеристики безотказности
Уравнение связи показателей надежности
Поскольку интенсивность отказов λ(t) является более полной характеристикой надежности, представляет интерес выразить P(t) через λ(t). Используя выражение для интенсивности отказов
![]() (2.20)
(2.20)
запишем
dP(t) /dt = - λ(t)·P(t) (2.21)
Разделяя переменные, интегрируя от 0 до t и принимая во внимание, что при t = 0 вероятность безотказной работы объекта P(0) = 1, получаем
![]() (2.22)
(2.22)
откуда уравнение связи основных показателей надежности имеет вид:
![]() (2.23)
(2.23)
Величина λ(t) dt – есть вероятность того, что элемент, безотказно проработавший в интервале наработки [0, t], откажет в интервале [t, t + dt].Уравнение связи показывает, что все показатели надежности P(t), Q(t), f(t) и λ(t) равноправны в том смысле, что зная один из них, можно определить другие.
Числовые характеристики безотказности невосстанавливаемых объектов
Средняя наработка до отказа Рассмотренные выше функциональные показатели надежности P(t), Q(t), f(t) и λ(t) полностью описывают случайную величину наработки T = {t}. В то же время для решения ряда практических задач надежности бывает достаточно знать некоторые числовые характеристики этой случайной величины и, в первую очередь, среднюю наработку до отказа, которая может быть статистической или вероятностной.
Статистическая оценка средней наработки до отказа определяется по формуле:
![]() (2.24)
(2.24)
где ti – наработка до отказа i-го объекта.
При вероятностном определении средняя наработка до отказа представляет собой математическое ожидание случайной величины T и определяется:
![]() (2.25)
(2.25)
Используя
выражение для плотности распределения
отказов![]() и
интегрируя
по частям, можно преобразовать (2.25) к
виду
и
интегрируя
по частям, можно преобразовать (2.25) к
виду
![]() (2.26)
(2.26)
с учетом того, что P(0) = 1, P(∞) = 0.
Из (7) следует, что средняя наработка до отказа геометрически интерпретируется как площадь под кривой P(t) (Рис. 2.4). Математическое ожидание (МО) наработки T0 означает математически ожидаемую наработку до отказа однотипных элементов, т. е. усредненную наработку до первого отказа
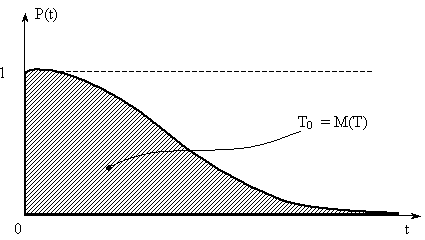
Рис. 2.4 Изменение P(t) в зависимости от наработки
Очевидно,
что с увеличением выборки испытаний N
→ ∞ средняя
арифметическая наработка (оценка![]() )
сходится кТ0
.На
практике также представляют интерес
условные
средние наработки:
)
сходится кТ0
.На
практике также представляют интерес
условные
средние наработки:
-
средняя
полезная наработка
![]() определенная при условии, что при
достижении наработки t1
все оставшиеся работоспособными объекты
снимаются с эксплуатации;
определенная при условии, что при
достижении наработки t1
все оставшиеся работоспособными объекты
снимаются с эксплуатации;
средняя продолжительность предстоящей работы
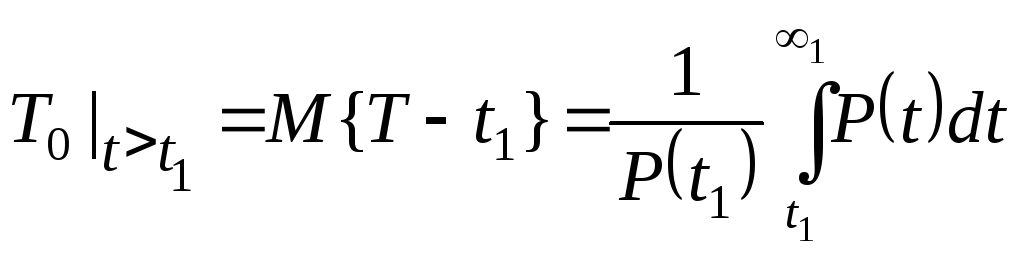 (2.27)
(2.27)
при условии, что объект безотказно работал на интервале (0, t1).
Причины использования этих показателей:
1. Высоконадежные объекты (элементы электронных схем), как правило, эксплуатируются меньший срок чем T0 (tэкс < T0), т. е. заменяются по причине морального старения раньше, чем успевают наработать T0.
2. Часто для указанных объектов сокращают период испытаний (проводят до наработок соответствующих их моральному старению), поэтому T0 в таком случае понимают как среднюю наработку, которая имела бы место в действительности, если бы λ(t) оставалась такой, какой она была в начальный период испытаний.
Величины
![]() ,
,![]() иT0:связаны
между собой по формуле:
иT0:связаны
между собой по формуле:
![]() Понятия
Понятия![]() и
и![]() иллюстрируются на Рис. 2.5.
иллюстрируются на Рис. 2.5.
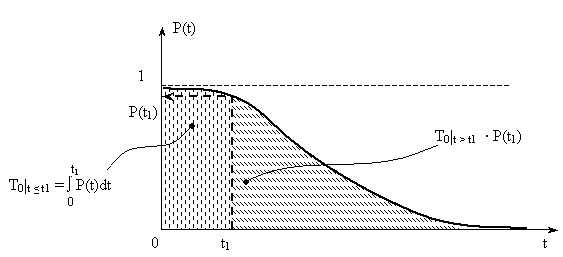
Рис.
2.5 Связь величин
![]() и
и![]()
В
то же время средняя наработка не может
полностью характеризовать безотказность
объекта. Так при равных средних наработках
до отказа T0
надежность объектов 1 и 2 может весьма
существенно различаться (Рис. 2.6).
Очевидно, что в виду большего рассеивания
наработки до отказа (кривая ПРО f2(t)
ниже и шире), объект 2 менее надежен, чем
объект 1.Поэтому для оценки надежности
объекта по величине
![]() необходимо еще знать и показатель
рассеивания случайной величиныT
= {t}, около
средней наработки T0.
К числу показателей рассеивания относятся
дисперсия
и среднее
квадратичное отклонение
(СКО) наработки до отказа.
необходимо еще знать и показатель
рассеивания случайной величиныT
= {t}, около
средней наработки T0.
К числу показателей рассеивания относятся
дисперсия
и среднее
квадратичное отклонение
(СКО) наработки до отказа.
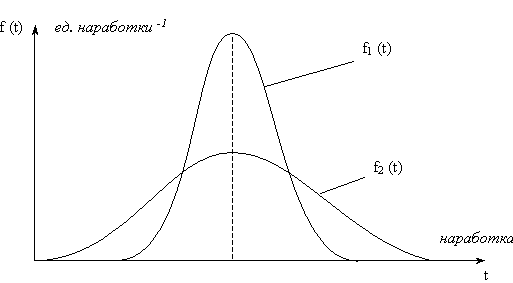
Рис. 2.6 Кривые ПРО f1(t) и f2(t) при различных значениях дисперсии
Дисперсия случайной величины наработки:
- статистическая оценка
![]() (2.28)
(2.28)
- вероятностное определение
![]() (2.29)
(2.29)
СКО случайной величины наработки:
![]() или
или![]() (2.30)
(2.30)
Средняя наработка до отказа T0 и СКО наработки S имеют размерность [ед. наработки-1], а дисперсия D - [ед. наработки -2].
Контрольные вопросы:
1. В чем заключается понятие надежности как свойства объекта?
2. Перечислите и дайте определения основных состояний и событий, которыми характеризуется надежность?
3. При каких условиях наступает предельное состояние объекта?
4. Какими могут быть объекты по способности к восстановлению работоспособного состояния?