Файл: Крюков В.Г. Основы работоспособности технических систем.doc

- дорожные: (1, 2 рабочих поста), которые предназначены для устранения мелких неисправностей, возникающих в пути. Часто такие станции сооружаются вместе с заправками. Кроме того, к дорожным станциям технического обслуживания следует отнести передвижные рабочие посты, предназначенные для устранения неисправностей транспортных средств.

Системы массового обслуживания. Основные понятия

Предположим, что имеется набор последовательно возникающих заявок, выполнение каждой из которых есть некое действие, осуществляемое специальным устройством - узлом обслуживания. Например, узел обслуживания - это железнодорожная касса, в которую в качестве «заявок на обслуживание» заходят пассажиры за билетами.(Рис. 5.1)

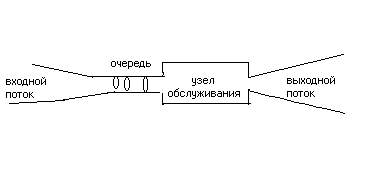
Рис 5.1 Простейшая схема для СМО с одним узлом обслуживания

Это - ситуация системы массового обслуживания (СМО), которая имеет две особенности:

- заявки приходят на обслуживание хаотично, в случайные моменты времени;

- время, в течение которого заявка находится в СМО (в очереди и в узле обслуживания) является также случайной величиной.

В промышленности, в сельском хозяйстве, в сфере услуг можно встретить большое разнообразие систем массового обслуживания. Для их описания и моделирования была создана научно-практическая дисциплина «Теория СМО».Некоторые фрагменты этой дисциплины рассмотрены ниже. В частности, будем рассматривать простейшие потоки заявок и обслуживания. Простейшие потоки обладают следующими свойствами:

- стационарность означает, что среднее число заявок за единицу времени и закономерность поступления заявок зависит лишь от длительности интервала и не зависит от сдвига этого интервала по оси времени;

- ординарность означает, что в определенный момент времени в систему не могут поступить 2 заявки одновременно.

Для простейших потоков промежуток времени между последовательно поступающими заявками (будучи величиной случайной) имеет следующую функцию распределения:

(5.1)

при некотором и соответствующий поток заявок называетсяпуассоновским.

Время, в течение которого очередная заявка в СМО находится на обслуживании, также является величиной случайной. Если функция распределения этой случайной величины имеет вид:

(5.2)

при некотором , то время обслуживания называетсяэкспоненциальным.

В пуассоновском потоке заявок при любом режиме обслуживания вероятность поступления k заявок за время t равна:

. (5.3)

Для этого потока заявок имеется полное описание ряда случайной величины, которая представляет собой число заявок, поступивших за время t. Это позволяет подсчитать ее математическое ожидание:

(5.4)

Это значит, что . Следовательно, смысл пуассоновского параметраλ в том, что это есть среднее число заявок, поступающих в единицу времени. Можно провести аналогичные рассуждения в связи с экспоненциальным временем обслуживания. А именно, если является функцией распределения времени обслуживания (при неотрицательных значенияхt, а при отрицательных она равна нулю), то математическое ожидание времени обслуживания есть величина:

. (5.5)

Следовательно, среднее время обслуживания одной заявки равно , поэтому в единицу времени (при экспоненциальном обслуживании) в среднем обслуживаетсязаявок. Обычно реальные СМО имеют несколько каналов обслуживания и правила обслуживания могут быть различными. Ниже рассмотрим математические модели 2-х типов: СМО с отказами и СМО с ожиданием

5.2 Системы массового обслуживания с отказами

Этот тип СМО характерен для дорожных или небольших станций технического обслуживания. Допустим, что в этой СМО имеется nравнодоступных постов обслуживания и действуют два потока:

- входной поток заявок;

- поток освобождения постов (каналов).

Пусть оба потока являются простейшими с интенсивностью соответственно λиμ.

СМО с отказами характерна тем, что если заявка застает свободным хотя бы один канал, то она принимается к обслуживанию и обслуживается до конца любым из свободных каналов. Если же заявка застает все nканалов занятыми, то она получает отказ и покидает систему не обслуженной.

СМО с отказами описывается следующим множеством состояний:

А₀– всеnканалов свободны, в системе нет заявок;

А₁– занят один канал, обслуживается 1 заявка;

………………………………………………………

А_k– занятоk<nканалов, обслуживаетсяkзаявок;

………………………………………………………

А_n– заняты всеnканалов, обслуживаетсяnзаявок.

Размеченный граф состояний для СМО с отказами может быть представлен в виде приведенным на Рис. 5.2:

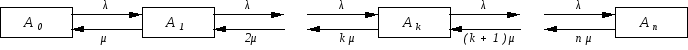
Рис. 5.2 Схема СМО с отказами

Рассмотрим стационарное состояние системы. Поскольку все потоки, действующие в системе, являются простейшими, в системе протекает марковскийпроцесс. В этом случае для вывода уравнений процесса можно воспользоваться следующим мнемоническим правилом: алгебраическая сумма слагаемых, каждое из которых представляет собой произведение вероятностиP_kнахождения системы в каком-либо определенномk-ом состоянии на интенсивность потока, переводящего систему в другое состояние, равна нулю. Число слагаемых равно сумме стрелок, входящих и выходящих из состоянияA_k, причем для входящих стрелок соответствующее слагаемое берется со знаком плюс, а для выходящих – со знаком минус.

Система алгебраических уравнений, описывающая стационарный режим работы СМО и составленная по графу возможных состояний в соответствии с мнемоническим правилом, имеет следующий вид:

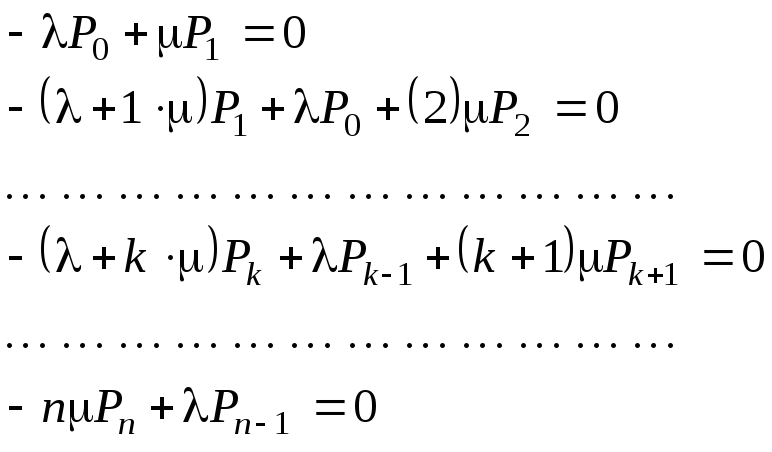k = 1, …, (n - 1) (5.6)

К данной системе добавляется очевидное нормировочное условие для вероятностей нахождения СМО в определенных состояниях:

(5.7)

Для решения системы (5.6) введем вспомогательные переменныеи запишем систему (5.6) в следующем виде:

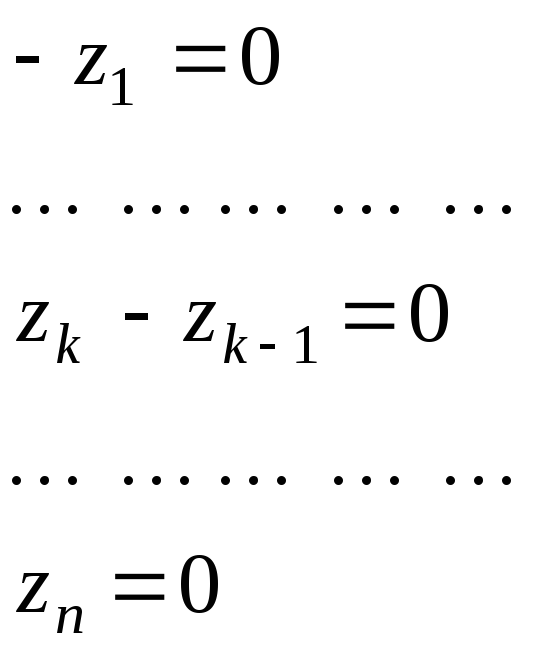k = 1, …, (n - 1) (5.8)

Однородная система алгебраических уравнений (5.8) имеет нулевое решение , из которого можно получить следующую рекуррентную формулу:, k = 1, …, n. Отсюда:

k = 1, …, n (5.9)

Используя нормировочное условие (5.7) можно найти, что:

(5.10)

Подставив (5.10) в (5.9), получим основные расчетные формулы для вероятностей нахождения системы в определенном k-ом состоянии (формулы Эрланга):

k = 0, …, n (5.11)

Формулы Эрланга (5.11) дают предельный закон распределения вероятностей числа занятых каналов в зависимости от параметров входного потока заявок и потока обслуживания. Поведение СМО с отказами в стационарном режиме описывается следующими основными характеристиками:

Вероятность отказа заявке в обслуживании:

(5.12)

Вероятность того, что поступившая заявка будет принята к обслуживанию:

(5.13)

Среднее число занятых каналов:

(5.14)

Вероятность того, что занят любой канал:

Среднее время простоя канала:

(5.15)

Среднее время полной загрузки системы:

(5.16)

Вероятности состояния системы массового обслуживания с отказами зависят от трех параметров: n, λ, μ. Поэтому выбор местоположения станции технического обслуживания и ее размеры должны быть такими, чтобы вероятность отказа была минимальной. Вероятность простоя станции также должна быть минимальной. Работа станции в основном зависит от параметра λ, который определяется количеством автомобилей в районе обслуживания станции и от параметра μ, который зависит от квалификации работников.