Файл: Крюков В.Г. Основы работоспособности технических систем.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.10.2024
Просмотров: 368
Скачиваний: 0
СОДЕРЖАНИЕ
Кафедра Автомобильных Двигателей и Сервиса
Тема 1. Технические системы: качество, работоспособность, диагностика
1.1 Техническая система и ее жизненный цикл
1.2 Качество и работоспособность технических систем.
Понятие о техническом состоянии автомобиля.
Причины и последствия изменения технического состояния
1.3 Работоспособность и диагностика технической системы
Оценка работоспособности технической системы.
Рис 1.4 Прямые и косвенные методы определения рабочих параметров Свойства диагностических параметров
Тема 2 показатели и характеристики надежности
2.1 Основные понятия надежности. Классификация отказов Основные понятия
Классификация и характеристики отказов
2.2 Количественные показатели безотказности
2.3 Связи показателей надежности. Характеристики безотказности
3.1 Общие понятия. Статистическая обработка испытаний
3.2 Нормальный закон распределения наработки до отказа Классическое нормальное распределение.
3.3 Законы распределения наработки до отказа
3.4 Надежность систем. Общие понятия и определения
Рис 3.13 Примеры ненагруженного резервирования
3.5 Надежность основной системы
Тема 4. Сбор информации и идентификация моделей
4.1. Методы сбора информации о надежности автомобиля.
4.2. Идентификация работы двигателя по результатам стендовых испытаний:
4.3 Моделирование работы двигателя в эксплуатации
Тема 5 производительность средств обслуживания
5.1. Предприятия технического обслуживания и смо
5.2 Системы массового обслуживания с отказами
5.3 Система массового обслуживания с ожиданием
Тема 6. Управление станциями технического обслуживания автомобилей
Составляющие надежности
Надежность является комплексным свойством, включающим в себя в зависимости от назначения объекта или условий его эксплуатации ряд простых свойств:
Безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторой наработки или в течение некоторого времени.
Наработка – продолжительность или объем работы объекта, измеряемая в любых неубывающих величинах (единица времени, число циклов нагружения, километры пробега и т. п.).
Долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонтов.
Ремонтопригодность – свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению причин возникновения отказов, поддержанию и восстановлению работоспособности путем проведения ремонтов и технического обслуживания.
Сохраняемость – свойство объекта непрерывно сохранять требуемые эксплуатационные показатели в течение (и после) срока хранения и транспортирования.
В зависимости от объекта надежность может определяться всеми перечисленными свойствами или частью их. Например, надежность колеса зубчатой передачи, подшипников определяется их долговечностью, а станка – долговечностью, безотказностью и ремонтопригодностью.
Показатели надежности количественно характеризуют, в какой степени данному объекту присущи определенные свойства, обусловливающие надежность. Одни показатели надежности (например, технический ресурс, срок службы) могут иметь размерность, ряд других (например, вероятность безотказной работы, коэффициент готовности) являются безразмерными.
Рассмотрим ,например ,показатели надежности обуславливающие- долговечность.
Технический ресурс – наработка объекта от начала его эксплуатации или возобновления эксплуатации после ремонта до наступления предельного состояния. Строго говоря, технический ресурс может быть регламентирован следующим образом: до среднего, капитального, от капитального до ближайшего среднего ремонта и т. п. Если регламентация отсутствует, то имеется в виду ресурс от начала эксплуатации до достижения предельного состояния после всех видов ремонтов. Для невосстанавливаемых объектов понятия технического ресурса и наработки до отказа совпадают.
Назначенный ресурс – суммарная наработка объекта, при достижении которой эксплуатация должна быть прекращена независимо от его состояния.
Срок службы – календарная продолжительность эксплуатации (в том числе, хранение, ремонт и т. п.) от ее начала до наступления предельного состояния.
На Рис.2.1 приведена графическая интерпретация перечисленных показателей, при этом:
t0 = 0 – начало эксплуатации t1, t5 – моменты отключения по технологическим причинам;
t2, t4 t6, t8 – моменты включения объекта;
t3, t7– моменты вывода объекта в ремонт, соответственно, средний и капитальный;
t9– момент прекращения эксплуатации; t10 – момент отказа объекта.
Р ис
2.1.Иллюстрация показателей надежности
ис
2.1.Иллюстрация показателей надежности
Технический ресурс (наработка до отказа)
ТР = t1+ (t3 – t2 ) + (t5 – t4) + (t7 – t6) + (t10 – t8).
Назначенный ресурс
ТН = t1 + (t3 –t2 ) + (t5 – t4 ) + (t7 –t6 ) + (t9 –t8 ).
Срок службы объекта ТС = t10 . Для большинства технических объектов в качестве критерия долговечности чаще всего используется технический ресурс.
2.2 Количественные показатели безотказности
Общие понятия
Наиболее важными показателями надежности невосстанавливаемых объектов являются показатели безотказности, к которым относятся:
- вероятность безотказной работы;
- плотность распределения отказов;
- интенсивность отказов;
- средняя наработка до отказа.
Показатели надежности представляются в двух формах (определениях):
- статистическая (выборочные оценки); Эта форма показателей получается по результатам ограниченного числа испытаний на надежность. Для обозначения статистических оценок будем использовать знак ^ (“шляпка”). Показатели, определенные для выборки, и, позволяющие сделать какие-то выводы о случайной величине, являются выборочными (статистическими) оценками
- вероятностная. Эта форма получается из общей «генеральной совокупности», имеющей неограниченный объем данных о наработке до отказа объекта Количественные показатели, определенные для «генеральной совокупности», являются истинными (вероятностными) показателями, поскольку объективно характеризуют случайную величину – наработку до отказа
Допустим, что в ходе испытаний какого-то числа однотипных объектов получено конечное число интересующего нас параметра – наработки до отказа. Полученные числа представляют собой статистическую выборку, которая при достаточно большом числе испытаний (большой выборке) приближается к вероятностной. Вероятностная форма представления показателей удобна при аналитических расчетах, а статистическая – при экспериментальном исследовании надежности. Обычно принимается следующая схема испытаний для оценки надежности:
Пусть на испытания поставлено N одинаковых серийных объектов. Условия испытаний идентичны, а испытания каждого из объектов проводятся до его отказа. Введем следующие обозначения:
T = {0, t1, … tN } = {t} – случайная величина наработки объекта до отказа;
N(t) – число объектов, работоспособных к моменту наработки t;
n(t) – число объектов, отказавших к моменту наработки t;
Δn(t, t + Δt) – число объектов, отказавших в интервале наработки [t, t + Δt];
Δt – длительность интервала наработки.
Вероятность безотказной работы (ВБР)
Статистическая оценка ВБР (эмпирическая функция надежности) определяется отношением числа N(t) объектов, безотказно проработавших до момента наработки t, к числу объектов, исправных к началу испытаний (t = 0) - к общему числу объектов N:
![]() (2.1)
(2.1)
Оценку ВБР можно рассматривать как показатель доли работоспособных объектов к моменту наработки t.
Поскольку N(t) = N - n(t), то ВБР по (2.1)
![]() (2.2)
(2.2)
где
![]() (t)
– оценка вероятности отказа (ВО).
(t)
– оценка вероятности отказа (ВО).
В статистическом определении оценка ВО представляет эмпирическую функцию распределения отказов. Так как события, заключающиеся в наступлении или не наступлении отказа к моменту наработки t, являются противоположными, то
![]() (2.3)
(2.3)
Нетрудно убедиться, что ВБР является убывающей, а ВО – возрастающей функцией наработки. Действительно
-
в момент начала испытаний t
= 0 число работоспособных объектов равно
общему их числу N(0)
= N, а число
отказавших - n(0)
= 0, поэтому
![]() ,
а
,
а![]() ;
;
-
при наработке t
→ ∞ все
объекты, поставленные на испытания,
откажут, т. е. N(∞)
= 0, а n(∞)
= N, поэтому
![]() ,
а
,
а![]() .
.
Вероятность безотказной работы определяется по соотношению:
P(t) = B{T ≥ t}. (2.4)
Таким образом, ВБР есть вероятность того, что случайная величина наработки до отказа T окажется не меньше некоторой заданной наработки t. Очевидно, что ВО будет являться функцией распределения случайной величины T и представляет из себя вероятность того, что наработка до отказа окажется меньше некоторой заданной наработки t:
Q(t) = B{T < t}. (2.5)
Графики
ВБР и ВО приведены на Рис. 2.2.
В пределе, с ростом числа N
(увеличение выборки)
испытываемых
объектов,
![]() и
и![]() сходятся по вероятности (приближаются
по значениям) кP(t)
и Q(t).
сходятся по вероятности (приближаются
по значениям) кP(t)
и Q(t).
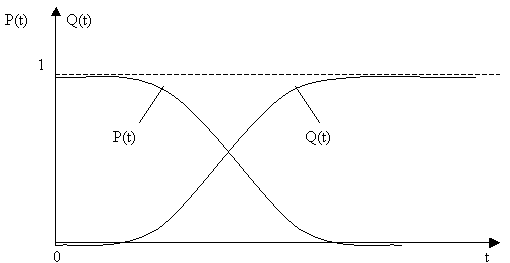
Рис. 2.2 Зависимости P(t) и Q(t) от наработки
Практический интерес представляет определение ВБР в интервале наработки [t, t + Δt], при условии, что объект безотказно проработал до начала t интервала. Определим эту вероятность, используя теорему умножения вероятностей, и выделив следующие события:
A = {безотказная работа объекта до момента t};
B = {безотказная работа объекта в интервале Δt};
C = A·B = {безотказная работа объекта до момента t + Δt}.
Очевидно B(C) = P(A·B) = P(A)·P(B| A), поскольку события A и B будут зависимыми.
Условная вероятность P(B| A) представляет ВБР P(t, t + Δt) в интервале [t, t + Δt], поэтому
P(B| A) = P(t, t + Δt) = P(C)/ P(A) = P(t + Δt)/ P(t). (2.6)
ВО в интервале наработки [t, t + Δt], с учетом (6), равна:
Q( t, t + Δt ) = 1 - P( t, t + Δt ) = [ P(t ) - P(t + Δt ) ] / P(t ). (2.7)
Плотность распределения отказов (ПРО)
Статистическая оценка ПРО определяется отношением числа объектов n(t, t + Δt), отказавших в интервале наработки [t, t + Δt] к произведению общего числа объектов N на длительность интервала наработки Δt.
![]() (2.8)
(2.8)
Поскольку ∆n ( t, t + Δt ) = n ( t + Δt ) - n(t), где n(t + Δt ) – число объектов, отказавших к моменту наработки t + Δt, то оценку ПРО можно представить:
![]() (2.9)
(2.9)
где
![]() – оценка ВО в интервале наработки, т.
е. приращение ВО заΔt.
– оценка ВО в интервале наработки, т.
е. приращение ВО заΔt.
Оценка ПРО представляет «частоту» отказов, т. е. число отказов за единицу наработки, отнесенное к первоначальному числу объектов.
Вероятностное определение ПРО следует из (2.9) при стремлении интервала наработки Δt → t0 и увеличения объема выборки N → ∞