Файл: Крюков В.Г. Основы работоспособности технических систем.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.10.2024
Просмотров: 367
Скачиваний: 0
СОДЕРЖАНИЕ
Кафедра Автомобильных Двигателей и Сервиса
Тема 1. Технические системы: качество, работоспособность, диагностика
1.1 Техническая система и ее жизненный цикл
1.2 Качество и работоспособность технических систем.
Понятие о техническом состоянии автомобиля.
Причины и последствия изменения технического состояния
1.3 Работоспособность и диагностика технической системы
Оценка работоспособности технической системы.
Рис 1.4 Прямые и косвенные методы определения рабочих параметров Свойства диагностических параметров
Тема 2 показатели и характеристики надежности
2.1 Основные понятия надежности. Классификация отказов Основные понятия
Классификация и характеристики отказов
2.2 Количественные показатели безотказности
2.3 Связи показателей надежности. Характеристики безотказности
3.1 Общие понятия. Статистическая обработка испытаний
3.2 Нормальный закон распределения наработки до отказа Классическое нормальное распределение.
3.3 Законы распределения наработки до отказа
3.4 Надежность систем. Общие понятия и определения
Рис 3.13 Примеры ненагруженного резервирования
3.5 Надежность основной системы
Тема 4. Сбор информации и идентификация моделей
4.1. Методы сбора информации о надежности автомобиля.
4.2. Идентификация работы двигателя по результатам стендовых испытаний:
4.3 Моделирование работы двигателя в эксплуатации
Тема 5 производительность средств обслуживания
5.1. Предприятия технического обслуживания и смо
5.2 Системы массового обслуживания с отказами
5.3 Система массового обслуживания с ожиданием
Тема 6. Управление станциями технического обслуживания автомобилей
![]() (3.39)
(3.39)
- вероятность отказа (ВО) основной системы (ОС):
![]() (3.40)
(3.40)
При идентичных элементах ОС: P1(t) = … = Pn(t) = P(t), тогда:
- вероятность безотказной работы: Pс(t) = Pn(t);
- вероятность отказа: Qс(t) = 1 - Pn(t).
Поскольку на участке нормальной эксплуатации наработку до отказа можно описать экспоненциальным распределением каждого элемента
Pi(t) = exp( -λi·t), (3.41)
![]() (3.42)
(3.42)
где λi = const, то вероятность безотказной работы ОС определяется по формуле:
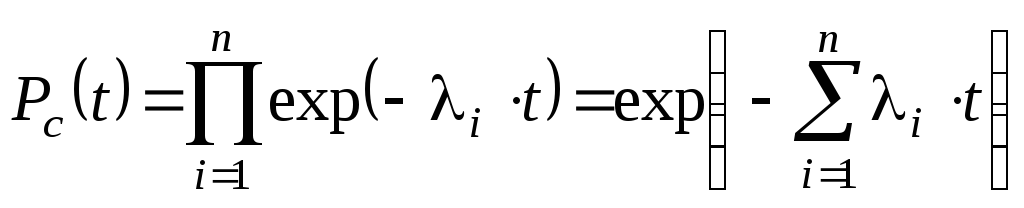 (3.43)
(3.43)
Отсюда,
полагая
![]() получаем,
что интенсивность отказов ОС равна
сумме интенсивностей отказов элементов
получаем,
что интенсивность отказов ОС равна
сумме интенсивностей отказов элементов
![]() (3.44)
(3.44)
В общем случае, для любого распределения наработки интенсивность отказов системы равна:
![]() (3.45)
(3.45)
отсюда
для n
идентичных элементов
![]() получим:
получим:
![]() (3.46)
(3.46)
Если
![]() не
меняется со временем (
не
меняется со временем (![]() )
то при экспоненциальном распределении
наработки до отказа каждого элемента
)
то при экспоненциальном распределении
наработки до отказа каждого элемента![]() ,
показатели безотказности ОС определяются
для:
,
показатели безотказности ОС определяются
для:
- вероятность безотказной работы и вероятность отказа:
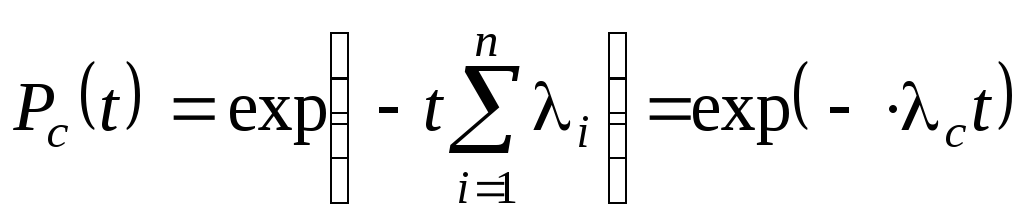
![]() (3.47)
(3.47)
- интенсивность отказа и МО наработки до отказа:
![]()
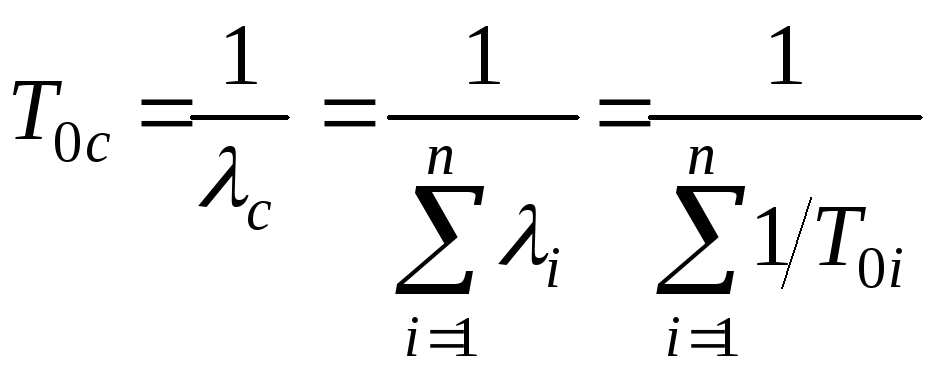 (3.48)
(3.48)
Плотность распределения отказов:
fс(t) = - d Pс(t)/ dt = λс exp( -λс·t); (3.49)
Таким образом, при экспоненциальной наработке до отказа каждого из n элементов, распределение наработки до отказа ОС также подчиняется экспоненциальному распределению. Для ОС надежность меньше надежности каждого из элементов. С увеличением числа элементов надежность ОС уменьшается. Например, при n = 1000, Pi(t) = 0,99, Pс(t) < 10-4 и средняя наработка до отказа системы в 1000 раз меньше средней наработки каждого из элементов.
Распределение норм надежности основной системы по элементам.
Рассмотренные модели позволяют определить показатели безотказности ОС по известным показателям надежности элементов – так решается задача при завершении технического проекта, после испытаний опытных образцов системы и составляющих элементов. Для этого случая: значения Pi(t) i–тых элементов хорошо известны и значение Pс(t)лишь уточняется и сравнивается с заданным в ТЗ на проект. При этом, еслиPс(t)получается меньшей, чем в ТЗ, то принимаются меры по ее повышению (резервирование, использование более надежных элементов и т. п.).
Но на начальной стадии проектирования в ТЗ указывается лишь ВБР проектируемой системы и тогда при проектировании используются как элементы с известной надежностью, так и элементы, о надежности которых можно судить лишь по их аналогам (прототипам). При этом необходима предварительная оценка надежности элементов, которая, в дальнейшем, уточняется в ходе испытания опытных образцов системы и элементов. В этой ситуации применяются различные способы распределения норм надежности и выбор того или иного способа зависит от имеющейся информации о проектируемой системе.Среди них можно отметить следующие:
1. Распределение надежности по принципу равнонадежности элементов:
Здесь
обычно по техническому заданию заданы
Pс(t),
n – число
элементов системы и принимается, что
распределение наработки до отказа
элементов – экспоненциальное. Тогда
при идентичных (равнонадежных) элементах
(![]() )
интенсивность отказаi–го
элемента:
)
интенсивность отказаi–го
элемента:
![]() (3.50)
(3.50)
2. Распределение надежности с учетом данных о надежности аналогов.
Здесь
по техническому заданию заданы: Pс(t),
n
– число элементов системы и интенсивности
отказов аналогов –
![]() .Сначала
определяется доля отказов системы из-за
отказовi–го
элемента:
.Сначала
определяется доля отказов системы из-за
отказовi–го
элемента:
![]() (3.51)
(3.51)
где
![]() -интенсивность
отказов системы по данным об аналогах.
-интенсивность
отказов системы по данным об аналогах.
Далее
определяется ИО проектируемой системы:
![]() и требуемая
интенсивность отказов составляющих
элементов:
и требуемая
интенсивность отказов составляющих
элементов: ![]() .
.
3.Распределение надежности с учетом перспектив совершенствования элементов.
Здесь по техническому заданию заданы Pс(t), n – число элементов системы, а также изменение ИО аналогов за временной период [τ = 19XY по 200Z годы], аппроксимированное выражением :
λаiτ = φ(λаi , 19XY, τ), (3.52)
где λаi – - интенсивность отказов i–го аналога в 19XY году.
По этой формуле значение аналога λаiτ экстраполируется до года проектирования системы (τр) откуда получаются: λа1(τр),…, λаi(τр ), далее определяется доля отказов системы из-за отказов i–го элемента:
![]() (3.53)
(3.53)
и
интенсивность отказов элементов системы
по формуле![]() гдеλс
определяется
по формуле (3.50).
гдеλс
определяется
по формуле (3.50).
Контрольные вопросы:
1. Что представляет математическая модель, и для каких целей она используется в задачах надежности?
2. Из каких условий выбирается закон распределения наработки до отказа объекта?
3. В чем заключается постановка задачи при испытаниях объектов на надежность?
4. Что представляет собой процедура формирования статистического ряда по результатам испытаний?
5. Какие эмпирические функции рассчитываются при обработке результатов испытаний?
6. В чем заключается выбор закона распределения наработки до отказа по результатам испытаний?
7. Что представляет собой критерий согласия?
8. Объясните, почему распределение Гаусса называется нормальным?
9. Поясните на изменении кривой плотности распределения отказов влияние параметров распределения математического ожидания и дисперсии?
10. Приведите расчетные выражения для показателей безотказности, определенные через табличные функции f(x), F(x) и Φ(x)?
11. При каких условиях корректно использовать классическое нормальное распределение, и в каких случаях целесообразно применять усеченные нормальные распределения?
12. Приведите расчетные выражения показателей безотказности для усеченного «слева» нормального распределения?
13. Наработка до отказа серийно выпускаемой детали распределена нормально с параметрами: Т0 = M(T) = 104 час, S = S (T) = 250 час. Определить:
1) вероятность того, что при монтаже прибора в него будут поставлены детали, наработка до отказа которых будет находиться в интервале [5000, 9000 час];
2) вероятность того, что при монтаже прибора в него будут поставлены детали, наработка до отказа которых будет находиться в интервале [Т0 - 3S, Т0 + 3S];
3) вероятность того, что безотказно проработав до момента времени 5000 час, деталь безотказно проработает и до 9000 час?
Ответы: 1) 0.00003, 2) 0.9974, 3) 0.99997.
14. Комплектующая деталь, используемая при изготовлении устройства, по данным поставщика этой детали имеет нормальное распределение наработки с параметрами:
Т0 = 4 · 103 час, S = 800 час. Определить интересующую конструктора прибора:
1) наработку до отказа, соответствующую 90% надежности детали;
2) вероятность того, что при монтаже деталь имеет наработку, лежащую в интервале [2.5 · 103, 3 · 103];
3) вероятность того, что при монтаже деталь имеет наработку, большую, чем 2.5 103 час?
Ответы: 1) 2974.4, 2) 0.0755, 3) 0.9699.
15. .Как описывается изменение плотности распределения отказов при экспоненциальном распределении наработки до отказа?
16. .Получите расчетное выражение для ВБР, ВО и ИО при экспоненциальном распределении наработки до отказа?
17. Как связаны числовые характеристики наработки до отказа с интенсивностью отказов при экспоненциальном распределении наработки до отказа?
18. Для описания надежности каких объектов используется логарифмически-нормальное распределение?
19. Какой из параметров в выражении плотности распределения отказов при гамма-распределении наработки является параметром формы и параметром масштаба?
20. Известно, что серийно выпускаемая деталь имеет экспоненциальное распределение наработки до отказа с параметром λ = 10-5 час-1. Деталь используется конструктором при разработке нового прибора. Назначенный ресурс прибора предполагается Tн = 104 час. Определить интересующую конструктора:
1) среднюю наработку детали до отказа;
2) вероятность того, что деталь безотказно проработает в интервале наработки [0, Tн];
3)вероятность того, что деталь безотказно проработает в интервале наработки [103, 104 час]?
Ответы: 1) 105 час, 2) 0.905, 3) 0.914.
21. На сборку прибора поступила деталь, прошедшая испытания на надежность. Известно, что наработка до отказа детали подчиняется экспоненциальному распределению с параметром λ = 5 10-5 час-1. Определить вероятность того, что при монтаже прибора в него будут поставлены детали, наработка до отказа которых будет находиться в интервале [103, 104час]?
Ответ: 0.345.
22. Основные цели и задачи расчета показателей надежности систем?
23. Определите состав рассчитываемых показателей безотказности системы?
24. Перечислите и поясните основные этапы расчета надежности систем?
25. Что такое структурная схема надежности?
26. Что такое математическая модель расчета надежности?
27. Какие виды резервирования существуют. В чем отличие нагруженного и ненагруженного резервирования?
28. Что такое кратность резервирования и в чем отличие целой и дробной кратности?
29. Что такое основная система и в чем состоит условие ее безотказной работы?
30. Как определяются показатели безотказности основной системы: ВБР и ИО?
31. Как определяются показатели безотказности основной системы: ПРО и МО наработки до отказа?
32. Какой закон распределения наработки до отказа будет иметь основная система, если законы распределения наработки до отказа элементов являются экспоненциальными (привести доказательство)?
33. В чем заключается необходимость распределения норм надежности между элементами основной системы?