Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 264
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
W(p). Значит, искомая передаточная функция есть
.
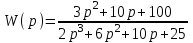Комплексные полиномы имеют вид:
В(p) = 3p2 + 10p + 100,
D(p) = 2p3 + 6p2 + 10p +25.
Характеристическое уравнение получается, если приравнять нулю комплексный полином знаменателя передаточной функции:
2p3 + 6p2 + 10p + 25 = 0.
2.2. Частотные характеристики
Передаточная функция выражает свойства системы через комплексную переменную, которая содержит действительную и мнимую части: p = σ + jω. Мнимая часть имеет смысл циклической частоты колебаний. Если взять чисто мнимое значение комплексной переменной, p = jω, и ввести эту величину в передаточную функцию (2.6), получается частотная функция:
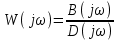. (2.8)
Ее называют комплексная частотная характеристика, амплитудно-фазовая частотная характеристика, комплексный коэффициент усиления.
По определению, она записывается отношением частотных полиномов. Но возможны и другие формы записи. Обратим внимание на то, что частотный полином В(jω) в развернутом виде,
,
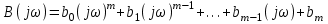представляет собой сумму действительной и мнимой частей:
.
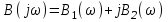Так получается потому, что j =
в четной степени будет либо – 1, либо + 1.
Частотный полином D(jω) в развернутом виде имеет ту же структуру:
D(jω) = D1(ω) + jD2(ω),
следовательно, комплексная частотная характеристика есть отношение двух комплексных чисел:
.
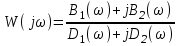Умножение числителя и знаменателя на число, сопряженное знаменателю, позволяет выделить действительную и мнимую части:
.
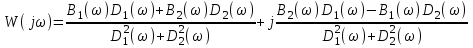Первое слагаемое обозначим U(ω), второе V(ω). U(ω) называют действительной частотной характеристикой, V(ω) - мнимой частотной характеристикой. В краткой записи
W(jω) = U(ω) + jV(ω). (2.9)
Комплексное выражение (2.9) можно интерпретировать геометрически, отложив по оси абсцисс действительную частотную характеристику, по оси ординат – мнимую частотную характеристику, рис. 2.1.
Рис. 2.1. Геометрическая интерпретация W(jω)
Для заданной частоты U(ω) и V(ω) – пара чисел, определяющих положение точки М на плоскости. Соединив прямой А начало координат с точкой М, получим прямоугольный треугольник. Для него справедливы соотношения: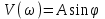
, 
,
, 
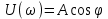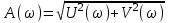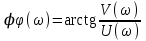. (2.10)
Все величины – функции частоты ω.
Комплексную частотную характеристику, следовательно, можно записать в виде
W(j ω) = U(ω) + jV(ω) = A (cos ( ω) + j sin(ω)).
По формуле Эйлера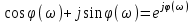
. Поэтому
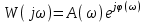. (2.11)
А(ω) называют амплитудной частотной характеристикой или просто амплитудой.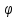
(ω) называют фазовой частотной характеристикой или просто фазой.
Для практических расчетов широко применяются логарифмические частотные характеристики. Их две: логарифмическая амплитудная частотная характеристика (ЛАЧХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ).
ЛАЧХ называют графическое представление функции
L(ω) = 20 lg A(ω)
в зависимости от lg ω. Точнее, не самой функции, а ее асимптотических приближений в виде отрезков прямых. Асимптоты находят для области ω< 1 и для области ω> 1. Прямые строят по точкам пересечения с осями координат и между собой.
Для построения графика ЛФЧХ по ординате откладывают фазу, по абсциссе – соответствующий ей lg ω.
П
ример 2.2.
Записать комплексную частотную характеристику, частотные характеристики, амплитуду и фазу для системы, описываемой дифференциальным уравнением
.
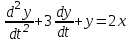Преобразуя по Лапласу, получаем операторное уравнение
(p2 + 3p + 1) Y
(p) = 2 X(p)
и передаточную функцию:
.
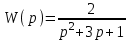Подстановкой p= jω превращаем передаточную функцию в комплексную частотную характеристику:
.
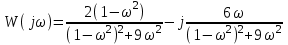Действительная частотная характеристика
.
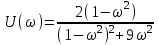Мнимая частотная характеристика
.
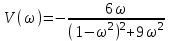Амплитуда
.
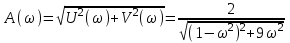Фаза
.
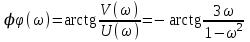П
ример 2.3.
Найти комплексную частотную характеристику, амплитуду и фазу пропорционально-интегрального регулятора ( ПИ - регулятора ). Его уравнение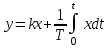
.
(T – постоянная времени, k – коэффициент усиления).
Продифференцируем исходное уравнение,
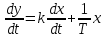
и преобразуем по Лапласу:
.
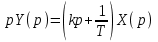Из операторного уравнения составим передаточную функцию:
.
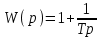Полагая p = jω, записываем комплексную частотную характеристику
,
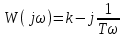находим частотные характеристики:
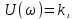
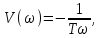
и амплитудную частотную характеристику:
.
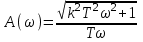Фаза в функции частоты имеет выражение
.
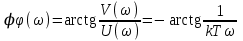П
ример 2.4.
Найти логарифмическую амплитудную частотную характеристику ПИ - регулятора.
Воспользуемся выражением для амплитуды и запишем общий вид ЛАЧХ:
L(ω) = 20 lg A(ω) = 10 lg(k2T2ω2 + 1) – 20 lg Tω.
Выделим асимптотические прямые.
В области ω < 1. С уменьшением ω слагаемое k2T2ω2 становится пренебрежимо меньше единицы. Его можно отбросить. Тогда первый член L(ω) обращается в нуль вследствие lg 1 = 0. Остается
L1 = – 20 lgT – 20 lg ω.
L2 = 20 lg k + 20 lg Tω - 20 lg Tω = 20 lg k.
Для построения графика надо найти точки пересечения прямой L1 c осями координат и с прямой L2. (По ординате откладывают L1, L2, по абсциссе lg ω).
Точка пересечения с осью ординат находится из условия lg ω = 0. Получается: L1 = – 20 lg T = 20 lg (1/T).
Точка пересечения с осью абсцисс находится из условия L1 = 0. Получается: lg ω = lg (1/T).
Точка пересечения прямой L1 с прямой L2 находится из условия L1 = L2. Получается: lg ω = lg (1/kT).
Вид графика показан на рис. 2.1.
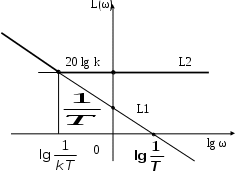
Рис. 2.2. Асимптотическая логарифмическая
амплитудная частотная характеристика ПИ - регулятора
2.3. Математические модели
входных воздействий
В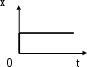
дифференциальном уравнении (2.1) правая часть есть сумма воздействующего на вход системы сигнала x(t) и его производных. В реальных условиях на вход системы воздействуют сигналы произвольного характера. То есть, математически они описываются произвольными зависимостями входной величины от времени.
Однако, в теоретических исследованиях принимают, что воздействия оказываются в виде единичного скачка, единичного импульса, гармонического колебания, сигнала постоянной скорости. Эти воздействия называют типовыми. Рис. 2.3. График
ступенчатой функции
Ступенчатая функция (единичный скачок). В момент t= 0 воздействие мгновенно достигает величины x= 1, далее со временем не меняется. График показан на рис. 2.3.
Единичную ступенчатую функцию записывают символом 1(t). Значения:
t 0 1(t) = 0,
t = 0 1(t) = 1,
t 0 1(t) = 1.
Если воздействие ступенчатое, но отличается от единичного в А раз, его обозначают А(1). А(1) = А1(t
).
Импульсная функция (единичный импульс). Это такой импульс величина которого равна бесконечности, длительность - нулю, а площадь – единице. В математике известен как дельта функция. Обозначается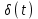
. Значения:
t 0 δ(t) = 0,
t = 0 δ(t) = ∞,
t 0 δ(t) = 0.
Единичный импульс есть производная от единичной ступенчатой функции:
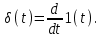
Импульсную функцию можно трактовать как предел прямоугольного импульса, у которого высота стремится к ∞, а время его действия – к нулю.
Гармоническая функция. Это функция, изменяющаяся по закону синуса или косинуса.
Записывается либо как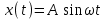
либо как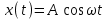
.
Величина воздействия колеблется между значениями A и - A.
Линейная функция.
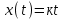
Воздействие возрастает пропорционально времени.
Квадратичная функция.
.
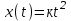Воздействие возрастает пропорционально квадрату времени.
2.4. Переходная функция
С момента воздействия x(t) на вход системы, управляемая величина y(t) начинает изменяться. Процесс, происходящий в это время, называют переходным. Аналитическая зависимость y(t), описывающая переходной процесс, называется переходной функцией. Будет система управляться лучше или хуже – зависит от переходной функции.
Переходной процесс обуславливается внутренними свойствами системы и видом воздействия. Чтобы иметь возможность сравнивать переходные процессы разных систем, принято оказывать воздействие в виде единичной ступенчатой функции при нулевых начальных условиях. Переходную функцию обозначают h(t).
Первую производную от переходной функции называют весовой функцией и обозначают w(t).
Переходные функции подразделяются на три вида в зависимости от того, как ведет себя производная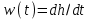
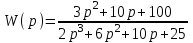.Комплексные полиномы имеют вид:
В(p) = 3p2 + 10p + 100,
D(p) = 2p3 + 6p2 + 10p +25.
Характеристическое уравнение получается, если приравнять нулю комплексный полином знаменателя передаточной функции:
2p3 + 6p2 + 10p + 25 = 0.
2.2. Частотные характеристики
Передаточная функция выражает свойства системы через комплексную переменную, которая содержит действительную и мнимую части: p = σ + jω. Мнимая часть имеет смысл циклической частоты колебаний. Если взять чисто мнимое значение комплексной переменной, p = jω, и ввести эту величину в передаточную функцию (2.6), получается частотная функция:
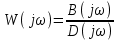. (2.8)Ее называют комплексная частотная характеристика, амплитудно-фазовая частотная характеристика, комплексный коэффициент усиления.
По определению, она записывается отношением частотных полиномов. Но возможны и другие формы записи. Обратим внимание на то, что частотный полином В(jω) в развернутом виде,
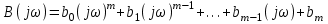,представляет собой сумму действительной и мнимой частей:
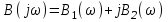.Так получается потому, что j =
в четной степени будет либо – 1, либо + 1.Частотный полином D(jω) в развернутом виде имеет ту же структуру:
D(jω) = D1(ω) + jD2(ω),
следовательно, комплексная частотная характеристика есть отношение двух комплексных чисел:
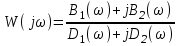.Умножение числителя и знаменателя на число, сопряженное знаменателю, позволяет выделить действительную и мнимую части:
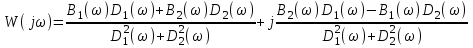.Первое слагаемое обозначим U(ω), второе V(ω). U(ω) называют действительной частотной характеристикой, V(ω) - мнимой частотной характеристикой. В краткой записи
W(jω) = U(ω) + jV(ω). (2.9)
Комплексное выражение (2.9) можно интерпретировать геометрически, отложив по оси абсцисс действительную частотную характеристику, по оси ординат – мнимую частотную характеристику, рис. 2.1.
Рис. 2.1. Геометрическая интерпретация W(jω)
Для заданной частоты U(ω) и V(ω) – пара чисел, определяющих положение точки М на плоскости. Соединив прямой А начало координат с точкой М, получим прямоугольный треугольник. Для него справедливы соотношения:
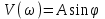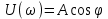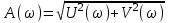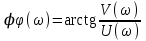, , , . (2.10)Все величины – функции частоты ω.
Комплексную частотную характеристику, следовательно, можно записать в виде
W(j ω) = U(ω) + jV(ω) = A (cos ( ω) + j sin(ω)).
По формуле Эйлера
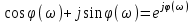. Поэтому 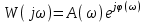. (2.11)А(ω) называют амплитудной частотной характеристикой или просто амплитудой.
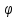(ω) называют фазовой частотной характеристикой или просто фазой.Для практических расчетов широко применяются логарифмические частотные характеристики. Их две: логарифмическая амплитудная частотная характеристика (ЛАЧХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ).
ЛАЧХ называют графическое представление функции
L(ω) = 20 lg A(ω)
в зависимости от lg ω. Точнее, не самой функции, а ее асимптотических приближений в виде отрезков прямых. Асимптоты находят для области ω< 1 и для области ω> 1. Прямые строят по точкам пересечения с осями координат и между собой.
Для построения графика ЛФЧХ по ординате откладывают фазу, по абсциссе – соответствующий ей lg ω.
П
ример 2.2.
Записать комплексную частотную характеристику, частотные характеристики, амплитуду и фазу для системы, описываемой дифференциальным уравнением
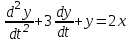.Преобразуя по Лапласу, получаем операторное уравнение
(p2 + 3p + 1) Y
(p) = 2 X(p)
и передаточную функцию:
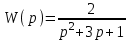.Подстановкой p= jω превращаем передаточную функцию в комплексную частотную характеристику:
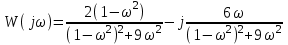.Действительная частотная характеристика
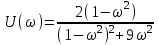.Мнимая частотная характеристика
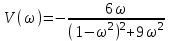.Амплитуда
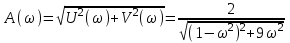.Фаза
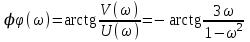.П
ример 2.3.
Найти комплексную частотную характеристику, амплитуду и фазу пропорционально-интегрального регулятора ( ПИ - регулятора ). Его уравнение
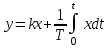.(T – постоянная времени, k – коэффициент усиления).
Продифференцируем исходное уравнение,
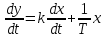
и преобразуем по Лапласу:
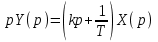.Из операторного уравнения составим передаточную функцию:
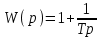.Полагая p = jω, записываем комплексную частотную характеристику
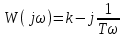,находим частотные характеристики:
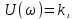
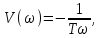
и амплитудную частотную характеристику:
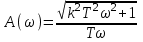.Фаза в функции частоты имеет выражение
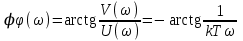.П
ример 2.4.
Найти логарифмическую амплитудную частотную характеристику ПИ - регулятора.
Воспользуемся выражением для амплитуды и запишем общий вид ЛАЧХ:
L(ω) = 20 lg A(ω) = 10 lg(k2T2ω2 + 1) – 20 lg Tω.
Выделим асимптотические прямые.
В области ω < 1. С уменьшением ω слагаемое k2T2ω2 становится пренебрежимо меньше единицы. Его можно отбросить. Тогда первый член L(ω) обращается в нуль вследствие lg 1 = 0. Остается
L1 = – 20 lgT – 20 lg ω.
В области ω > 1. В первом слагаемом следует пренебречь единицей. В таком случае
L2 = 20 lg k + 20 lg Tω - 20 lg Tω = 20 lg k.
Для построения графика надо найти точки пересечения прямой L1 c осями координат и с прямой L2. (По ординате откладывают L1, L2, по абсциссе lg ω).
Точка пересечения с осью ординат находится из условия lg ω = 0. Получается: L1 = – 20 lg T = 20 lg (1/T).
Точка пересечения с осью абсцисс находится из условия L1 = 0. Получается: lg ω = lg (1/T).
Точка пересечения прямой L1 с прямой L2 находится из условия L1 = L2. Получается: lg ω = lg (1/kT).
Вид графика показан на рис. 2.1.
Рис. 2.2. Асимптотическая логарифмическая
амплитудная частотная характеристика ПИ - регулятора
2.3. Математические модели
входных воздействий
В
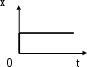дифференциальном уравнении (2.1) правая часть есть сумма воздействующего на вход системы сигнала x(t) и его производных. В реальных условиях на вход системы воздействуют сигналы произвольного характера. То есть, математически они описываются произвольными зависимостями входной величины от времени. Однако, в теоретических исследованиях принимают, что воздействия оказываются в виде единичного скачка, единичного импульса, гармонического колебания, сигнала постоянной скорости. Эти воздействия называют типовыми. Рис. 2.3. График
ступенчатой функции
Ступенчатая функция (единичный скачок). В момент t= 0 воздействие мгновенно достигает величины x= 1, далее со временем не меняется. График показан на рис. 2.3.
Единичную ступенчатую функцию записывают символом 1(t). Значения:
t 0 1(t) = 0,
t = 0 1(t) = 1,
t 0 1(t) = 1.
Если воздействие ступенчатое, но отличается от единичного в А раз, его обозначают А(1). А(1) = А1(t
).
Импульсная функция (единичный импульс). Это такой импульс величина которого равна бесконечности, длительность - нулю, а площадь – единице. В математике известен как дельта функция. Обозначается
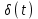. Значения:t 0 δ(t) = 0,
t = 0 δ(t) = ∞,
t 0 δ(t) = 0.
Единичный импульс есть производная от единичной ступенчатой функции:
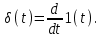
Импульсную функцию можно трактовать как предел прямоугольного импульса, у которого высота стремится к ∞, а время его действия – к нулю.
Гармоническая функция. Это функция, изменяющаяся по закону синуса или косинуса.
Записывается либо как
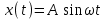
либо как
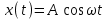.Величина воздействия колеблется между значениями A и - A.
Линейная функция.
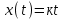
Воздействие возрастает пропорционально времени.
Квадратичная функция.
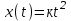.Воздействие возрастает пропорционально квадрату времени.
2.4. Переходная функция
С момента воздействия x(t) на вход системы, управляемая величина y(t) начинает изменяться. Процесс, происходящий в это время, называют переходным. Аналитическая зависимость y(t), описывающая переходной процесс, называется переходной функцией. Будет система управляться лучше или хуже – зависит от переходной функции.
Переходной процесс обуславливается внутренними свойствами системы и видом воздействия. Чтобы иметь возможность сравнивать переходные процессы разных систем, принято оказывать воздействие в виде единичной ступенчатой функции при нулевых начальных условиях. Переходную функцию обозначают h(t).
Первую производную от переходной функции называют весовой функцией и обозначают w(t).
Переходные функции подразделяются на три вида в зависимости от того, как ведет себя производная