ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 516
Скачиваний: 1
СОДЕРЖАНИЕ
Требования к уровню освоения содержания дисциплины
Количество информации как мера уменьшения неопределенности знаний
Алфавитный подход к определению количества информации
Характеристики основных типов данных
Кодирование числовой информации в компьютере
Кодирование текстовой информации в компьютере
Кодирование графической информации в компьютере
Кодирование аудио информации в компьютере
ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
Вопросы для самопроверки по теме 2
3. ТЕХНИЧЕСКИЕ СРЕДСТВА РЕАЛИЗАЦИИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
Принципы работы электронной вычислительной
ПРОГРАММНЫЕ СРЕДСТВА РЕАЛИЗАЦИИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
Файловая структура ОС. Операции с файлами
Инструментальное программное обеспечение ЭВМ
Основные понятия алгоритмических языков. Алфавит.
Прикладное программное обеспечение ЭВМ
Вопросы для самопроверки по теме 4
МОДЕЛИ РЕШЕНИЯ ФУНКЦИОНАЛЬНЫХ И ВЫЧИСЛИТЕЛЬНЫХ ЗАДАЧ
АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ
Вопросы для самопроверки по теме 6
7. ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ
Основные принципы структурного программирования (программирование без GO TO)
Этапы решения задач на компьютере
ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СЕТИ ЭВМ МЕТОДЫ ЗАЩИТЫ ИНФОРМАЦИИ
Электронно-цифровая подпись (ЭЦП)
Классификация антивирусных программ
Вопросы для самопроверки по теме 8
ОТВЕТЫ НА ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- 1 ... 8 9 10 11 12 13 14 15 ... 45
ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
-
Основные понятия алгебры логики
Алгебра логики – это раздел математики, изучающий логиче- ские высказывания и логические операции над ними.
Логическоевысказывание – это любое повествовательное предложение, про которое можно однозначно сказать, истинно оно или ложно. Примеры: «студент 1501 группы», «в городе более мил- лиона жителей» (без указания названия города) – не являются логи- ческими высказываниями. «Иванов – студент 1501 группы и живет в Санкт-Петербурге», «в городе Санкт-Петербурге более миллиона жи- телей» – это логические высказывания.
Слова и словосочетания «не», «и», «или», «если…, то», «тогда и только тогда» называются логическими связками. С их помощью формируются составные высказывания из более простых. Элемен-тарные высказывания – не содержат в себе других высказываний. В предыдущих примерах «в городе Санкт-Петербурге более миллиона жителей» – элементарное высказывание, а «Иванов – студент 1501 группы и живет в Санкт-Петербурге» – составное, так как его можно разбить на два более простых: «Иванов – студент 1501 группы»,
«Иванов живет в Санкт-Петербурге».
Для того чтобы исследовать общие характеристики высказы- ваний и упростить их запись и анализ, абстрагируясь от предметной области, к которой они относятся, их обозначают буквами латинского алфавита, и рассматривают как логические переменные, принимаю-
щие только два значения: «истина» и «ложь». Например, для приве- денных выше примеров:
А = «Иванов – студент 1501 группы»;
В = «Иванов живет в Санкт-Петербурге»;
А и В = «Иванов – студент 1501 группы и живет в Санкт- Петербурге».
-
Основные логические операции
Каждая логическая связка рассматривается как операция, ре- зультат которой зависит от значений входящих в неѐ переменных (то есть высказываний). Для упрощения записи вместо слов «истина» и
«ложь» используют двоичные цифры: «истина» = 1, «ложь» = 0. Ос-

новные логические операции и их результаты при разных значениях высказываний приведены в табл.2.1.
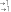
 Таблица 2.1 Основные логические операции (иерархия сверху вниз):
Таблица 2.1 Основные логические операции (иерархия сверху вниз):| Название | Обозначение | Результат |
| Отрицание, инверсия (связка «не») | А, | А = 0 А = 1 А = 1 А = 0 |
| Конъюнкция, лог. умножение (связ- ка «и») | А В, А & В, А ^ В | А = 1, В = 1 А В = 1, в остальных случаях – = 0 |
| Дизъюнкция, лог. Сложение (связка «или» | А v В, А + В | А = 0, В = 0 А v В = 0, в остальных случаях – = 1 |
| | | |
| Импликация (связки «если…, то», «из… следует», … влечѐт…» | А В | А = 1, В = 0, то А В = 0, в остальных случаях = 1 |
| Эквиваленция, двойная импликация (связки «тогда и только тогда», «необходимо и достаточно», «…равносильно…», | А В; А В | А = 1, В = 1 А В = 1 А = 0, В = 0 А В = 1 А = 1, В = 0 А В = 0 А = 0, В = 1 А В = 0 |
 Анализ составных логических высказываний удобно делать с помощью таблиц истинности. В них представляют все возможные комбинации значений элементарных высказываний, которые входят в составное, и его результирующее значения для каждой из них. При- меры:
Анализ составных логических высказываний удобно делать с помощью таблиц истинности. В них представляют все возможные комбинации значений элементарных высказываний, которые входят в составное, и его результирующее значения для каждой из них. При- меры:| Конъюнкция | ||
| А | В | F =А В |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| Дизъюнкция | ||
| А | В | F =А+В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| Импликация | ||
| А | В | F = А В |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| Эквиваленция | ||
| А | В | F = А В |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

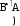 Анализ логического высказывания А и не В и не А (A
Анализ логического высказывания А и не В и не А (A-
А
В
Y1 = А
Y2 = В
Y3 = А Y2
Y4 = Y3 Y1
0
0
1
1
0
0
0
1
1
0
0
0
1
0
0
1
1
0
1
1
0
0
0
0
Ответ: выражение тождественно ложно.
 Анализ логического высказывания А и не А или В (A А v B)
Анализ логического высказывания А и не А или В (A А v B)-
А
В
Y1 = А
Y2 = А Y1
Y3 = Y2 v В
0
0
1
0
0
0
1
1
0
1
1
0
0
0
0
1
1
0
0
1