Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

- учитывая, что объем товарооборота представляет собой абсолютный стои­мостный показатель, для расчета скользящего среднего соз­дадим в разработочной таблице колонку относительных ве­личин, характеризующих динамику товарооборота предпри­ятия — цепных темпов прироста (вводим в ячейку С4 формулу =В4/В3*100-100 и копируем ее в ячейки С5:С18) (столбец С таблицы 3.10);

- вы­равнивание динамического ряда, состоящего из 15 цепных темпов прироста товарооборота, проведем, используя интер­вал усреднения, равный, например, 5. Для расчета показате­лей выровненного ряда (столбец D таблицы 3.10) воспользуемся другим способом создания скользящего среднего в Excel, т.е. прямым введением формулы в соответствующую ячей­ку рабочего листа. Так, чтобы получить пятимесячное сколь­зящее среднее цепных темпов прироста, в ячейку D8 таблицы 10 вводится формула =СРЗНАЧ(С4:С8). Затем эта формула с помощью средства Автозаполнение копируется и вставляет­ся в ячейки D9:D18;

- для составления прогноза товарооборота на 17-й месяц в таблице 3.10 необходимо занести еще три формулы: расчета среднего изменения темпов его прироста: =(D18-D8)/10 (ячейка Е18), расче­та прогнозируемого цепного темпа прироста на 17-й месяц: =D18+2*E18 (ячейка С20), расчета прогнозируемого объема товарооборо­та: B18*(C20+100)/100 (ячейка В20). Результатом всех проведенных операций становится итоговая таблица 3.11, содержащая все промежуточ­ные элементы и значения единой цепи составления прогноза товарооборота.
Таблица 3.11 - Прогноз товарооборота на основе скользящего среднего средствами Excel (итоговая таблица)

	А	В	С	D	Е
1
2	Порядковый номер месяца	Объем товарооборота, ден. ед.	Цепные темпы прироста, %	Показатели выравненного ряда	Среднее изменение темпов прироста
3	1	28415
4	2	28231	-0,648	#Н/Д
5	3	29783	5,498	#Н/Д
6	4	30969	3,982	#Н/Д
7	5	30494	-1,534	#Н/Д
8	6	29757	-2,417	0,976
9	7	30850	3,673	1,840
10	8	31325	1,540	1,049
11	9	31359	0,109	0,274
12	10	31610	0,800	0,741
13	11	32366	2,392	1,703
14	12	33313	2,926	1,553
15	13	33508	0,585	1,362
16	14	33374	-0,400	1,261
17	15	34811	4,306	1,962
18	16	36046	3,548	2,193	0,122
19	Прогноз
20	17	36924	2,436

---

Задание 6. Использование функции ЛИНЕЙН для создания модели тренда

Составить прогноз товарооборота торгового пред­приятия по данным таблицы 3.6 с помощью функции ЛИНЕЙН.

Выполнение:

Функция рабочего листа ЛИНЕЙН помогает определить характер линейной связи между результатами наблюдений и временем их фиксации и дать ей математическое описание, наилучшим образом аппроксимирующее исходные данные. Для построения трендовой модели она использует уравнение вида у = mх + b, где у — исследуемый показатель; х = t— временной тренд; b, m — параметры уравнения, характери­зующие соответственно у-пересечение и наклон линии трен­да.

Вызвать функцию ЛИНЕЙН можно в диалоговом окне Мастера функций (категория «Статистические»), располо­женном на панели инструментов Стандартная.

Используя метод наименьших квадратов, функция ЛИНЕЙН создает массив значений, который описывает ис­комую модель тренда. Учитывая, что создается массив зна­чений, функция должна задаваться пользователем в виде формулы массива. Поэтому перед началом работы с ЛИ­НЕЙН необходимо на рабочем листе выделить диапазон яче­ек, достаточный для размещения создаваемого ею массива значений. Так, для прогнозирования товарооборота по дан­ным таблицы 3.6 обозначим ячейками E10:F14 диапазон для формирования выходного массива (таблица 3.12). После того, как выделен выходной диапазон и пользователь определился с аргументами функции посредством диалогового окна ЛИ­НЕЙН, следует нажать на клавиатуре кнопки Ctrl+Shift+Enter.
Таблица 3.12 - Расчет и оценка линейной модели тренда с помощью функции ЛИНЕЙН

	A	B	C	D	E	F
1
2	Порядковый номер месяца	Объем товарооборота, ден. ед.
3	1	28415
4	2	28231
5	3	29783
6	4	30969
7	5	30494
8	6	29757
9	7	30850
10	8	31325	Линейная оценка		437,425	27920,1
11	9	31359	Статистика		34,958505	338,033
12	10	31610			0,917921	644,603
13	11	32366			156,56746	14
14	12	33313			65055814	5817182
15	13	33508
16	14	33374
17	15	34811
18	16	36046

---

Функция ЛИНЕЙН имеет четыре аргумента (рисунок 3.11):

1) Известные значения у — это множество уже извес­тных значений исследуемого показателя, на основе которых будет производиться оценка параметров уравнения тренда. Так, при составлении прогноза товарооборота торгового пред­приятия по данным таблицы 3.6 известные значения у представ­лены в виде столбца и находятся в ячейках В3:В18;

2) Известные значения х — при построении трендовой модели представляют собой временной ряд, соответствую­щий по размерам первому аргументу. В нашем примере он находится в ячейках А3:А18 таблицы 3.6 и отражает порядко­вые номера месяца;

3) Конст — логическое значение, которое указывает на необходимость расчета параметра b (свободного члена) при построении модели тренда. Если Конст имеет значение ИСТИНА, то параметр b вычисляется. Если Конст имеет значение ЛОЖЬ, то параметр b принимается равным нулю;

4) Статистика — логическое значение, которое указы­вает на необходимость отражения на рабочем листе дополни­тельной статистической информации, позволяющей судить о качестве построенной модели. Если этот аргумент имеет зна­чение ЛОЖЬ или ссылка на него отсутствует, то функция ЛИНЕЙН не рассчитывает статистические характеристики. Если Статистика задана значением ИСТИНА, то мас­сив, создаваемый функцией, содержит значения следующих статистических величин (таблица 3.13).
Таблица 3.13 - Значения статистических величин функции ЛИНЕЙН

Стандартная ошибка для параметра m (COm)	Стандартная ошибка для свободного члена b (СОb)
Квадрат коэффициента корреляции (r2)	Стандартная ошибки для у (СОу)
F-критерий (F)	Степень свободы (df)
Сумма квадратов регрессии (SSp)	Остаточная сумма квадратов (SS0)

---

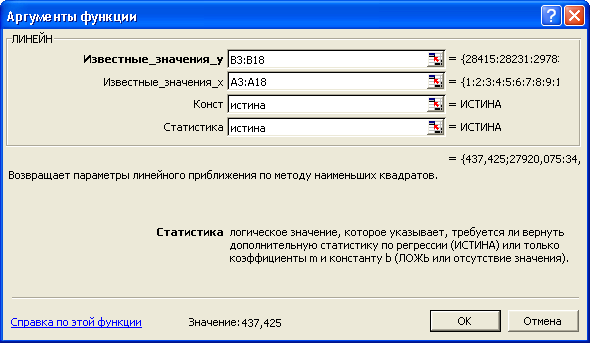
Рисунок 3.11 - Окно диалога функции ЛИНЕЙН
Вывод: Число в ячейке Е10 представляет собой наклон линии тренда (m = 437,425), а число в ячейке F10 — это у-пересечение прямой линии (b = 27920,1). Можно составить линей­ную модель, описывающую динамику товарооборота торго­вого предприятия, которая принимает следующий вид:

Y = 27920,1 + 437,425x,

где х = t — порядковый номер месяца.

В нашем примере коэффициент корреляции (см. таблицу 3.12, ячейка Е12) r² = 0,9179, что указывает на высокое качество линейной модели.

В нашем примере F_крит находится по таблице F-распреде­ления на пересечении столбца 1 (так как в модели только од­на переменная х — временной тренд) и строки 14 (см. ячейку F13 таблицы 3.12). В приложении А находим для рас­пределения Фишера с (1;14) степенями свободы, что при 5%-м уровне значимости (доверительная вероятность 95 %) табличное значение F_кp = 4,6. Поскольку F = 156,567 > 4,6 (см. ячейку Е13 таблицы 3.12), то полученная модель трен­да полезна для использования в прогнозировании.

Рассчитаем значения t-статистики для оценки параметров m и b построенной нами модели на основе данных таблицы 3.12:



Табличное значение t_крит для уровня значимости 0,05 (до­верительная вероятность 0,95) с df = 14 степенями свободы равно 2,145 (см. приложение Б). Поскольку |t_m| > 2,145, |t_f| > 2,145, статистическая значимость параметров построенной модели признается весьма высокой.

---

Задание 7. Использование функции ТЕНДЕНЦИЯ для построения прогнозов

Составить прогноз товарооборота торгового пред­приятия по данным таблицы 3.6 с помощью функции ТЕНДЕНЦИЯ.

Выполнение:

Функция ТЕНДЕНЦИЯ рассчитывает прогнозные значе­ния исследуемого показателя в соответствии с линейным трендом. Она с помощью метода наименьших квадратов аппроксимирует прямой линией мас­сивы известных значений у и известных значений х, а также определяет точки, лежащие на этой ли­нии, и прогнозирует значения у для вновь заданных значе­ний х. Но при этом ТЕНДЕНЦИЯ не приводит математичес­кого описания и статистических характеристик самой моде­ли тренда.

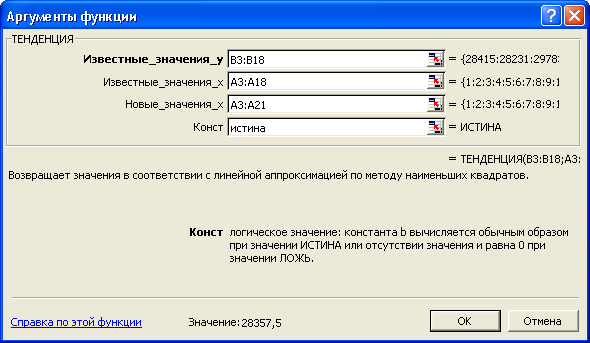
Вызвать функцию ТЕНДЕНЦИЯ можно из окна диалога Мастера функций, расположенного на панели Стандартная, в категориях – Статистические. ТЕНДЕНЦИЯ имеет четыре аргумента (рисунок 3.12):

1) Известные значения у;

2) Известные значения х;

3) Новые значения х;

4) Конст.

Первый, второй и четвертый аргументы формируются аналогично тому, как это происходит при работе с функцией ЛИНЕЙН (соответственно первым, вторым и третьим ее ар­гументом).

Третий аргумент — это определяемые самим пользовате­лем значения х (в модели тренда — времени t), для которых ТЕНДЕНЦИЯ рассчитывает по найденной модели соответст­вующие значения у. Так, при прогнозировании товарооборо­та торгового предприятия с помощью функции ТЕНДЕН­ЦИЯ на рабочем листе выделим диапазон ячеек С3:С21, где ячейки С3:С18 - для отражения значений каждой точки базового интервала вре­мени на линии тренда (таблица 3.14), а ячейки С19:С21 - для перспективной оценки товарооборота на три ближайших месяца. Аргумент Новые значения х в этом случае будет за­дан ячейками А3:А21, и формируется следующая формула массива: =ТЕНДЕНЦИЯ(В3:В18;А3:А18;А3:А21).

По окончании работы с окном диалога ТЕНДЕНЦИЯ необходимо нажать на клавиатуре кнопки Ctrl + Shift + Enter. В выходном диапазоне (см. столбец С таблицы 3.14) фун­кция ТЕНДЕНЦИЯ моментально отразит все рассчитанные на основе линейной модели тренда значения у, соответствую­щие заданному аргументу Новые значения х (т.е. ячейкам А3:А21). Из них значения, находящиеся в ячейках С3:С18, будут относиться к базовому временному интервалу, а в ячейках С19:С21 — содержать прогноз товарооборота на 17-й, 18-й и 19-й месяцы.

---