Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

Рисунок 3.2 - Окно диалога Корреляция
Проведение всех обозначенных действий с данными таблицы 3.4 позволяет получить матрицу значений парных ко­эффициентов корреляции, рассчитанных для всех возмож­ных пар переменных без учета влияния других факторов (таблица 3.5). Поскольку коэффициент корреляции двух набо­ров данных не зависит от последовательности их обработки, то выходная область занимает только половину предназна­ченного для нее места. Ячейки выходного диапазона, имею­щие совпадающие координаты строк и столбцов, содержат значение 1, так как каждая строка или столбец во входном диапазоне полностью коррелирует с самим собой.

Таблица 3.5 - Матрица парных коэффициентов корреляции

	А	В	С	D	E	F
21		Объем товарооборота, ден. ед.	Оборачиваемость товаров, дни	Удельный вес торговой площади в общей, %	Удельный вес торгово-оперативного персонала в общей численности работников, %	Удельный вес товаров с высокими торговыми надбавками, %
22	Объем товарооборота, ден. ед.	1
23	Оборачиваемость товаров, дни	-0,90538094	1
24	Удельный вес торговой площади в общей, %	0,75014268	-0,690531	1
25	Удельный вес торгово-оперативного персонала в общей численности работников, %	0,38663194	-0,153964	0,3726409	1
26	Удельный вес товаров с высокими торговыми надбавками, %	0,50878765	-0,276455	0,0374572	0,580400123	1

---

Вывод: На основе приведенной матрицы можно содержательно оценить связь значений объема товарооборота с каждым из отобранных факторов и выбрать наиболее значимые из них для включения в модель. Так, полученные коэффициенты корреляции, характеризующие тесноту связи объема товаро­оборота с отобранными факторами (см. столбец В21:В26 таблицы 3.5), составляют соответственно: -0,905 для фактора «оборачиваемость товаров»; 0,750 для фактора «удельный вес торговой площади в общей»; 0,509 для фактора «удельный вес товаров с высокими торговыми надбавками»; 0,387 для фактора «удельный вес торгово-оперативного персонала в общей численности работников». Согласно шкале Чеддока (таблица 3.1), для данного торгового предприятия показатель объема товарооборота имеет весьма высокую тесноту связи с фактором «оборачиваемость това­ров» и высокую — с фактором «удельный вес торговой пло­щади в общей». Значение коэффициента корреляции, рассчитанное для товарооборота и фактора «удельный вес торгово-оперативно­го персонала», свидетельствует о слабо выраженной линей­ной связи между этими показателями.

Знак «-» перед коэффициентом корреляции в ячейке В23 означает, что между объемом товарооборота и размером товарооборачиваемости в днях имеет место обратная связь, т.е. при росте количества дней одного оборота товарного запаса предприятия в днях (иными словами — замедлении товарооборачиваемости) объем его реализации при прочих равных условиях будет падать. С остальными факторами объем то­варооборота находится в прямой зависимости.

Задание 3. Прогнозирование развития показателей с помощью линии тренда Excel

Составить прогноз товарооборота торгового пред­приятия на 17-й месяц (см. данные таблицы 3.6) с помощью ко­манды Добавить линию тренда.
Таблица 3.6 - Сведения о динамике товарооборота торгового предприятия

	А	В	С	D	E	F
1
2	Порядковый номер месяца	Объем товарооборота, ден. ед.
3	1	28415
4	2	28231
5	3	29783
6	4	30969
7	5	30494
8	6	29757
9	7	30850
10	8	31325
11	9	31359
12	10	31610
13	11	32366
14	12	33313
15	13	33508
16	14	33374
17	15	34811
18	16	36046
19	Итого

---

---

Выполнение:

Чтобы составить прогноз развития исследуемого показа­теля, используя линии тренда Excel, сначала необходимо с помощью Мастера диаграмм построить диаграмму (График) его дина­мики на основе базовых данных (ячейки В3:В19 таблицы 3.6).

Когда диаграмма построена, необходимо щелкнуть правой клавишей мыши на любой точке графика, чтобы открылось контекстное меню, в котором содержится команда Добавить линию тренда. После ее выбора Excel выведет ок­но диалога Линии тренда, содержащее две основные вкладки: Тип и Параметры.

Вкладка Тип помогает пользователю выбрать тип линии тренда, которая будет аппроксимировать исходные данные. В диалоговом окне предлагается пять типов линий тренда. Для их построения Excel использует модели следующего вида:

- линейную (у = mх + b);

- полиномиальную (у = b + m₁x + m₂x² +...+ m₆х⁶);

- логарифмическую (у = m · lnx + b);

- экспоненциальную (у = m · е^b·x);

- степенную (у = m · х^b).

После задания типа линии тренда выделяют вкладку Па­раметры. Откроется ее окно диалога, в котором пользова­тель определяет следующие важные моменты:

1) количество прогнозируемых периодов и направление прогноза: вперед или назад;

2) когда выбрана линейная, полиномиальная или экспо­ненциальная кривая роста, то в поле Пересечение кривой с осью у в точке 0 задается ее у-пересечение: если данное поле обозначить флажком, то Excel будет искать лучшее уравне­ние кривой, которая на координатной плоскости обязатель­но должна пройти через начало координат;

3) через установку флажка в соответствующих полях ок­на диалога пользователь решает, отражать ли на выходной диаграмме уравнение, на основе которого была построена ли­ния тренда, и размер квадрата коэффициента корреляции r², характеризующий качество аппроксимации.

C помощью ко­манды Добавить линию тренда составим сразу пять различных вариантов прогноза товарооборота торгового пред­приятия на 17-й месяц и при этом по r² оценить общее качество моделей, на основе которых они были полу­чены.

Используя возмож­ности Excel по созданию в ячейках рабочего листа формул, с помощью приведенных на графиках уравнений кривых рос­та рассчитаем значения прогноза товарооборота на 17-й месяц (таблица 3.7).

---

Таблица 3.7 - Прогноз товарооборота на 17-й месяц

Тип модели тренда	Формула расчета прогноза	Прогноз объема товарооборота на 17-й месяц, ден. ед.
Линейная	=437,43*17+27920	35356,3
Логарифмиче­ская	=2429,4*ln(17)+26981	33864,0
Полиноми­альная	=3,9737*17^3-88,245*17^2+925,09*17+27432	1 37178,5
Степенная	=27215*17^0,0774	33887,9
Экспоненци­альная	=28081*е^(0,0138*17)	35490,0

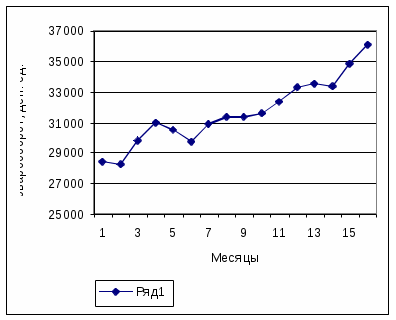Рисунок 3.3 - График развития товарооборота торгового предприятия	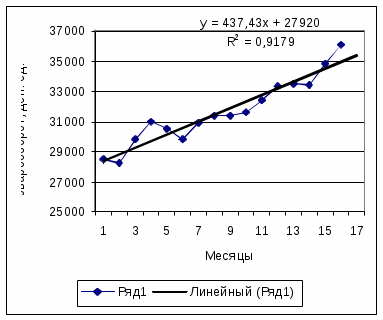Рисунок 3.4 - Оценка прогноза товарооборота торгового предприятия на основе линейной кривой роста
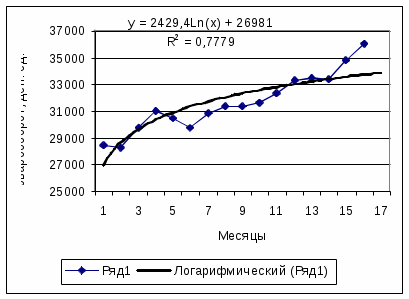Рисунок 3.5 - Оценка прогноза товарооборота на основе логарифмической кривой роста	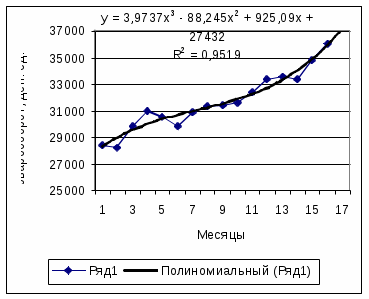Рисунок 3.6 - Оценка прогноза товарооборота на основе полиномиальной кривой роста (степень 3)
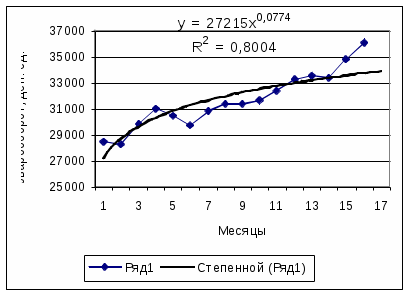Рисунок 3.7 - Оценка прогноза товарооборота на основе степенной кривой роста	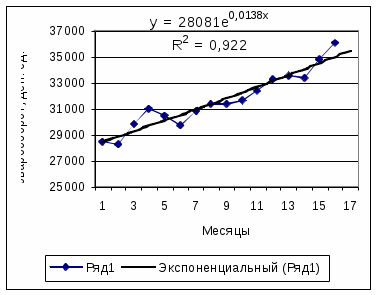Рисунок 3.8 - Оценка прогноза товарооборота на основе экспоненциальной кривой роста

Вывод: Приведенные на рисунках 3.3–3.8 графики динамики то­варооборота свидетельствуют, что наибольшая степень при­ближения линии тренда к базовым данным достигнута в слу­чае полиномиальной кривой роста 3-й степени (см. рисунок 3.6,

---