Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

Задание 10. Составление нелинейных прогнозов с помощью функции РОСТ

Учитывая оценку статистических характеристик фун­кции ЛГРФПРИБЛ, рассчитать прогноз товарооборота по торговому предприятию с помощью функции РОСТ. При этом необходимо получить теорети­ческие значения товарооборота (оцененные на основе най­денной модели у = 28080,897·1,01^х) для базового диапазо­на времени (т.е. 16 прошедших месяцев), а также спрогно­зировать динамику товарооборота на ближайшие 3 месяца.

Выполнение:

Функция РОСТ определяет точки, лежащие на экспоненциальной кривой роста. Она работает точно так же, как ее линейный аналог ТЕНДЕНЦИЯ, и имеет те же четыре аргумента (рисунок 3.15).

Подобно функции ТЕНДЕНЦИЯ, РОСТ вводится как формула массива и требует выделения достаточного числа ячеек для формирования выходного диапазона результатов.

Для формирования выходного массива результатов выде­лим на рабочем листе Excel, соответственно, ячейки С3:С21 (таблица 3.17). Затем вызовем функцию РОСТ из окна диалога Мастера функций. При работе с диалоговым окном РОСТ формула массива принимает вид: =РОСТ(В3:В18;А3:А18;А3:А21). Последнее действие — нажать клавиши Ctrl + Shift + + Enter.

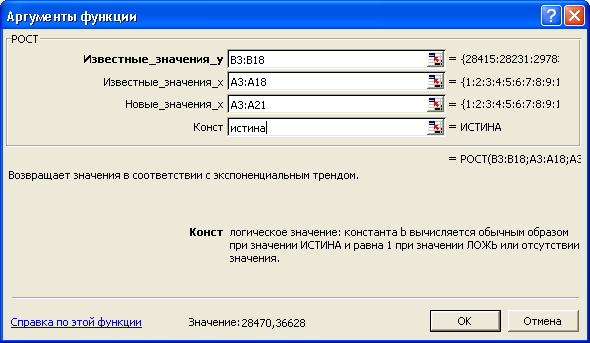
Рисунок 3.15 - Окно диалога функции РОСТ

Таблица 3.17 - Расчет прогноза товарооборота с помощью функции РОСТ

	А	В	С
1
2	Порядковый номер месяца	Объем товарооборота, ден. ед.	РОСТ
3	1	28415	28470,4
4	2	28231	28865,2
5	3	29783	29265,6
6	4	30969	29671,5
7	5	30494	30083,0
8	6	29757	30500,3
9	7	30850	30923,3
10	8	31325	31352,2
11	9	31359	31787,0
12	10	31610	32227,9
13	11	32366	32674,9
14	12	33313	33128,1
15	13	33508	33587,5
16	14	33374	34053,4
17	15	34811	34525,7
18	16	36046	35004,5
19	17		35490,0
20	18		35982,3
21	19		36481,3

---

Задание 11. Прогнозирование с использованием парной регрессии

Проанализировать тесноту связи между товарооборотом торго­вого предприятия и оборачиваемостью товаров и найти уравнение парной регрессии, которое наилучшим образом опишет изучаемую зависимость. Исходные данные представлены в таблице 3.18.
Таблица 3.18 - Исходные данные для поиска уравнения связи переменных

	А	В	С
1
2	Поряд­ковый номер месяца	Объем товаро­оборота, ден. ед.	Обора­чивае­мость товаров, дни
3	1	28415	43,5
4	2	28231	43,0
5	3	29783	43,0
6	4	30969	43,5
7	5	30494	43,0
8	6	29757	42,5
9	7	30850	43,0
10	8	31325	41,5
11	9	31359	42,0
12	10	31610	41,5
13	11	32366	40,5

Продолжение таблицы 3.18

	А	В	С
	Поряд­ковый номер месяца	Объем товаро­оборота, ден. ед.	Обора­чивае­мость товаров, дни
14	12	33313	40,0
15	13	33508	40,0
16	14	33374	39,0
17	15	34811	39,5
18	16	36046	39,0
19

---

Выполнение:

Чтобы найти уравнение парной регрессии, которое наилучшим образом опишет изучаемую зависимость, обратимся к графическому методу. С помощью Мастера диаг­рамм построим точечную диаграмму зависимости товарооборота от оборачиваемости товаров (см. рисунок 3.16).

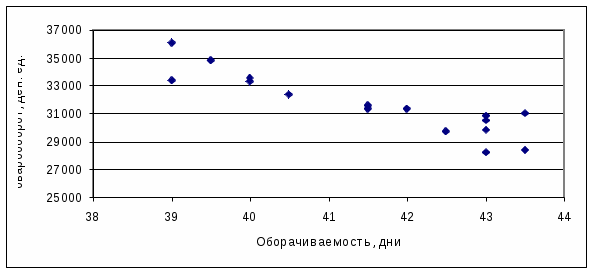
Рисунок 3.16 - График зависимости товарооборота от

товарооборачиваемости товаров
После того как диаграмма построена, необходимо обратиться к команде Excel «Добавить линию тренда» из контекстного ме­ню панели Диаграмма. Учитывая возможности Excel, оце­ним качество аппроксимации базовых данных каждым из пяти предлагаемых окном диалога Линии тренда типом ли­ний: для линейного уравнения R² = 0,8197; для уравнения логарифмической кривой R² = 0,8216; для уравнений полинома 4-й степени R² = 0,8287; для уравнения степенной кривой R² = 0,8155; для уравнения экспоненциальной кривой R² = 0,8142.

Полученные результаты свидетельствуют, что наиболее адекватно (судя по величине R²) отражают зависимость това­рооборота от изменения товарооборачиваемости кривые, пос­троенные на основе уравнений полиномов 4-й степе­ни. На рисунке 3.17 приведена кривая роста, которую описывает уравнение полинома 4-й степени. Рассчитанный Excel коэффициент R² (0,8287) указывает на достаточно высокое качес­тво приближения базовых данных.


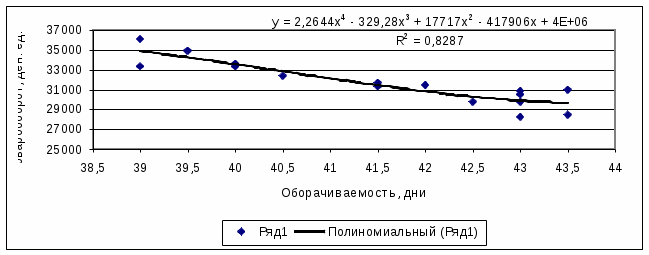
Рисунок 3.17 - Аппроксимация базовых данных полиномиальной кривой роста
Проведем оценку статистической значимости параметров уравнения полинома 4-й степени, построенного на основе соответствующего массива базовых данных (таблица 3.19, ячей­ки A2:F18) с помощью функции ЛИНЕЙН. Для формирования выходного массива значе­ний параметров уравнения и статистических характерис­тик обозначим диапазон ячеек В20:F24.
Таблица 3.19 - Оценка статистической значимости модели регрессии с помощью функции ЛИНЕЙН (уравнение полинома 4-й степени)

	А	В	С	D	E	F
1
2	Порядковый номер месяца	Объем товарооборота, ден. ед.	Оборачиваемость товаров, дни (х)	х^2	х^3	х^4
3	1	28415	43,5	1892,3	82312,9	3580610,1
4	2	28231	43	1849,0	79507,0	3418801,0
5	3	29783	43	1849,0	79507,0	3418801,0
6	4	30969	43,5	1892,3	82312,9	3580610,1
7	5	30494	43	1849,0	79507,0	3418801,0
8	6	29757	42,5	1806,3	76765,6	3262539,1
9	7	30850	43	1849,0	79507,0	3418801,0
10	8	31325	41,5	1722,3	71473,4	2966145,1
11	9	31359	42	1764,0	74088,0	3111696,0
12	10	31610	41,5	1722,3	71473,4	2966145,1
13	11	32366	40,5	1640,3	66430,1	2690420,1
14	12	33313	40	1600,0	64000,0	2560000,0
15	13	33508	40	1600,0	64000,0	2560000,0
16	14	33374	39	1521,0	59319,0	2313441,0
17	15	34811	39,5	1560,3	61629,9	2434380,1
18	16	36046	39	1521,0	59319,0	2313441,0
19	17 (прогноз)	36667	37,5
20		2,269166117	-330,0698403	17765,93	-419248	3693351,7
21	Статистика	100,6502388	16606,9862	1027052	28216610	290563825
22		0,828678371	1050,630858	#Н/Д	#Н/Д	#Н/Д
23		13,30168019	11	#Н/Д	#Н/Д	#Н/Д
24		58730919,23	12142077,21	#Н/Д	#Н/Д	#Н/Д

---

При определении в диалоговом окне ЛИНЕЙН аргумен­тов функции формируется следующая формула массива: =ЛИНЕЙН(В3:В18;С3:F18;ИСТИНА;ИСТИНА).

В первой строке массива результатов, отображенного функцией ЛИНЕЙН после нажатия клавиш Ctrl + Shift + + Enter (ячейки В20:F24 таблицы 3.19), находим уточненные в ходе математических расчетов значения параметров уравне­ния.

Вывод: Модель связи товарооборота (у) и оборачиваемости това­ров (х), построенная на основе уравнения полинома 4-й сте­пени, имеет вид:

у = 3693352 - 419248х + 17765,93х² - 330,07х³ + 2,269х⁴.

Заметьте, что рассчитанный в массиве Статистика ко­эффициент R², равный 0,8287 (ячейка В22), соответствует значению R², приведенному на рисунке 3.17.

В нашем примере (см. таблицу 3.19) значения всех рассчитан­ных параметров уравнения (ячейки В20:F20) меньше по мо­дулю значений их стандартных ошибок (ячейки В21:F21). Следовательно, надежность оценок параметров регрессии не может быть признана удовлетворительной и составленную модель не следует применять для прогнозирования исследуе­мого показателя.

Используя линии тренда Excel, найдем уравнение другой кривой, для которой значение R₂ будет наибольшим. Таким об­разом, наилучшее качество аппроксимации исходных дан­ных достигается в случае уравнения логарифмической кри­вой (рисунок 3.18).

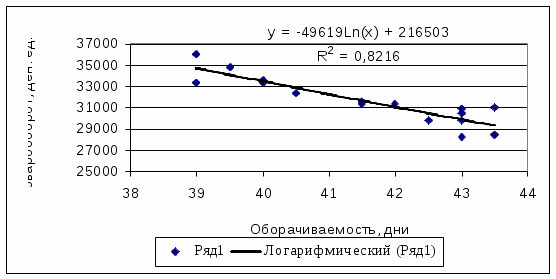
Рисунок 3.18 - Аппроксимация базовых данных логарифмической кривой роста
Статистическую надежность сделанной оценки можно проверить с помощью F-критерия, расчетное значение которого в случае парной регрессии определяют на основе следующей формулы

.

Итак, для уравнения парной регрессии с коэффициентом R², равным 0,8216, F= 64,5.

По таблице F-распределения (см. приложение А) находим, что при 5%-м уровне значимости для распределения Фишера с (1;14) степенями свободы F_крит = 4,60. Поскольку 64,5 > 4,60, можно сделать вывод об адекватности и достаточной точности модели. Следовательно, при условии сохранения существовавшей ранее взаимосвязи переменных на период упреждения модель вида

---

у = -49619ln(х) + 216503 мо­жет быть использована для прогнозирования.

Чтобы составить прогноз объема товарооборота на 17-й месяц, осталось определить значение переменной х (т.е. оборачиваемости товаров) для данного месяца. Это зна­чение может быть получено (в зависимости от характера по­казателя) на основе экстраполяционных методов, методов экспертных оценок или непосредственно задано составите­лем прогноза. Так, будем полагать, что рассматриваемое тор­говое предприятие на 17-й месяц планирует проведение оп­ределенных рекламных мероприятий и выставки-продажи, что по оценкам специалистов позволит ускорить оборачивае­мость товаров в среднем на 1,5 дня. В этом случае товарооборачиваемость по предприятию в прогнозируемом месяце сос­тавит 37,5 дня.

Прогноз объема товарооборота можно получить, создав соответствующую модели формулу в любой (предваритель­но выделенной) ячейке рабочего листа. Выделим, к приме­ру, ячейку В19 (см. таблицу 3.19) и внесем в нее следующую формулу: =-49619*ln(37,5)+216503. После нажатия клавиши Enter в ячейке В19 отразится прогноз объема товарооборота на 17-й месяц, равный 36 667 ден. ед.
Задание 12. Расчет и оценка уравнения множественной регрессии средствами Excel

Построить модель множествен­ной линейной регрессии, которая позволит оценить объем товарооборота на ближайшую перспективу при заданных па­раметрах независимых переменных: «обо­рачиваемость товаров» и «удельный вес товаров с высо­кими торговыми надбавками». Исходные данные представлены в таблице 3.20.
Таблица 3.20 - Исходные данные

	А	В	С	D
1
2	Поряд­ковый номер месяца	Объем товаро­оборота, ден. ед.	Обора­чивае­мость товаров, дни	Удельный вес товаров с высокими торговыми надбавками, %
3	1	28415	43,5	22,5
4	2	28231	43,0	18,0
5	3	29783	43,0	24,9
6	4	30969	43,5	24,4
7	5	30494	43,0	20,6
8	6	29757	42,5	19,0
9	7	30850	43,0	22,2
10	8	31325	41,5	21,6
11	9	31359	42,0	19,8
12	10	31610	41,5	19,7
13	11	32366	40,5	23,1
14	12	33313	40,0	23,9
15	13	33508	40,0	21,2
16	14	33374	39,0	20,4
17	15	34811	39,5	24,2
18	16	36046	39,0	26,5

---