Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

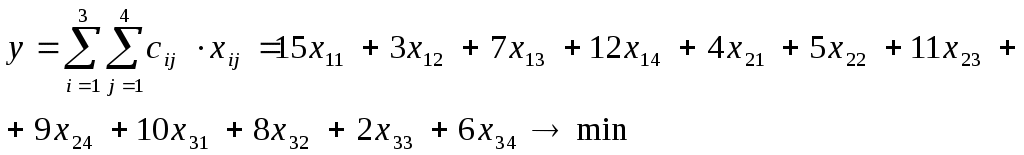
и заявок магазинов:Равенство запасов и заявок соблюдается: Значит, имеем транспортную задачу закрытого типа.Теперь, пользуясь данными исходной таблицы, составим экономико-математическую модель транспортной задачи:найти такие неотрицательные значения: x₁₁, x₁₂ x₁₃ x₁₄ x₂₁ x_22, x₂₃, x₂₄, x₃₁, x₃₂, x₃₃, x₃₄, которые бы давали минимум функции цели: при следующих условиях:- вывоз всех товаров с баз- полное выполнение заказов магазинов- исключение встречных перевозок .В таком виде экономико-математическая постановка задачи считается законченной.2 Решение задачи с помощью инструмента Excel Поиск решенияАлгоритм решения задачи состоит из нескольких этапов:

1. 
   Внести данные по издержкам С_ij в диапазон А1:F6 (таблица 2.2).
   

Таблица 2.2 - Ввод исходных данных

	А	B	C	D	E	F
1	Поставщики	Потребители				Запасы поставщиков
2		В1	В2	В3	В4
3	А1	15	3	7	12	180
4	А2	4	5	11	9	150
5	А3	10	8	2	6	120
6	Заявки потребителей	120	110	80	140	450

---

2) Создать на этом же листе Excel в диапазоне А8:F13 следующую таблицу (таблица 2.3). В качестве исходных значений Xij, i=1,2,3, j=l,2,3,4 в блоке В10:Е12 можно взять нули.Таблица 2.3 - Ввод ограничений

	А	B	C	D	E	F
8	Поставщики	Потребители				Запасы поставщиков
9		В1	В2	В3	В4
10	А1	0	0	0	0	=СУММ(В10:Е10)
11	А2	0	0	0	0	=СУММ(В11:Е11)
12	А3	0	0	0	0	=СУММ(В12:Е12)
13	Заявки потребителей	=СУММ (В10:В12)	=СУММ (С10:С12)	=СУММ (D10:D12)	=СУММ (Е10:Е12)	=СУММПРОИЗВ (В3:Е5;В10:Е12)

Чтобы сформировать формулы суммирования для ограничений, выделить блок B10:F13 (т. е. на 1 строку и на 1 столбец больше блока решений) и выполнить Автосуммирование на панели инструментов. В окаймляющие строку и столбец будут занесены формулы суммиро­вания по столбцам и строкам. Эти формулы и будут использованы для правых частей ограничений по потребителям и поставщикам в соответствии с таблицей 2.3.3) Ввести функцию цели Для этого в ячейку F13 занести формулу =СУММПРОИЗВ(В3:Е5;В10:Е12).4) Выбрать команду Сервис → Поиск решения

---

В окне По­иск решения внести:

• в поле Установить целевую ячейку — ссылку на F13;

• в поле Изменяя ячейки — ссылку на В10:Е12;

• установить переключатель на min;

• чтобы задать ограничения, нажать кнопку Добавить и добавить ограничения:

- по столбцам: В13=В6; С13=С6; D13=D6; E13=E6;

- по строкам: F10=F3; F11=F4; F12=F5;

- граничные: В10:E12>0.

Нажать кнопку ОК, затем — Выполнить. Результаты решения представлены в таблице 2.4.

Таблица 2.4 - Результаты расчета

	А	B		C		D	E	F
8	Поставщики	Потребители						Запасы поставщиков
9		В1	В2		В3		В4
10	А1	0	110		70		0	180
11	А2	120	0		0		30	150
12	А3	0	0		10		110	120
13	Заявки потребителей	120	110		80		140	2250

5) Результат сохранить в виде отчета Результаты.Вывод: Минимальные транспортные издержки по перевозке груза составляют 2250 ден. ед. При этом база А₁ поставляет свой товар в магазины В₂ – 110 т, В₃ – 70 т; база А₂ поставляет товар в магазины В₁ – 120 т, В₄ – 30 т; база А₃ поставляет свой товар в магазины В₃ – 10 т, В₄ – 110 т. Запасы поставщиков полностью распределены, а заявки потребителей удовлетворены в полном объеме.Задачи для самостоятельного решения

---

Задача 1 Четыре овощехранилища каждый день обеспечивают кар­тофелем три магазина. Магазины подали заявки соответственно на 17, 12 и 32 т. Овощехранилища имеют соответственно 20, 20, 15 и 25 т. Тарифы (в д.е. за 1 т) указаны в следующей таблице 2.5.Таблица 2.5 – Исходные данные

Овощехранилища	Магазины
	1	2	3
1 2 3 4	2 3 5 3	7 2 6 4	4 1 2 7

Составьте план перевозок, минимизирующий суммарные транс­портные расходы. Задача 2 На каждом из четырех филиалов производственного объединения могут изготовляться изделия четырех видов. Учи­тывая необходимость углубления специализации, решено, что каждый филиал будет выпускать только один из видов изде­лий. Себестоимость изделий различается по филиалам и опре­деляется следующей матрицей: 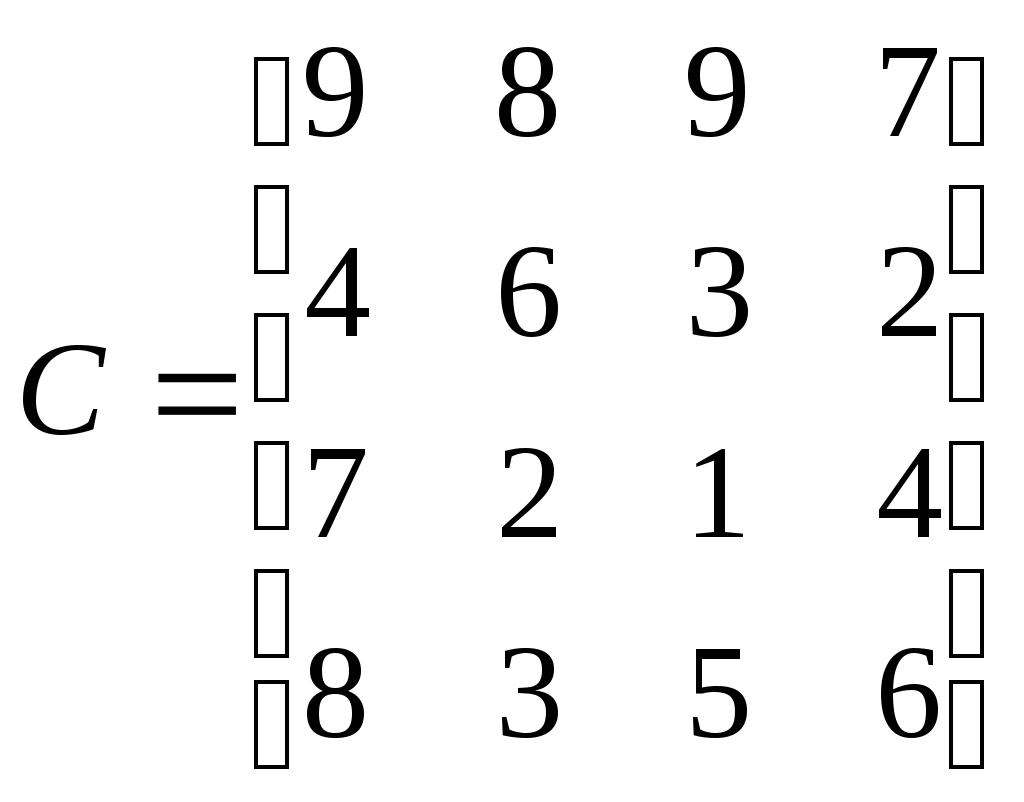.Найти такое распределение выпуска продукции между фи­лиалами, чтобы общая себестоимость продукции была мини­мальной.Задача 3Мясокомбинат имеет в своем составе четыре завода, на каждом из которых могут выпускать три вида колбасных изде­лий. Мощности каждого из заводов соответственно равны 320, 280, 270 и 350 т/сутки. Ежедневные потребности в колбасных изделиях каждого вида также известны и соответственно равны 450, 370 и 400 т. Себестоимость 1 т каждого вида колбасных изделий на каждом заводе определяются матрицей 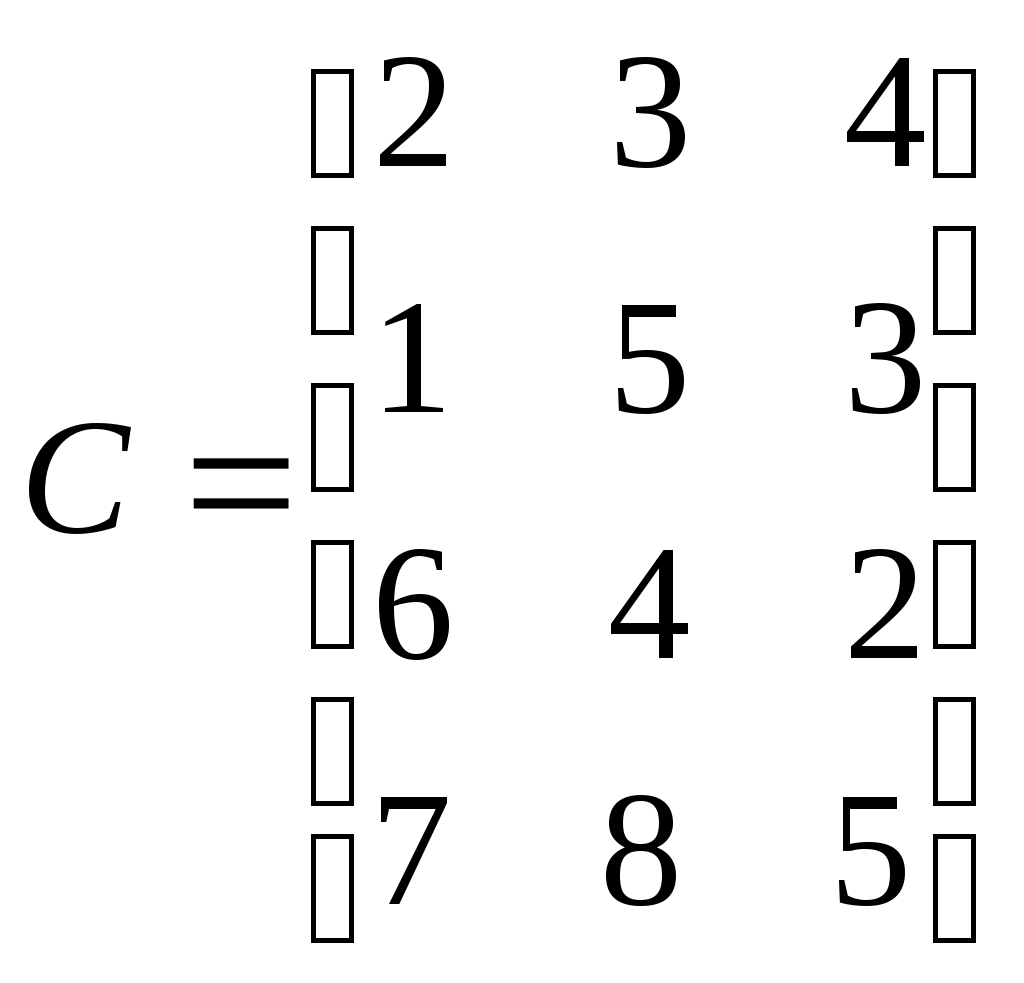.Найти такое распределение выпуска колбасных изделий между заводами, при котором себестоимость изготовляемой продук­ции являлась бы минимальной.Задача 4ОАО «Универмаг «Центральный» получило предложение от фирм ОАО «Элема», ЗАО «Акмо», ОАО «Веснянка» на покупку пальто трех размеров 46-48, 50-52, 54-56. Стоимость пальто в зависимости от размеров и их количественное ограничение даны в таблице 2.6.

---

Таблица 2.6 – Исходные данные

Фирма	Размер			Ресурсы, шт.
	46-48	50-52	54-56
ОАО «Элема»	110	115	126	180
ЗАО «Акмо»	107	115	130	150
ОАО «Веснянка»	104	109	116	120
Потребность, шт.	120	190	140

Определить, как следует распределить заказы для выполнения этих требований, чтобы общая стоимость была минимальной.Задача 5Фирма реализует продукцию в пяти торговых точках. Покупательский спрос жителей этих областей оценивается в соответствующих единицах и задан в таблице 2.7. В этой же таблице представлен профессиональный уровень каждого i-го продавца значениями С_i как доля реализуемых покупательских способностей. Таблица 2.7 – Исходные данные

Объект	I	II	III	IV	V
Спрос	80000	60000	50000	40000	20000
Продавец	1	2	3	4	5
Доля Сi	0,7	0,6	0,5	0,45	0,4

Требуется распределить продавцов по объектам так, чтобы обеспечить максимальную реализацию продукции.

---