Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Так как в формуле (11.15) два неизвестных А=А_бри , то подбор сечения ведут путем последовательных приближений. Задаются , по формуле (11.15) вычисляют площадь сечения А, определяют минимальный радиус сечения i_min , вычисляют гибкость стойки -=l/ i_min , по таблицам=(), путём интерполяции определяют _табл и сравнивают его с избранным. При значительном отличии повторяют попытку, приняв новое значение . И так повторяют попытки до соответствия =_табл . После чего сверяют напряжения [_y]= [_c] c рабочим =F/A. Ошибка по напряжениям не должна превышать 5%.

11.6. Рациальные виды поперечных сечений для сжатых стержней
Если стержень закреплен так, что его приведенная (свободная) длина вобеих главных плоскостях инерции одинаковая, то вычисляя F_кр, необходимо брать наименьший момент инерции. Этот способ закрепления стержня обеспечивает одинаковую форму потери устойчивости в двух главных плоскостях, а рациональным сечением будет такое, у которого главные моменты инерции одинаковы.

Если стержень закреплен так, что его коэффициенты ₁и ₂ , и моменты инерции I₁ и I₂ в обеих главных плоскостях инерции не одинаковы, то необходимо определять две критические силы. Из двух найденных по формуле (11.9) критических сил для расчета принимается наименьшее значение.

Добиваться равноустойчивости стержня можно и за счет различных способов крепления как концов так и пролетов стержня.

Например, если сечение состоит из двух швеллеров (рис. 11.7,а)), то расстояние между их центрами тяжести должно быть определено из условия
I_x=I_y.

Если для одного швеллера моменты инерции I_x1 и I_y1, площадь сечения А₁, то для определения расстояния а можно записать следующее уравнение:

2I_x1=2[I_y1+A₁(a/2)²].

Во всех остальных случаях , например, (рис. 11.7,б)), рациональным будет такое сечение и крепление, при которых равны между собой две критические силы:

---

F_кр1= F_кр2 .

Для этих двух критических сил, получим следующее условие равноустойчивости:


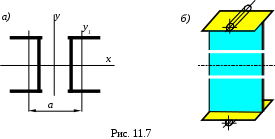
Однако практически при назначении размеров сжатых стержней принимают во внимание целый ряд соображений конструктивного характера (рис. 11.7,б)), поэтому условие равноустойчивости стержня в двух направлениях учитывается по мере возможности.

7. 
   Продольно-поперечный изгиб
   

Если к стержню одновременно приложены сжимающая сила и поперечные нагрузки, то возникает так называемый продольно-поперечный изгиб.

Если стержни обладают малой гибкостью ( 30-40), то при расчете их на прочность и жесткость можно пользоваться принципом независимости действия сил. Такой метод нельзя распространить на гибкие стержни. Расчет гибких стержней, которые работают на сжатие с изгибом, необходимо проводить по так называемой деформированной схеме.

Для случая, показанного на рис. 11.8, изгибающий момент можно определить как сумму двух моментов:

М = М₀+Fv, (11.16)

где М₀– момент только поперечных, определяемый обычным способом.




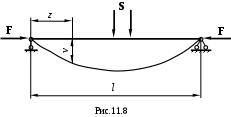
Из выражения (11.16) видно, что суммарный изгибающий момент в сечениях стержня может быть подсчитан только тогда, когда известны перемещения v. Но последние нельзя определить, не зная изгибающих моментов. Таким образом, задача продольно-поперечного изгиба является статически неопределимой задачей.

Для «точного» решения задачи продольно-поперечный изгиба необходимо составить и решить дифференциальное уравнение оси изогнутого бруса

(11.17) Точное решение требует больших преобразований и сложных выводов. Задача особенно усложняется, если нагрузка делит балку на ряд участков, для которых придется писать свои уравнения и проводить их интегрирование.

Рассмотрим приближенный способ определения прогибов при продольно-поперечном изгибе. На рис. 11.9 показана балка на двух шарнирных опорах с произвольной нагрузкой S, сжатой силойF. Прогиб от такой загрузки можно представить в виде суммы двух прогибов:

---

(11.18)

г
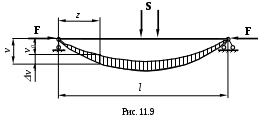
де ₀ - прогиб, вызываемый действием только поперечной нагрузки S без учета силы F;

 - дополнительный прогиб, появившийся в результате действия сжимающей силы F.
Если в дифференциальное уравнение (11.17) подставить выражение (11.18), то получим

(11.19)

Для определения прогибов только от поперечной нагрузки, можно написать следующее уравнение

(11.20)

Поэтому из уравнения (11.19) с учетом (11.20) получим

(11.21) Сделаем предположение, что дополнительные прогибы заштрихованные на рис. 11.9 изменяются по закону синуса (в этом и заключается приближенность решения):



Тогда



Поставляя полученное выражение в уравнение (11.21), имеем



или согласно равенству (11.18)



откуда



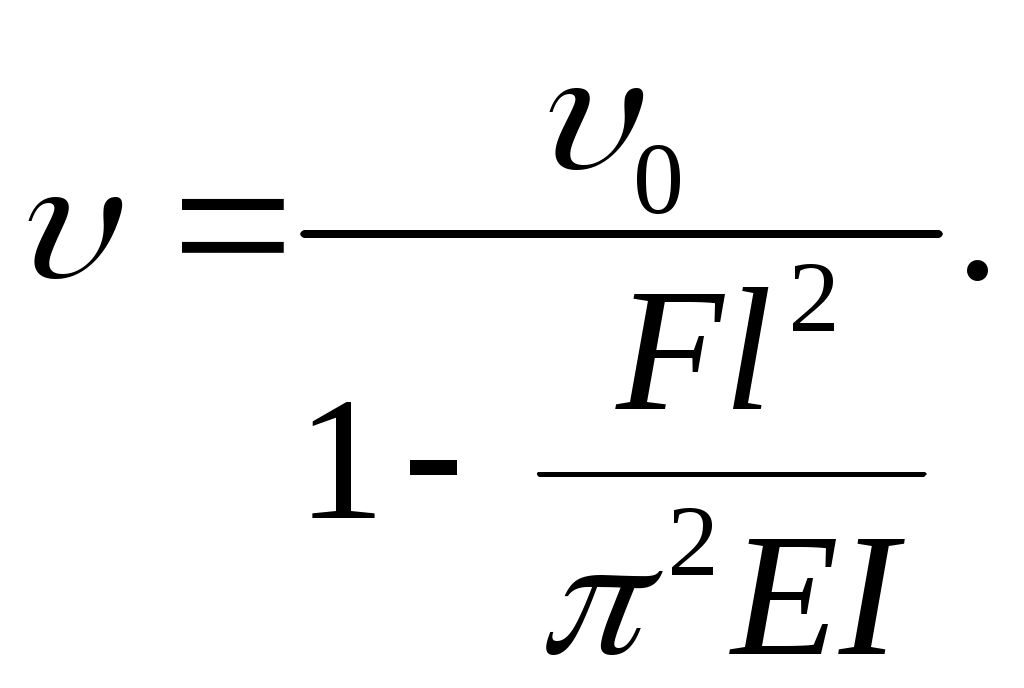
Учитывая, что для рассматриваемого случая величина представляет собой выражение эйлеровой критической силы, окончательно получим

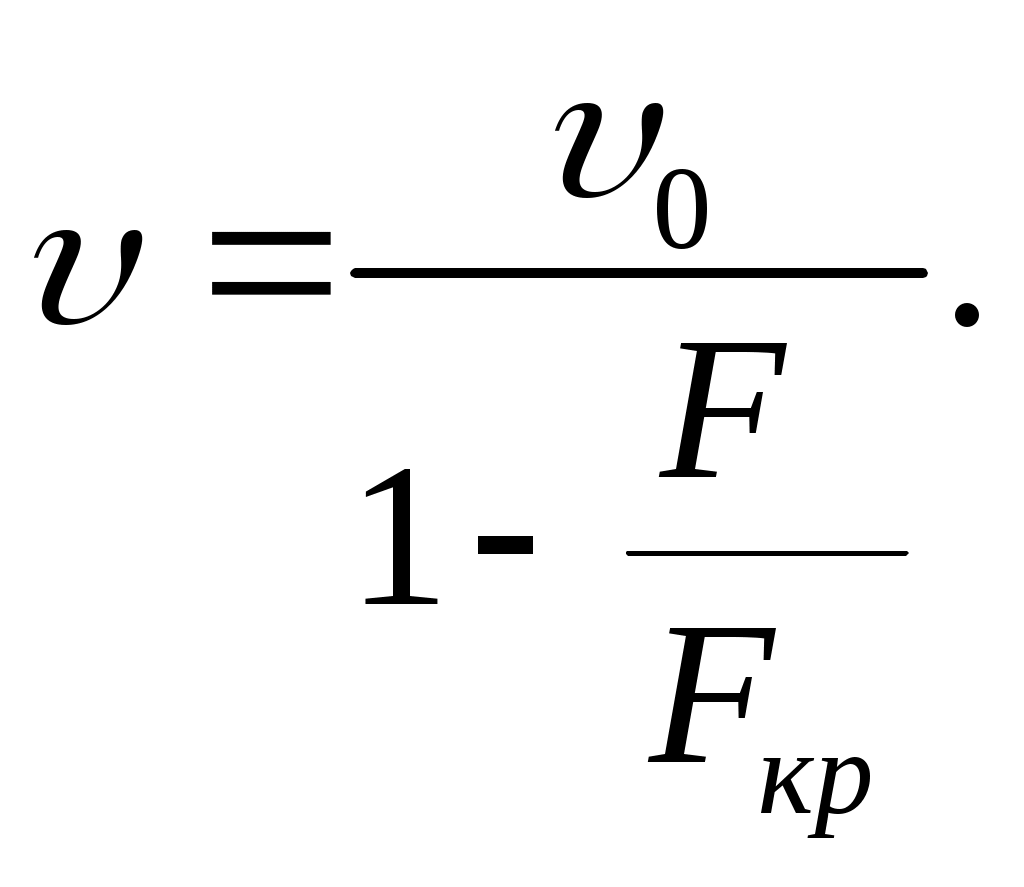(11.22)

Эту формулу можно применять и для других способов крепления концов стержня, при этом F_кр необходимо определять каждый раз с учетом характера закрепления стержня по общей формуле



где I- момент инерции, соответствующий изгибу в данной плоскости.

Величина ₀может быть определена любым известным методом.

---

Формулой (11.22) нельзя пользоваться в тех случаях, когда сжимающая сила F будет близка к критической силе, она должна лежать в интервале

0F0,8F_кр .

В инженерной практике обычно F (0,5 – 0,6)F_кр , поэтому приведенное выше приближенное решение будет достаточным для практических целей.
Наибольшие (сжимающие) напряжения определяются равенством

(11.23)

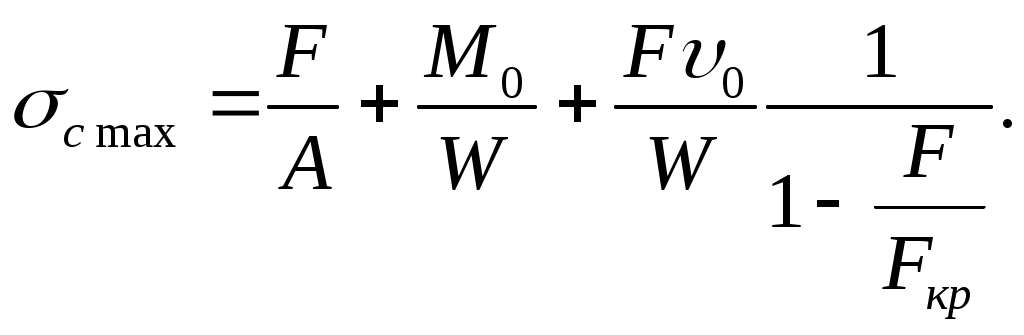
Для сжатого стержня, имеющего малую начальную кривизну, приведенные формулы остаются в силе, при этом под ₀ следует понимать начальный прогиб, обусловленный (начальной) кривизной стержня. Из формулы видно, что зависимость между напряжениями и нагрузками нелинейная, напряжения возрастают быстрее нагрузки. Поэтому расчет на прочность при продольно- поперечном изгибе нельзя вести по допускаемым напряжениям. При проверочном расчете на прочность определяют коэффициент запаса (n), который сопоставляют с требуемым коэффициентом запаса прочности [n].

Величина (n) может быть определена из формулы

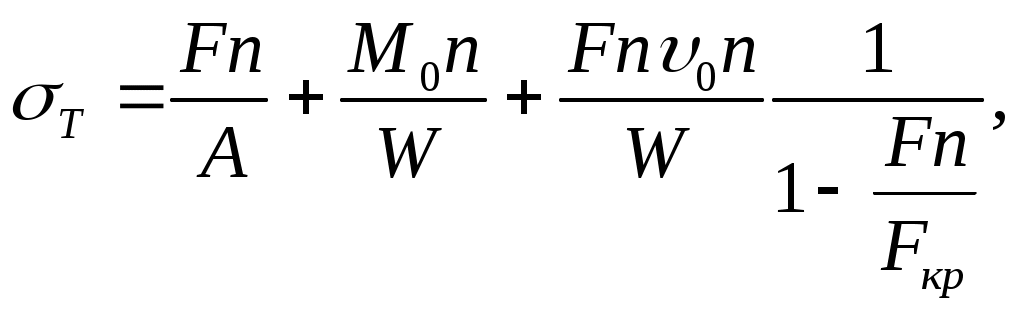(11.24)

где n – число, показывающее, во сколько раз должны возрасти внешние силы, чтобы напряжение в опасной точке стало равным пределу текучести _Т.



11.8. Энергетический метод определения критической силы
Мы ознакомились с методом Л.Эйлера для определения критической силы при сжатии стержня. Однако в задачах с распределенной и сосредоточенными нагрузками, в стержнях переменного сечения для определения критической силы применяют приближенные методы, один из них энергетический.

Метод основан на теореме Лагранжа-Дирихле: если в положении равновесия системы потенциальная энергия имеет минимум, то положение равновесия устойчиво.

Полная потенциальная энергия может быть подразделена на две части, одна из которых соответствует энергии деформации тела, другая определяется потенциальной энергией массовых сил и приложенных поверхностных сил:

П=U-A, (11.25)

где П- полная потенциальная энергия;

U-

---

энергия деформации;

А- работа внешних сил, она противоположна по знаку их потенциальной энергии.

При потере устойчивости происходит изменение энергии упругой деформации (U), а внешние силы при этом совершают работу ( А), при этом полная потенциальная энергия получит приращение ( П):

П=U-A. (11.26)

Если U>A, система будет устойчива, т.е. F<F_кр .

Если U<A, система не устойчива, т.е. F>F_кр .

Если U=A, состояние безразличное, т.е. F=F_{кр ,}

Следовательно, стержень может прогнуться, а может быть и прямолинейным.

Таким образом, F_кр можно получить из условия U=A, что соответствует теореме Лагранжа-Дирихле.
Пример1. Рассмотрим сжатый шарнирно-опертый стержень (рис. 11.10 ). Определим F_кр.





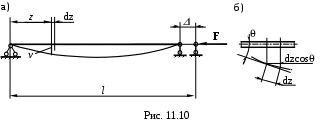
1. Энергия деформации. При изгибе увеличивается потенциальная энергия упругой деформации и которая определяется по формуле

или (11.27)

где v^’’- вторая производная от задаваемого уравнения упругой линии изогнутой оси стержня, которое должно удовлетворять граничным условиям (Г.У.);

EI_X–жесткость поперечного сечения при изгибе.
2. Работа сжимающей силы.

(11.28)

где

(11.29)

Учитывая, что U=A, получим

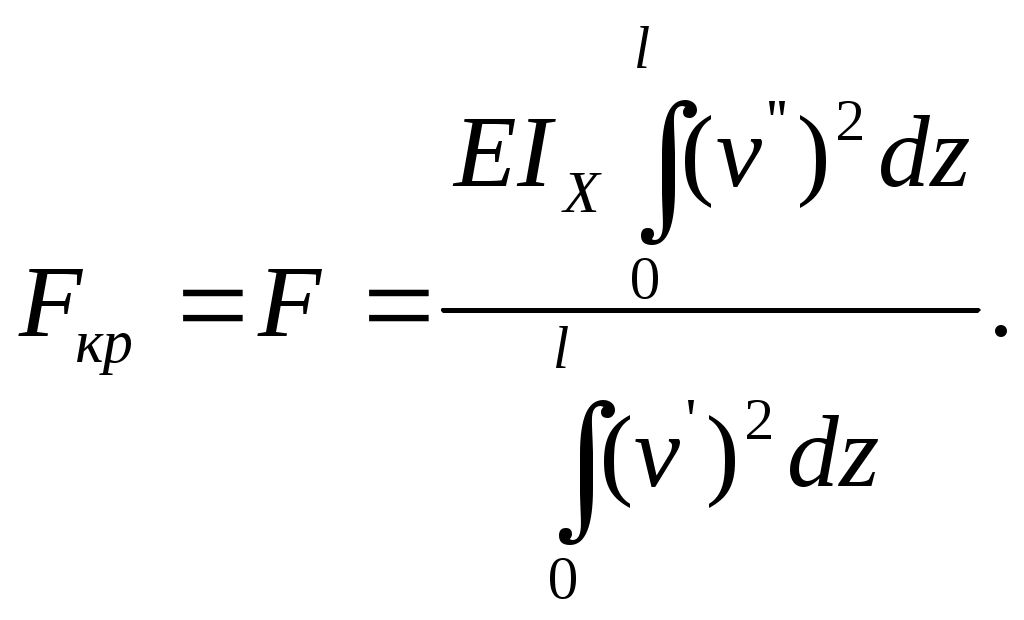(11.30)

Как видим из формулы (11.30), величина F_кр зависит только от формы изогнутой оси стержня ( от функции v= v(z)) и не зависит от “истории” нагружения стержня.

Функцию прогибов v= v(z) необходимо выбирать, соблюдая: граничные условия, условия экстремальных прогибов и точек её перегиба.

Пример 2. Для шарнирно закрепленного стержня (см. рис. 11.10 ) мы знаем функцию прогибов

---