Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

(10.26)

Эта формула является приближенной, учитывающей только напряжения от кручения.

Из уравнения следует, что с увеличением диаметра D пружины прочность её уменьшается и, наоборот, с увеличением диаметра d сечения прочность увеличивается.

10.5.2 Расчёт пружин на жесткость

Под действием сил F, приложенных в крайних сечениях пружины и действующих по оси пружины, последняя будет деформироваться. Изменения длины пружины будем называть осадкой пружины и обозначать через 

(рис. 10.17,а)).

Формулу для подсчёта осадки пружины получим, воспользовавшись интегралом Мора, учитывая только крутящий момент,





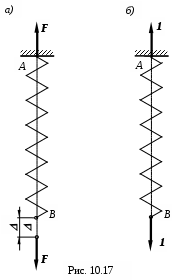
где dz –длина элемента пружины.

Имеем (см. рис. 10.17,а) и б))



а длина всей пружины, измеренная по оси прутка, из которого изготовлена пружина



где n – число витков пружины.

После подстановок получим:



Проведя интегрирование и заменяя I_Р через диаметр d, получим после преобразований формулу для расчёта цилиндрической пружины на жесткость в таком виде

(10.27)

Из формулы (10.27) следует, что чем больше диаметр пружины D и число витков n, тем больше осадка пружины; чем больше диаметр d сечения пружины, тем осадка пружины меньше.

Вопросы для самопроверки

1. 
   Какой случай нагружения бруса называется сложным сопротивлением?
   
2. 
   Какой случай изгиба называется плоским, а какой косым изгибом?
   
3. 
   Каково взаимное расположение силовой линии и нейтральной оси при косом изгибе? Где находятся опасные точки при косом изгибе?
   
4. 
   Когда возникает внецентренное сжатие и растяжение?
   
5. 
   Как располагается (в осях координат) нейтральная линия по отношению к силовой точке? Что такое ядро сечения?
   
6. 
   Как находится опасное сечение вала, работающего на изгиб и кручение?
   
7. 
   Какие точки сечений витков пружины получают набольшие напряжения?
   

---

11. Устойчивость сжатых стержней

11.1. Основные понятия

И
з теоретической механики известно, что равновесие твёрдых тел может быть устойчивым и неустойчивым. Например, шарик, на дне вогнутой сферы, находится в устойчивом состоянии (рис. 11. 1, а)), а на вершине выпуклой сферы – в неустойчивом (рис. 11. 1, б)).




Прямолинейная форма равновесия центрально сжатого стержня при определённой малой нагрузке (F_кр) считается устойчивой, если стержень нечувствителен к малым возмущениям. При нарастании нагрузки (F>F_кр) стержень может оказаться в неустойчивой состоянии, и тогда незначительные случайные воздействия вызовут (искривление стержня) большие отклонения. Стержень, после устранения возмущений (воздействия), останется в изогнутом состоянии под действием продольной силы.

Такое состояние называется продольным изгибом.

До потери устойчивости во всех сечениях стержня наблюдается только центральное сжатие. В момент потери устойчивости к центральному сжатию присоединяется изгиб. Стержень переходит из одного состояния равновесия (устойчивого) в другое (неустойчивое) (рис. 11.2). Т.е. при (F>F_кр) теоретически возможно существование двух форм равновесия. Происходит разветвление форм равновесия. По этому практически малейшее отклонение от прямолинейной формы будем считать потерей устойчивости.

---

Нагрузка, при которой прямолинейная форма перестаёт быть формой устойчивого равновесия, называется критической(F_кр ).

Таким образом, исследование устойчивости стержня заключается в определении F_кр. Для обеспечения устойчивости допускаются нагрузки, составляющие лишь часть критических. Отношение критической нагрузки F_кр к её допускаемой величине ([F]_y) называется коэффициентом устойчивости:

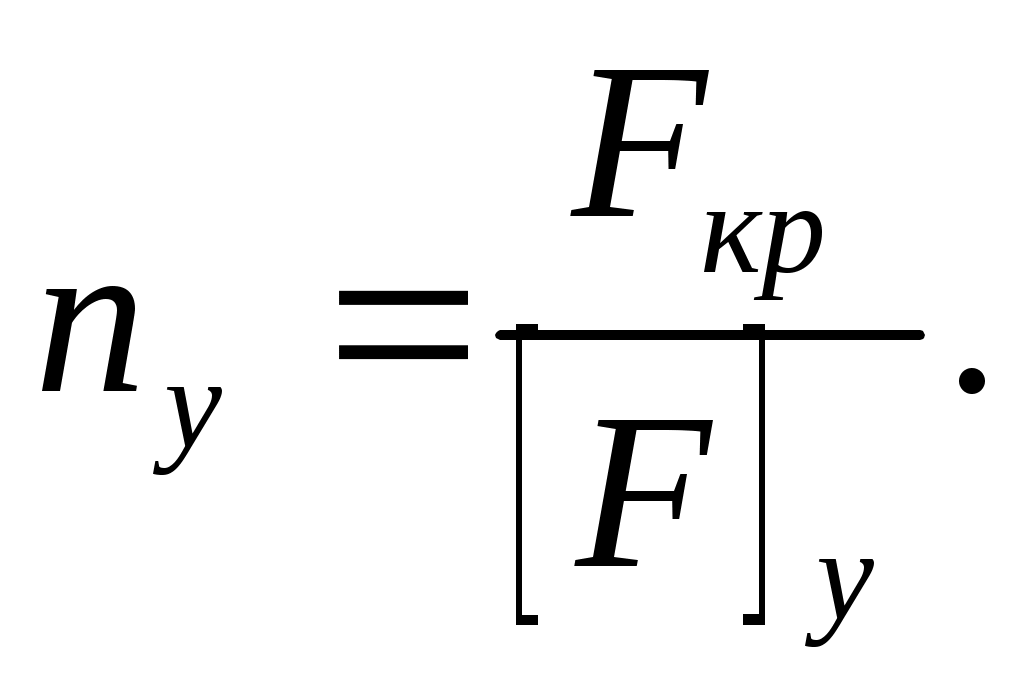(11.1)

Коэффициент n_y зависит от материала стержня. Его рекомендуемые величины находятся в пределах: для стальных стоек 1.5…3; для деревянных 2.5…3.5; для чугунных 4.5…5.5.

2. 
   Метод Эйлера для определения критической силы.
   

Формула Эйлера.
Для исследования устойчивости равновесия упругих систем имеется несколько методов: метод малых колебаний, энергетический метод и др. В инженерной практике для невесомых стержней с нагрузкой, приложенной точно в центре тяжести торцовых сечений и параллельно продольной оси стержня используют более простой метод – метод Эйлера.
Метод Эйлера основан на анализе разветвления форм равновесия упругой системы. Следовательно, при критической силе наряду с исходной прямолинейной формой как бы возможна смежная, весьма близкая к ней искривленная форма.
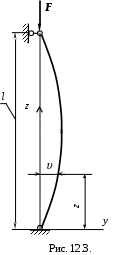Для вывода формулы Эйлера рассмотрим шарнирно - опёртый, центрально - сжатый стержень постоянного сечения (рис. 11. 3) в слегка отклонённом состоянии от прямолинейной формы.

Изгибающий момент в произвольном сечении равен

F (11.2)

Дифференциальное уравнение изгиба стержня запишется в виде:
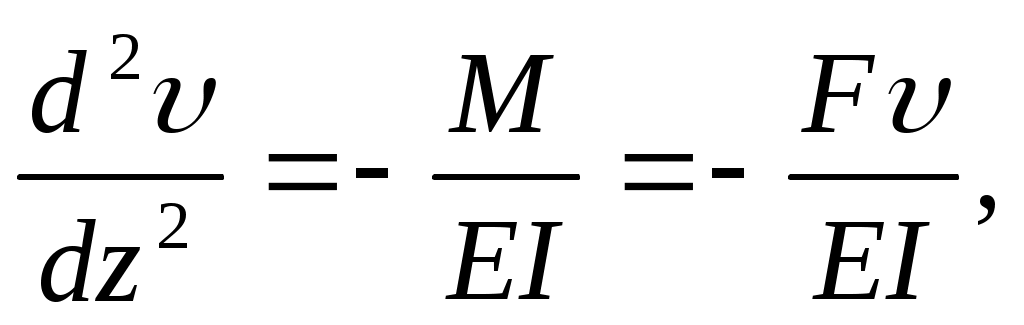(11.3)
или

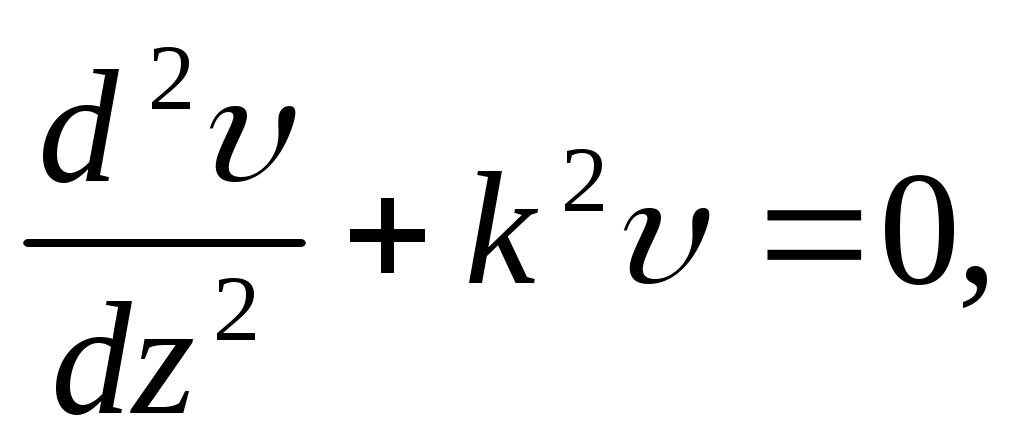(11.4)

где

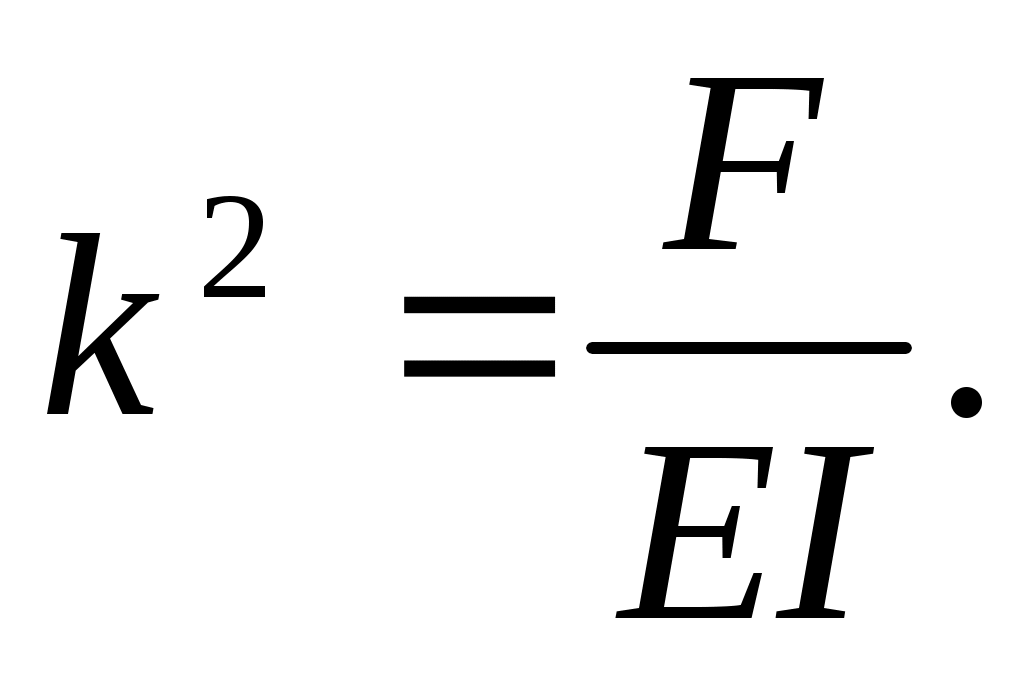(11.5)

Интеграл дифференциального уравнения (11.4) имеет вид
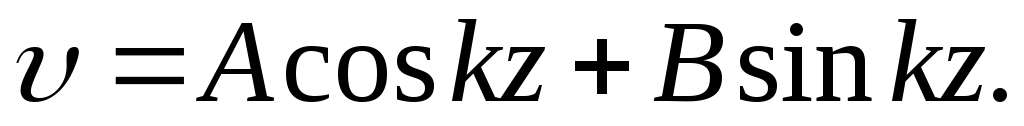(11.6)

Для определения значений произвольных постоянных А и В используем граничные условия. Первое граничное условие: при z=0 и 

Следовательно, уравнение оси изогнутого бруса (6) примет вид

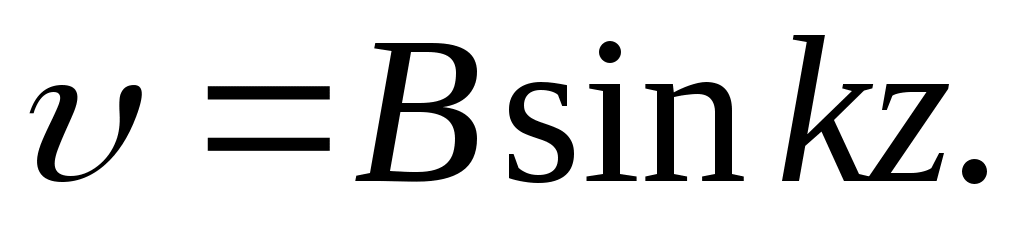(11.7)

Таким образом, стержень изгибается по синусоиде.

Второе граничное условие: при z=l и  Bsinkl=0Это условие выполняется в двух случаях:

1) В=0; 2) sinkl=0

Первый случай нас не интересует, так как при В=0 прогибы во всех точках равны нулю, следовательно, стержень остается прямым.

Второе условие sinkl=0 дает kl= 2 3 nучтя значение k (11.5), получим:



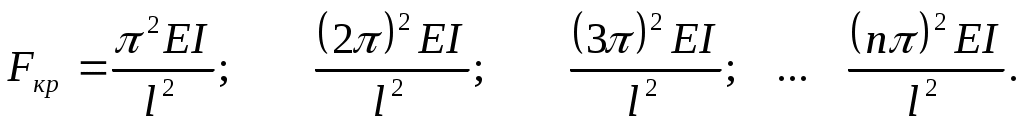
Итак, получено не одно, а множество значений критической силы. Каждой критической силе соответствует своя форма равновесия (рис. 11.4). Подставляя найденное значение k в уравнение оси изогнутого бруса (11.7), замечаем, что при первой критической силе стержень изгибается по одной полуволне синусоиды, а при всех последующих число полуволн равно номеру соответствующей критической силы.







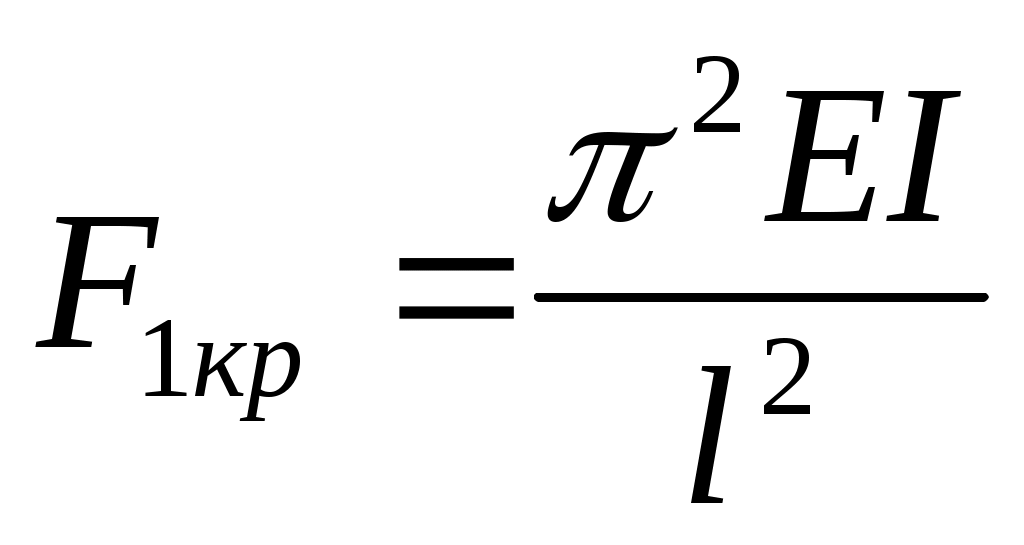
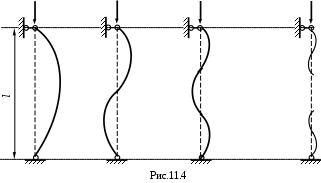
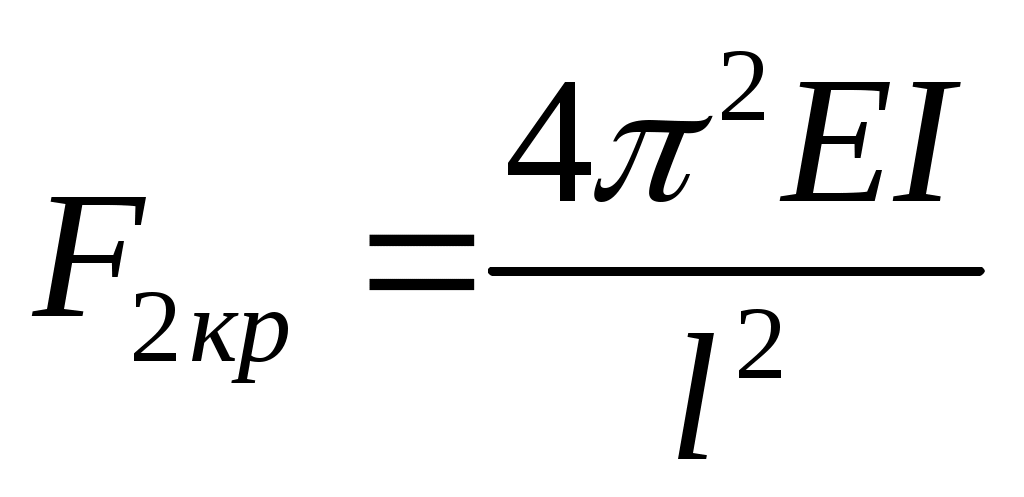
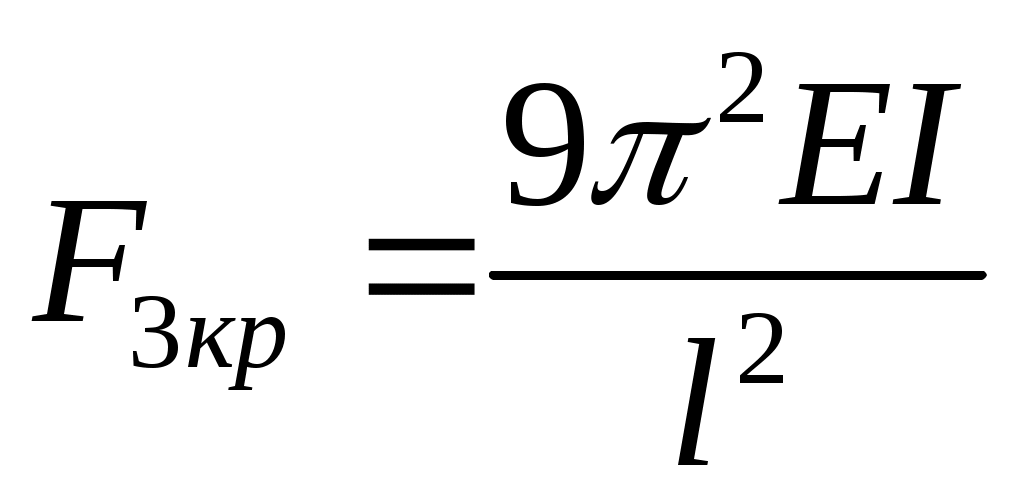
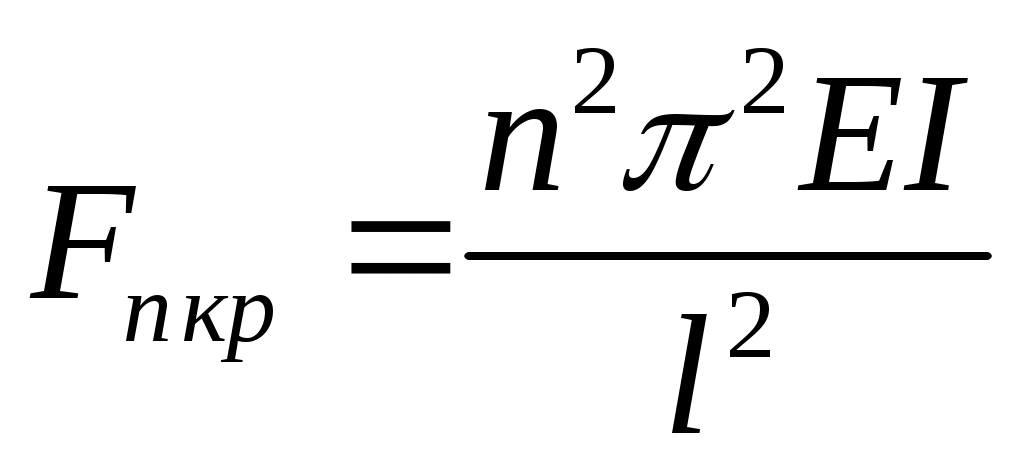
Равновесие, соответствующее первой форме изгиба, является устойчивым, а все всем остальным – неустойчивым.

Для инженерных расчетов практический интерес представляет только наименьшая критическая сила

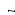
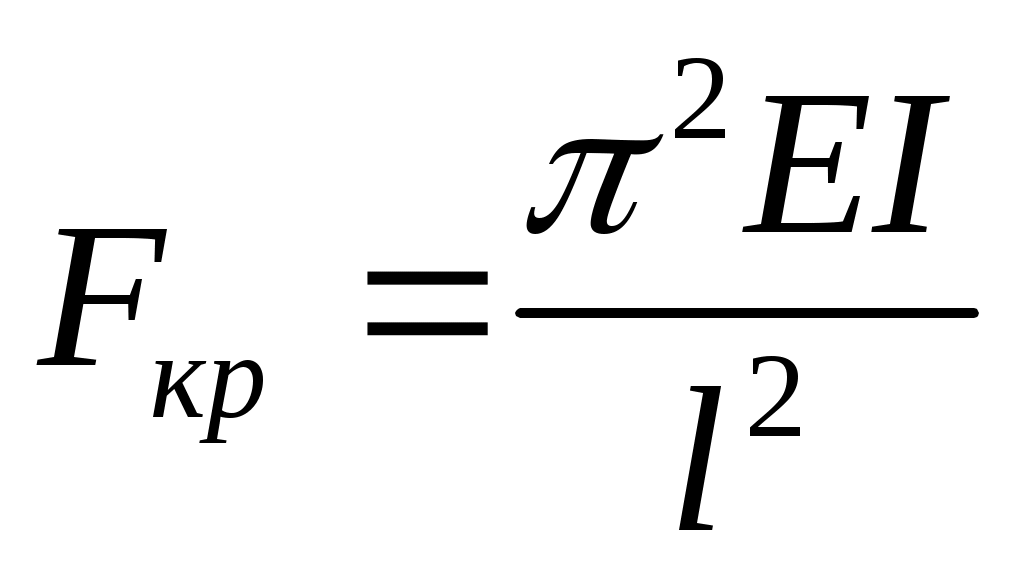(11.8)

Эту формулу в 1744 г. впервые получил Леонард Эйлер, поэтому она называется формулой Эйлера, а определяемую этой формулой критическую силу – эйлеровой силой.

Из формулы (11.8) видно, что величина критической силы прямо пропорциональна жесткости и обратно пропорциональна квадрату длины стержня.

Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости материала, но совершенно не зависит от прочностных характеристик материала, из которого изготовлен стержень. Два стержня с одинаковыми геометрическими размерами, но изготовленные из различных сталей и работающие в упругой стадии, теряют устойчивость при одной и той же критической силе.

Таким образом, выясняется резкая разница между работой стержня на растяжение и на сжатие. Предельная растягивающая сила непосредственно зависит от прочностных характеристик материала и поэтому различна для разных сортов стали, в то время как при сжатии в пределах упругости наблюдается совершенно иная картина.

Предельная растягивающая сила не зависит от длины стержня, в то время как при сжатии она быстро падает с увеличением длины.

Продольный изгиб сжатых стержней особенно опасен потому, что он наступает внезапно, и поэтому его трудно предупредить. В растянутых стержнях признаки опасного состояния часто наступают задолго до разрушения, а в сжатых стержнях каких- либо заметных признаков потери устойчивости, как правило, установить не удается.


11.3. Влияние способов закрепления концов стержня на величину

критической силы

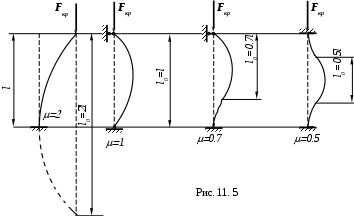
На рис. 11.5 показаны различные случаи закрепления концов сжатого стержня. Для каждого случая необходимо проводить свое решение аналогичное тому, что сделано в предыдущем параграфе для шарнирно опертого стержня. Эти решения показывают, что для всех случаев, изображенных на рис. 11.5, критическую силу можно представить в виде формулы:

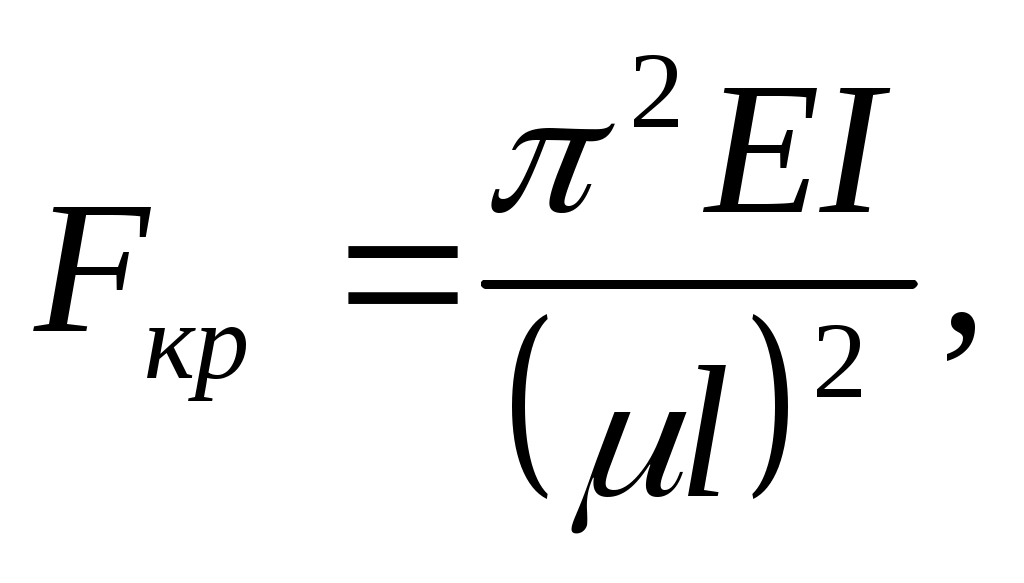(11.9)

где   коэффициент приведения длины, а величина ll₀называется приведенной (свободной) длиной. Понятие о приведенной длине было впервые введено профессором Петербургского института путей сообщения Ф.С. Ясинским (1892).

Свободная длина l₀может быть истолкована как некоторая условная длина шарнирно опертого стержня, имеющего такую же критическую силу, как заданный стержень. В отдельных случаях это положение вытекает из чисто геометрического толкования (длина полуволны синусоды). Так, например, если стержень заделан одним концом, рассматривать как половину стержня, шарнирно опертого по концам, то l₀= 2l. Следовательно, =2.

Для стержня, заделанного двумя концами, длина полуволны, замеренная между двумя точками перегиба, где М_х=0,составит половину длины стержня, следовательно, для этого случая =0,5.



11.4. Пределы применимости формулы Эйлера. Формула Ясинского
Формула Эйлера, полученная более 267 лет назад, долгое время являлась предметом дискуссий. Формула Эйлера для некоторых случаев не подтверждалась экспериментами. Объясняется это тем, что формула Эйлера выводилась в предположении, что при любом значении силы стержень работает в пределах упругих деформаций с использованием закона Гука. По этому формулу Эйлера нельзя применять в случаях, когда критические напряжения больше предела пропорциональности. Для установления предела применимости формулы Эйлера найдем



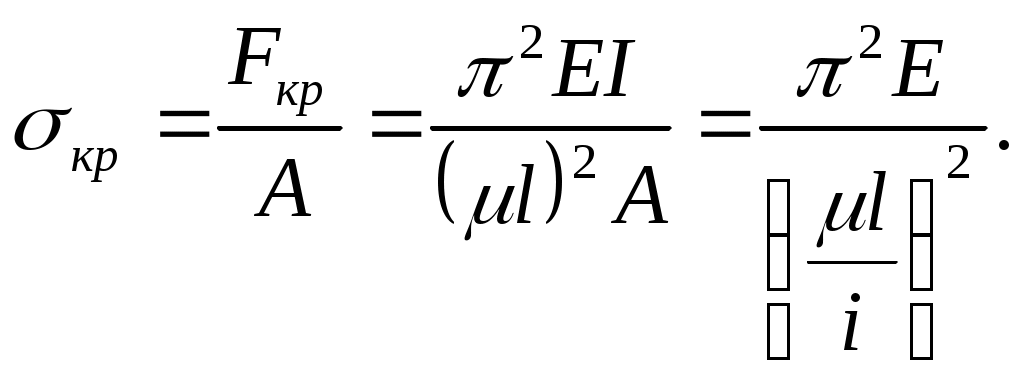
Здесь 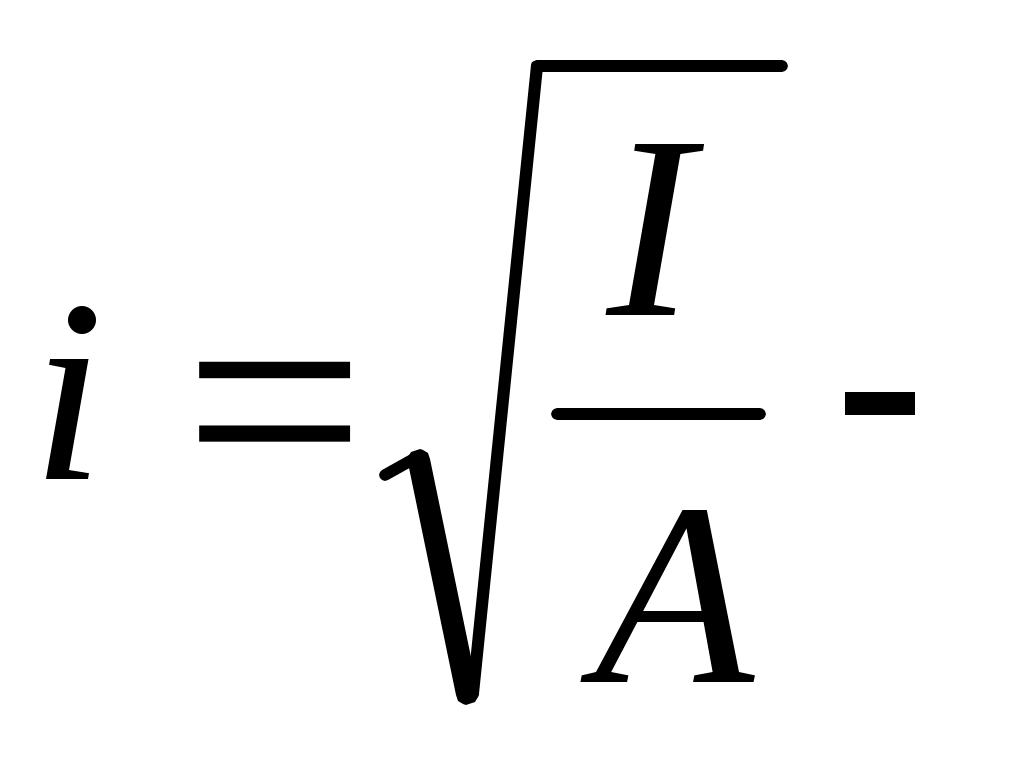радиус инерции.




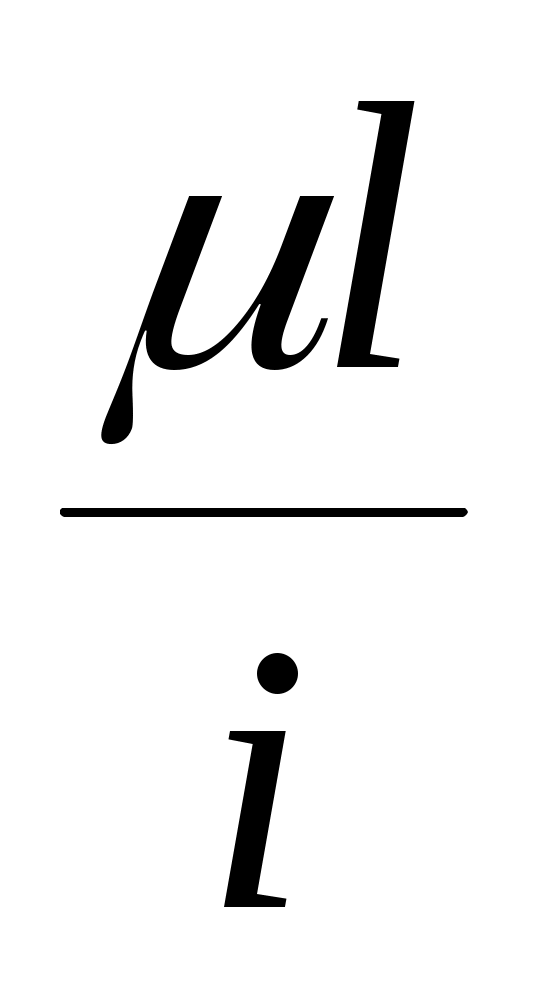
Обозначим через  Величина  называется гибкостью стержня.

Итак,

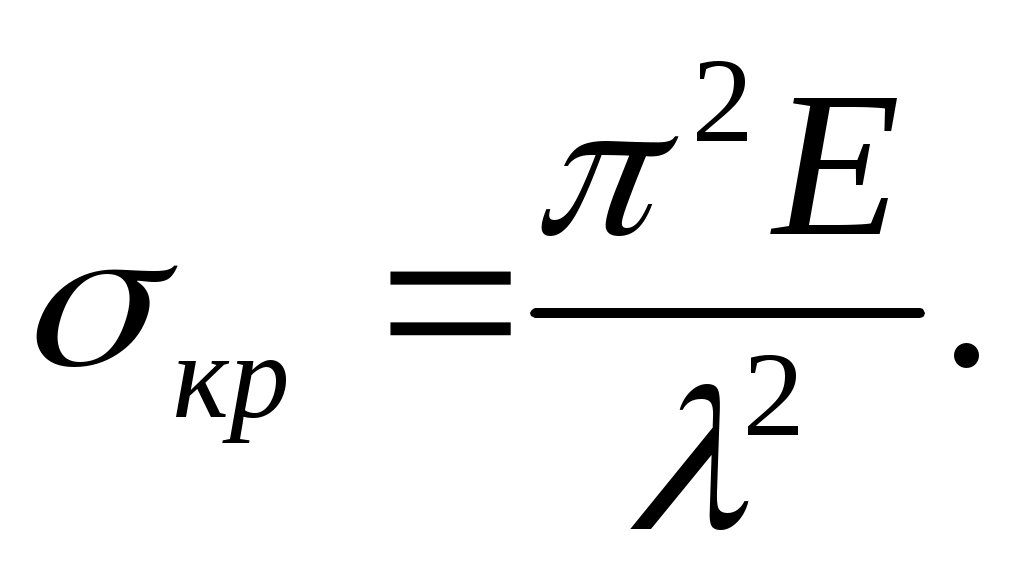(11.10)

Это так же формула Эйлера, но записанная для критического напряжения, а не для критической силы.

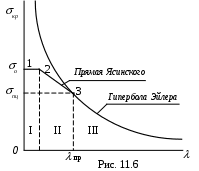
Принято изображать уравнение (11.10) в координатах _кр -(рис. 11.6).

Полученную кривую часто называют гиперболой Эйлера.

Как видно из уравнения (11.10), при малых гибкостях критические напряжения могут значительно превосходить предел прочности материала. Действительно короткие и толстые стержни (например, кубы, имеющие гибкость  3.5) разрушаются от сжатия при достижении напряжением предела текучести (пластичные материалы(

---

₀ = _Т ), либо предела прочности (хрупкие материалы(₀ = _пч)).

Отсюда ясно, что при малых гибкостях формула Эйлера непригодна, причиной является превышение критическим напряжением предела пропорциональности.

Поэтому ордината (_пц) рассечет гиперболу Эйлера на две части, из которых нижняя (большие гибкости _пр) пригодна, а верхняя (малые гибкости _пр) должна быть отброшена.

Приравнивая напряжение _кр пределу пропорциональности _пц, получим предельное значение гибкости

(11.11)

Если _пр, то можно применять формулу Эйлера. Если _пр, то формулой Эйлера ползоваться нельзя.

Для стали Ст. 3 _пц  200МПа, Е=200ГПа, получим _пр100.

Д ля серого чугуна _пр  80; для дерева хвойной породы_пр 110 и т. д. Для случая, когда стержень работает за пределами упругих деформаций, теоретические выводы сильно усложняются. Поэтому были проведены экспериментальные исследования. К числу таких исследований прежде всего необходимо отнести работу Ф.С. Ясинского.

Оказалось целесообразно разделить стержни по их гибкости на три группы (рис. 11.6.):

жёсткие (малой гибкости ₁<3040 ); средней гибкости (₁<_пр ) и большой гибкости (гибкие), для которых _при пригодна формула Эйлера.

Для стержней I^ой- группы, когда короткий стержень (₁<30 40 ) практически разрушается при потере прочности, расчёт ведётся на простое сжатие здесь допустимо _кр=_о=const.

Для стержней II^ой- группы ,когда (₁<_пр ) расчёт ведётся на устойчивость за пределом пропорциональности, а зависимость между _кр и  принимает на основе опытных данных Ф.С. Ясинского либо линейный _кр=a-b, либо степенной

_кр=a-b+с², ( 11.12)

где a, bи

---

c – постоянные, зависящие от материала.

Так, например, для стали Ст.3 а=310; b=1.14; для дерева a=29.3; b=0.194; для чугуна a=776; b=12; c=0.05.

Для стержней III^ей- группы,когда (_пр ) применяется формула

Эйлера ( 11.9).


11.5. Практический расчет сжатых стержней

При назначении размеров сжатых стержней в первую очередь заботятся о том, чтобы стержень при действии сжимающих сил не потерял устойчивость. Поэтому напряжения в сжатом стержне должны быть обязательно меньше критических:
( 11.13)

Здесь N =F - сила, на которую рассчитывается стержень;

F_кр – критическая сила;

А_brutto = А - площадь сечения.

Исследования показали, что местные ослабления, например, заклепочные отверстия, ослабления за счет врубок и т.п., не оказывают существенного влияния на величину критической силы. Этим объясняется, что в формуле (11.13) при определении критических напряжений часто берется площадь сечения брутто.

Для надежной работы сжатого стержня необходимо предусмотреть определенный запас устойчивости.
N =

Деля левую и правую части неравенства на А - площадь сечения, приходим к неравенству



Обозначив _кр n_y=[_y] получим формулу
.

Следовательно, [_y] на устойчивость можно сопоставить с [_с] при расчете на простое сжатие и получить коэффициент уменьшения основного допускаемого напряжения при продольном изгибе  .

[_y] [_с] (11.14)

Коэффициент  зависит от критического напряжения, а следовательно, является функцией гибкости стержня .Значения величины коэффициента  для различных гибкостей установлены нормами и обычно приводятся в виде таблиц.
Тогда с учетом последнего имеем

(11.15)
По этой формуле можно определить допускаемое продольное усилие и подобрать сечение.

---