Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 402
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
АВ, не проходящей через центр тяжести сечения. Для двух крайних случаев, когда сила приложена в точках А и В, нулевые линии параллельны соответствующим осям Сх и Су. Пусть эти линии пересекаются в некоторой точке D. Так как эта точка принадлежит двум нулевым линиям, то напряжения в ней от двух сил, одновременно приложенных в точках А и В, равны нулю. Приложим теперь силу F в точке К, лежащей на прямой АВ. Эту силу можно разложить на две составляющие, приложенные точках А и В. От этих двух составляющих, а следовательно, и от их равнодействующей напряжения в точке D будут равны нулю. Так как точка К была взята произвольно, то при любом положении силы F на прямой АВ напряжение в точке D равно нулю. Следовательно, при движении силы F по прямой АВ нулевая линия вращается вокруг точки D.
Полученные выводы о поведении нулевой линии, связанные с перемещением
по сечению сжимающей силы используются при анализе внецентренного сжатия.
10.3.3. Ядро сечения
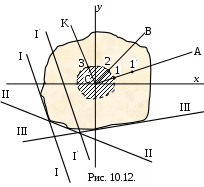
Рассмотрим случай внецентренного сжатия массивной колонны произвольного поперечного сечения. Предположим, что сила F перемещается из центра тяжести поперечного сечения по прямой CА (рис. 10.12.), в это время нулевая линия также будет перемещаться из бесконечности по направлению к центру тяжести сечения, оставаясь всё время параллельной первоначальному своему положению.
Наступит такой момент, когда нулевая линия в какой-либо точке коснётся сечения и займёт положение I-I. Этому положению нулевой линии на прямой CА соответствует точка, к которой приложена сила F. Если груз передвинуть за точку 1, ещё дальше от центра тяжести в точку 1, то нулевая линия дополнительно переместится (I- I), войдёт внутрь поперечного сечения и разделит сечение на две части: сжатую и растянутую. Точно так же на прямых CВ и СK можно определить граничные точки 2 и 3, которые обладают теми же свойствами, что и точка 1.
Если мысленно провести бесчисленное множество прямых, исходящих из точки C, и определить их граничные точки, то геометрическое место этих точек образую кривую, которая вокруг центра тяжести сечения очертит некоторую область, называемую ядром сечения. Всякая сжимающая сила, приложенная где-либо внутри ядра сечения, вызывает во всём сечении только сжимающие напряжения. От растягивающей силы, приложенной внутри ядра сечения, возникаю только растягивающие напряжения.
Таким образом, ядром сечения называется область, очерченная вокруг центра тяжести и характерная тем, что всякая продольная сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения напряжения одного знака.
В тех случаях, когда колонна изготавливается из материала, плохо работающего на растяжение (например, бетон ,камень, кирпич и т.п.), очень важно знать заранее размеры ядра сечения и его форму.
Рассмотрим часто встречающийся случай: прямоугольное сечение
(рис. 11.13,а) со сторонами bиh. Рассмотрим четыре положения касательной, совмещенной со сторонами прямоугольника.
Для касательной I-I отрезки, отсекаемые на осях координат, равны ах= ау= h/2. Координаты первой вершины ядра сечения определяются по формулам:
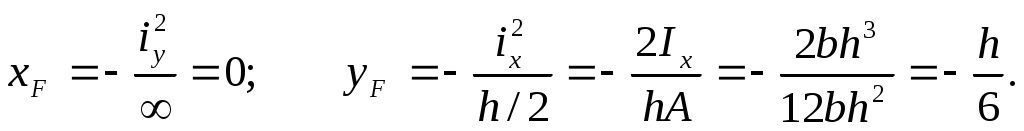
Таким образом, точка 1 лежит на оси су на расстоянии h/6 от оси сх, это расстояние откладывается в сторону, противоположную касательной I-I (рис. 10.13,а).
Точно так же точка 3 для касательной III-III будет лежать на оси у и также на расстоянии h/6 от оси сх.
Если повторить все рассуждения по отношению к касательной II-II и IV-IV и найти вершины ядра сечения, то получим xF= b/6
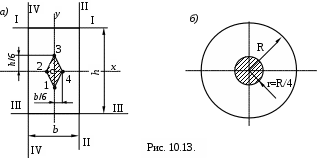
Построим ядро сечения для круглого сплошного сечения (рис. 10.13,б).
Ввиду того, что круг симметричен относительно центра (полярная симметрия), достаточно рассмотреть одно произвольное положение касательной (рис. 10.13,б)).
Расстояние до границы ядра сечения равно

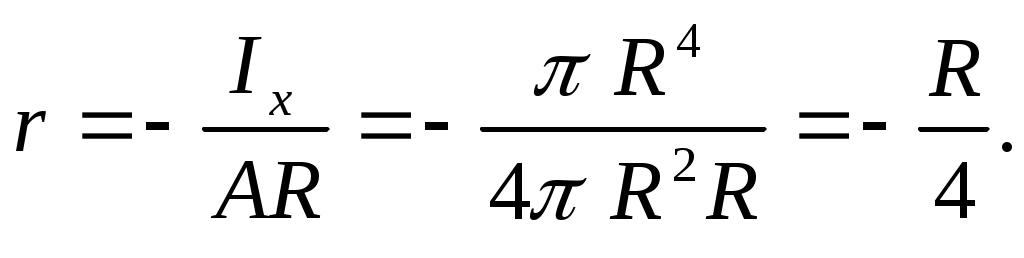
Таким образом, ядро сечения для круга радиуса R очерчено также по окружности радиусаr.
10.4. Одновременное действие кручения с изгибом
Одновременное действие кручения с изгибом чаще всего встречается в различных деталях машин.
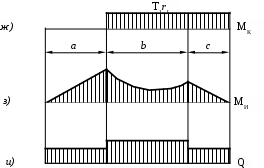
На рисунке 10.14. указаны действующие в отдельных его сечениях силовые факторы и построены эпюры изгибающих моментов, крутящего момента и поперечных сил.
Общая последовательность операций при построении эпюр такова. Сначала необходимо все внешние силы, приложенные к валу со шкивами
, привести к центрам тяжести соответствующих сечений. Затем находятся опорные реакции отдельно для сил, лежащих в плоскости YZ , и для сил, лежащих в плоскости XZ. В результате получается расчетная схема действия внешних сил на вал изображенная на рис. 10.14, б). Далее, для сил, лежащих в плоскости YZ , строятся эпюры Qy (рис. в)) и Мх(рис. 11.14, г)). Аналогичным образом для сил, лежащих в плоскости XZ, строятся эпюры Qх (рис. 10.14, д)) и Му (рис. 10.14, е)).
Для моментов, лежащих в плоскости XY, строится эпюр крутящих моментов Мк (рис. 10.14, ж)).
Учитывая, что для круглого вала любая ось, проходящая через центр его тяжести, является главной центральной, можно в каждом поперечном сечении геометрически сложить изгибающие моменты Мхи Му
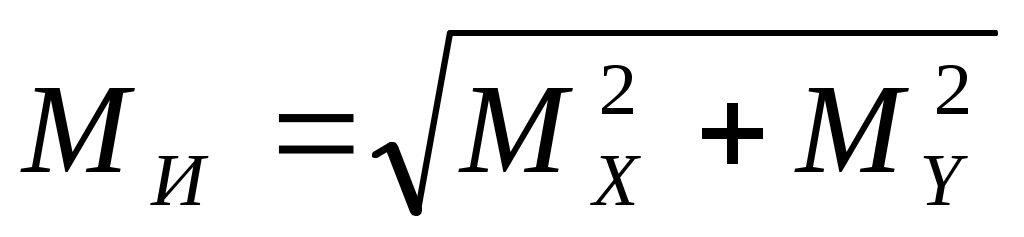
и поперечные силы Qx и Qу
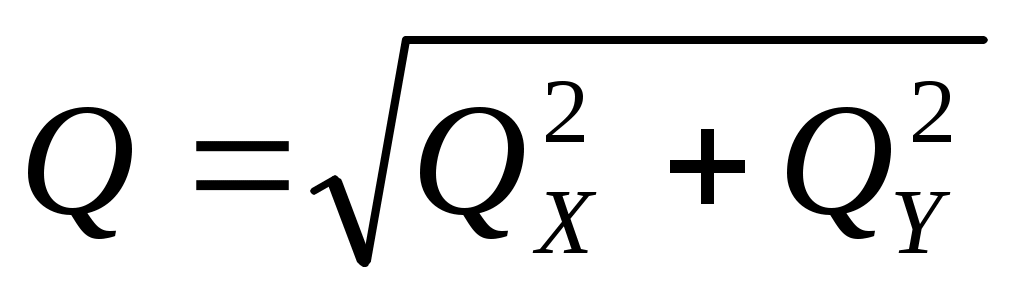 .
.
В результате применения этих формул могут быть построены эпюры
МИ (рис. 10.14, з)) и Q (рис. 10.14, и)). При их построении надо иметь в виду следующие обстоятельства.
Максимальные напряжения от изгибающего момента имеют место в двух диаметрально противоположных точках контура сечения и по величине равны:
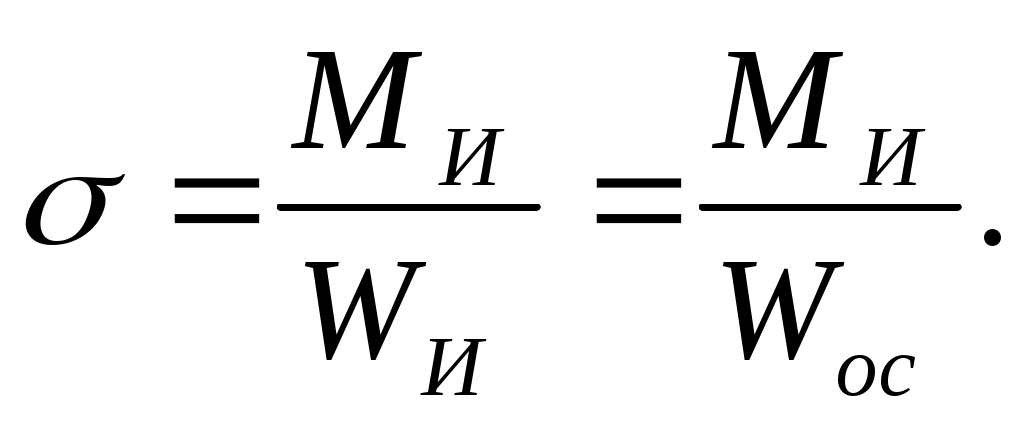 (10.12)
(10.12)
Крутящий момент МК вызывает наибольшие касательные напряжения во всех точках сечения:
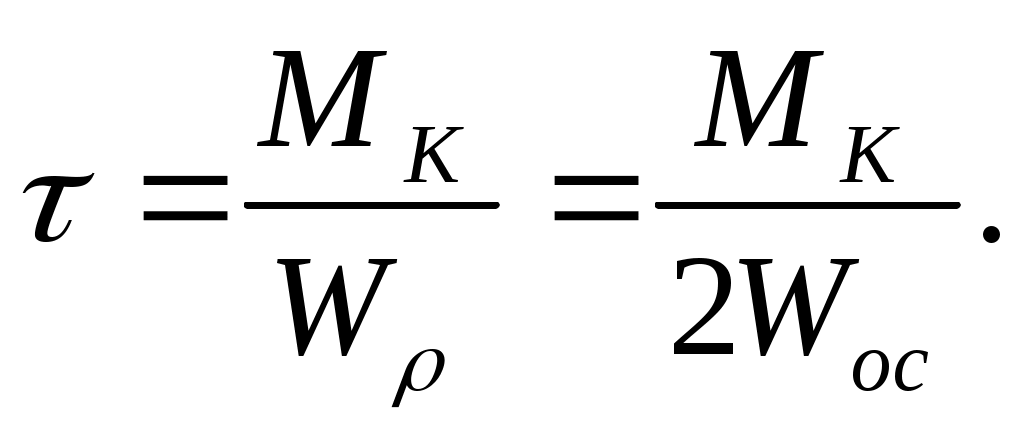
(10.13)
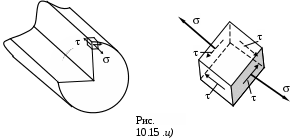
Сделаем некоторую небольшую ошибку в запас прочности, принимая, что точки с наибольшим нормальным и касательным напряжением совпадают, получим двухосное напряженное состояние (см.рис. 10.15), которое требует для проверки прочности одну из теорий прочности. Имея в виду,что валы изготовлены из стали, применяем третью или четвертую теорию прочности. Для этого необходимо определить главные напряжения.
Так как опасная точка сечения оказывается одна из точек контура (рис.10.15), то главные напряжения в опасной точке найдутся по уже известным формулам:
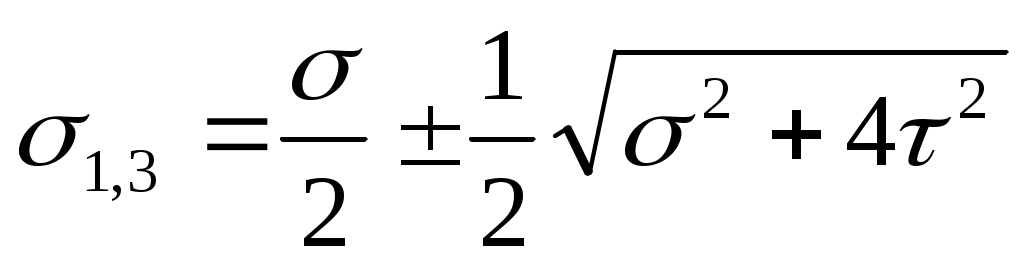 (10.14)
(10.14)
2=0
Условие прочности, по третьей гипотезе (гипотезе набольших касательных напряжений),
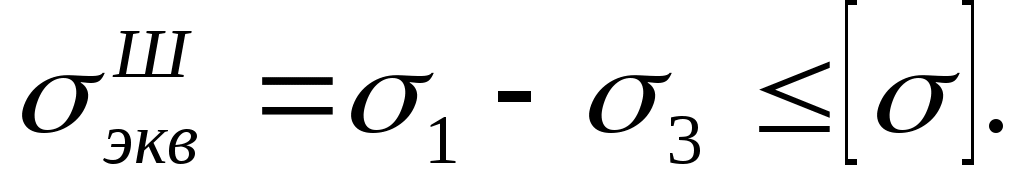
Подставляя сюда значения 1 и 3, получаем
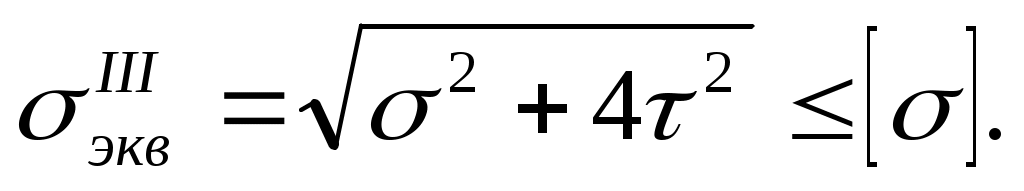 (10.15)
(10.15)
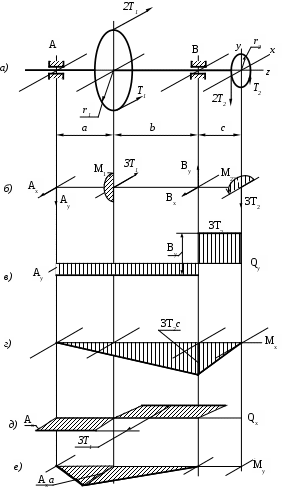
Рис. 10.14
П
Рис. 10.14
родолжение рисунка
Учитывая (1) и (2), получаем
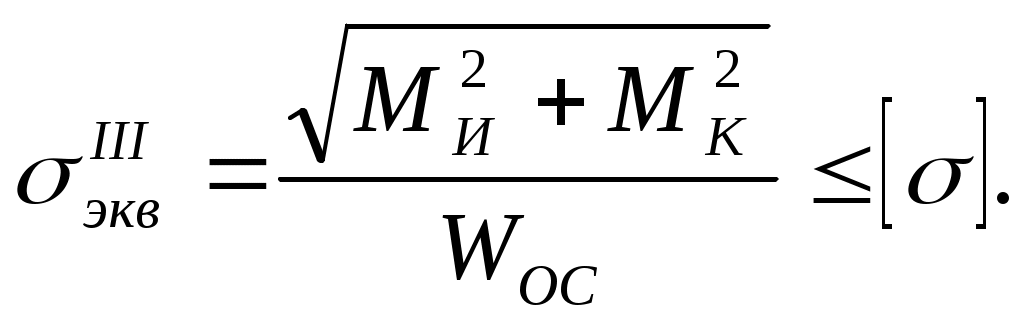
 (10.16)
(10.16)
Отсюда получим зависимость для подбора сечения (проектного расчета):
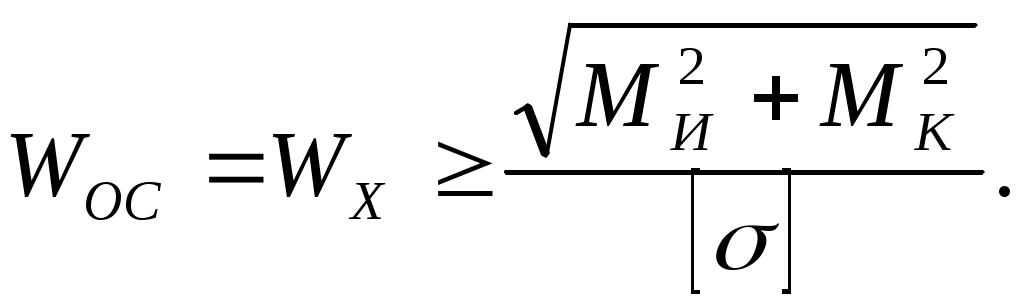 (10.17) По четвёртой гипотезе прочности (гипотезе удельной потенциальной энергии изменения формы), условие прочности для случая плоского напряженного состояния имеет вид
(10.17) По четвёртой гипотезе прочности (гипотезе удельной потенциальной энергии изменения формы), условие прочности для случая плоского напряженного состояния имеет вид
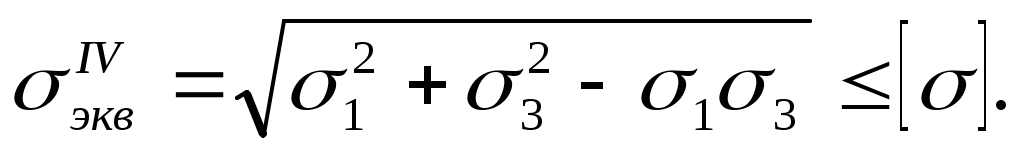 (10.18)
(10.18)
Подставляя сюда значения 1 и 3, получаем
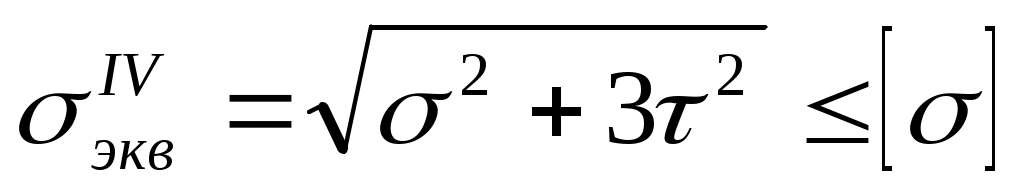 (10.19)
(10.19)
Учитывая (1) и (2), получаем
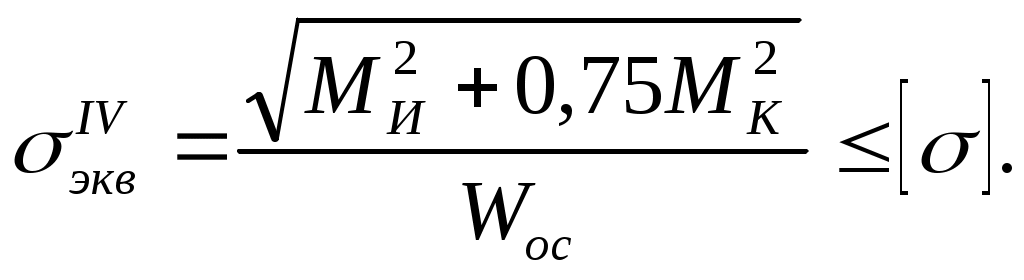 (10.20)
(10.20)
Отсюда для подбора сечения
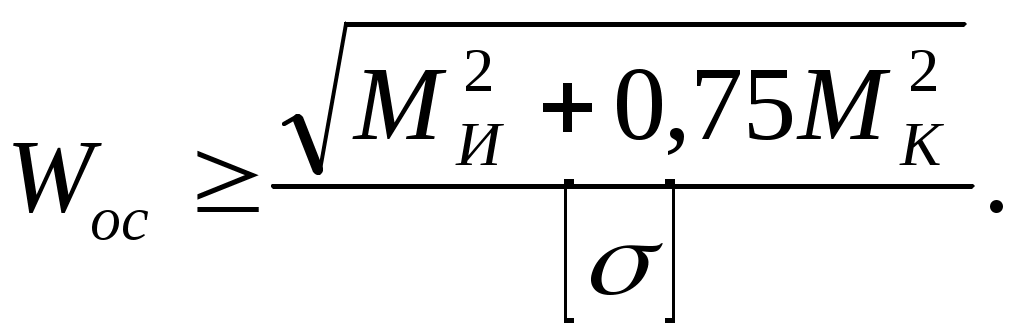 (10.21)
(10.21)
Для материалов, имеющих различную прочность на растяжение и сжатие (некоторые сорта легированной стали, чугун, некоторые сплавы), следует пользоваться гипотезой Мора.
По гипотезе Мора,
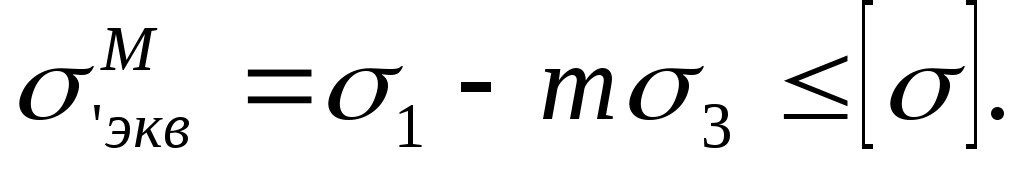 ,
,
где m=[P]/ [C] - отношение допускаемых напряжений.
10.5._Расчёт_цилиндрических_винтовых_пружин'>10.5. Расчёт цилиндрических винтовых пружин
10.5.1. Расчёт на прочность
Винтовая пружина представляет собой кривой брус, ось которого имеет форму винтовой линии. Предположим, что пружина работает под действием осевых сил F, приложенных к концам пружины.
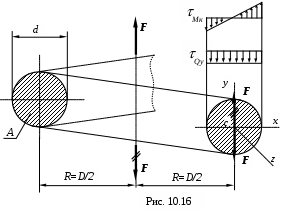
Рассечём мысленно пруток (виток) плоскостью (см. рис. 10.16), проходящей через ось пружины, и отбросим нижнюю часть пружины. Верхняя часть будет находится в равновесии под действием внешней силы F и внутренних сил, приведённых к центру тяжести сечения прутка. Для упрощения расчёта будем предполагать, что угол наклона витков близок к 900. Это позволяет рассматривать момент М=FR –как крутящий момент МК, а силу F –как поперечную силу QУ .
Сила Qy=F вызывает в сечении касательные напряжения Qy ; приближённо будем считать эти напряжения распределёнными равномерно по всему сечению прутка:
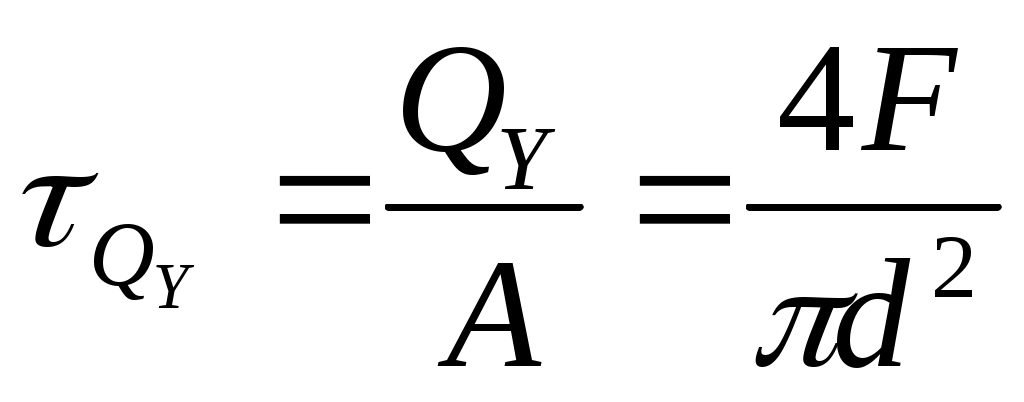 (10.22)
(10.22)
Кроме того, в сечении прутка возникают касательные напряжения Мк , связанные с наличием крутящего момента МК=FR=F(D/2), который вызван парой сил, зачёркнутыми дважды, и равные
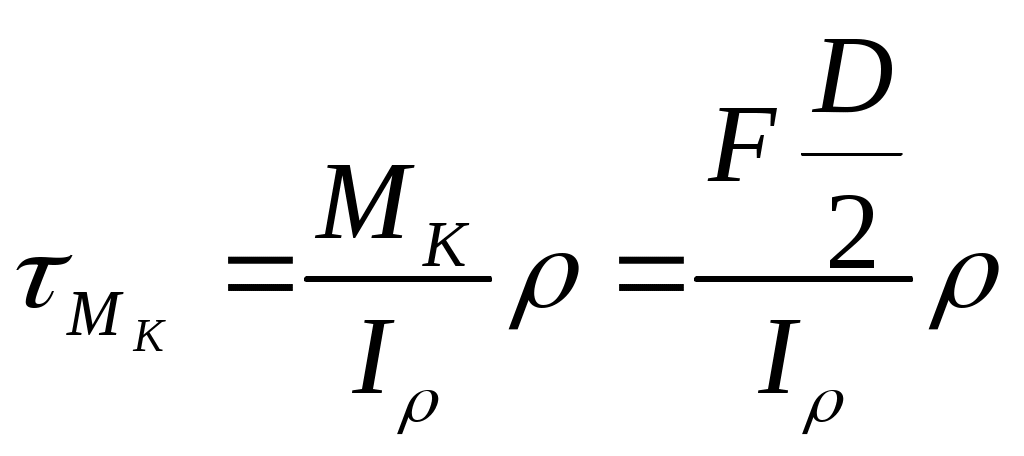 (10.23)
(10.23)
Наибольшие напряжения Мк возникают у боковой поверхности, где они равны
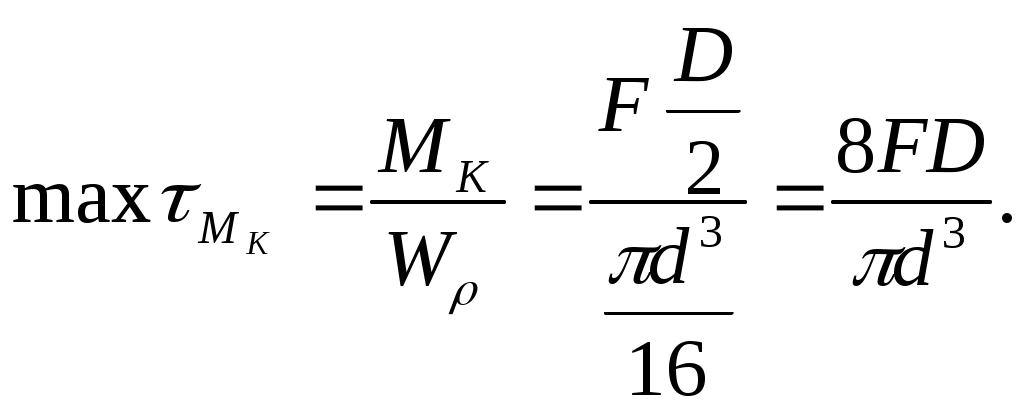
Таким образом, суммарное напряжение на внутренней поверхности имеет наибольшее значение и тогда уравнение прочности примет вид
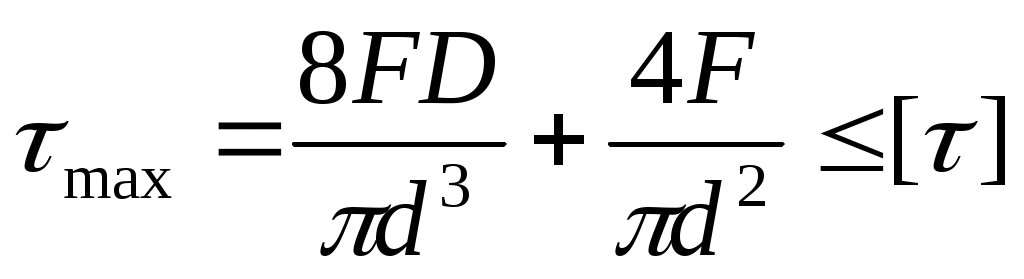 (10.24)
(10.24)
или
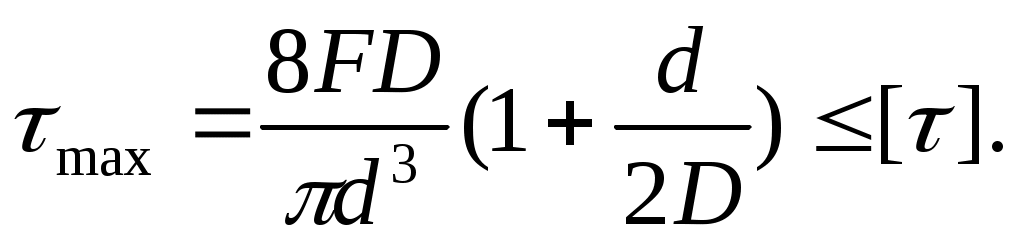 (10.25)
(10.25)
Так как обычно отношение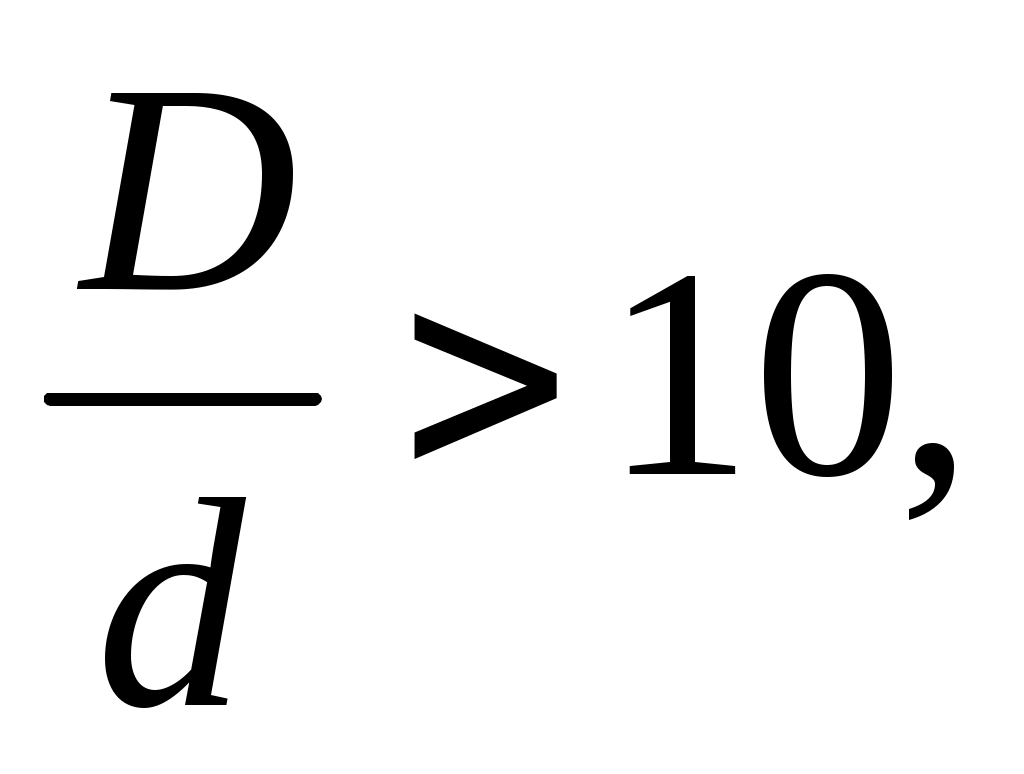 то второе слагаемое в скобках значительно меньше единицы, поэтому им можно пренебречь. Тогда расчетная формула на прочность пружины
то второе слагаемое в скобках значительно меньше единицы, поэтому им можно пренебречь. Тогда расчетная формула на прочность пружины
Полученные выводы о поведении нулевой линии, связанные с перемещением
по сечению сжимающей силы используются при анализе внецентренного сжатия.
10.3.3. Ядро сечения

Рассмотрим случай внецентренного сжатия массивной колонны произвольного поперечного сечения. Предположим, что сила F перемещается из центра тяжести поперечного сечения по прямой CА (рис. 10.12.), в это время нулевая линия также будет перемещаться из бесконечности по направлению к центру тяжести сечения, оставаясь всё время параллельной первоначальному своему положению.
Наступит такой момент, когда нулевая линия в какой-либо точке коснётся сечения и займёт положение I-I. Этому положению нулевой линии на прямой CА соответствует точка, к которой приложена сила F. Если груз передвинуть за точку 1, ещё дальше от центра тяжести в точку 1, то нулевая линия дополнительно переместится (I- I), войдёт внутрь поперечного сечения и разделит сечение на две части: сжатую и растянутую. Точно так же на прямых CВ и СK можно определить граничные точки 2 и 3, которые обладают теми же свойствами, что и точка 1.
Если мысленно провести бесчисленное множество прямых, исходящих из точки C, и определить их граничные точки, то геометрическое место этих точек образую кривую, которая вокруг центра тяжести сечения очертит некоторую область, называемую ядром сечения. Всякая сжимающая сила, приложенная где-либо внутри ядра сечения, вызывает во всём сечении только сжимающие напряжения. От растягивающей силы, приложенной внутри ядра сечения, возникаю только растягивающие напряжения.
Таким образом, ядром сечения называется область, очерченная вокруг центра тяжести и характерная тем, что всякая продольная сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения напряжения одного знака.
В тех случаях, когда колонна изготавливается из материала, плохо работающего на растяжение (например, бетон ,камень, кирпич и т.п.), очень важно знать заранее размеры ядра сечения и его форму.
Рассмотрим часто встречающийся случай: прямоугольное сечение
(рис. 11.13,а) со сторонами bиh. Рассмотрим четыре положения касательной, совмещенной со сторонами прямоугольника.
Для касательной I-I отрезки, отсекаемые на осях координат, равны ах= ау= h/2. Координаты первой вершины ядра сечения определяются по формулам:
Таким образом, точка 1 лежит на оси су на расстоянии h/6 от оси сх, это расстояние откладывается в сторону, противоположную касательной I-I (рис. 10.13,а).
Точно так же точка 3 для касательной III-III будет лежать на оси у и также на расстоянии h/6 от оси сх.
Если повторить все рассуждения по отношению к касательной II-II и IV-IV и найти вершины ядра сечения, то получим xF= b/6

Построим ядро сечения для круглого сплошного сечения (рис. 10.13,б).
Ввиду того, что круг симметричен относительно центра (полярная симметрия), достаточно рассмотреть одно произвольное положение касательной (рис. 10.13,б)).
Расстояние до границы ядра сечения равно
Таким образом, ядро сечения для круга радиуса R очерчено также по окружности радиусаr.
10.4. Одновременное действие кручения с изгибом
Одновременное действие кручения с изгибом чаще всего встречается в различных деталях машин.
На рисунке 10.14. указаны действующие в отдельных его сечениях силовые факторы и построены эпюры изгибающих моментов, крутящего момента и поперечных сил.
Общая последовательность операций при построении эпюр такова. Сначала необходимо все внешние силы, приложенные к валу со шкивами
, привести к центрам тяжести соответствующих сечений. Затем находятся опорные реакции отдельно для сил, лежащих в плоскости YZ , и для сил, лежащих в плоскости XZ. В результате получается расчетная схема действия внешних сил на вал изображенная на рис. 10.14, б). Далее, для сил, лежащих в плоскости YZ , строятся эпюры Qy (рис. в)) и Мх(рис. 11.14, г)). Аналогичным образом для сил, лежащих в плоскости XZ, строятся эпюры Qх (рис. 10.14, д)) и Му (рис. 10.14, е)).
Для моментов, лежащих в плоскости XY, строится эпюр крутящих моментов Мк (рис. 10.14, ж)).
Учитывая, что для круглого вала любая ось, проходящая через центр его тяжести, является главной центральной, можно в каждом поперечном сечении геометрически сложить изгибающие моменты Мхи Му
и поперечные силы Qx и Qу
В результате применения этих формул могут быть построены эпюры
МИ (рис. 10.14, з)) и Q (рис. 10.14, и)). При их построении надо иметь в виду следующие обстоятельства.
-
Суммарная поперечная сила Q может не лежать в плоскости действия суммарного изгибающего момента МИ, и поэтому между ними не будет соблюдаться зависимость ( dM/dz)=Q. -
Эпюра суммарного изгибающего момента МИ будет изображаться прямой линией на тех участках, на которых эпюры Мх и Му также изображены прямыми линиями с общей нулевой точкой (например 1-й участок). -
На тех участках, где эпюры Мх и Му изображаются прямыми линиями, но имеют нулевые точки в разных сечениях и плоскостях (например, 2-й участок), эпюра МИ будет изображаться вогнутой кривой, т. е. будет иметь набольшую ординату на одном из концов участка, и строится по точкам. -
Эпюры МИ иQ строятся по абсолютным значениям этих величин, т. е. они всегда положительны.
Максимальные напряжения от изгибающего момента имеют место в двух диаметрально противоположных точках контура сечения и по величине равны:
Крутящий момент МК вызывает наибольшие касательные напряжения во всех точках сечения:
(10.13)
Сделаем некоторую небольшую ошибку в запас прочности, принимая, что точки с наибольшим нормальным и касательным напряжением совпадают, получим двухосное напряженное состояние (см.рис. 10.15), которое требует для проверки прочности одну из теорий прочности. Имея в виду,что валы изготовлены из стали, применяем третью или четвертую теорию прочности. Для этого необходимо определить главные напряжения.
Так как опасная точка сечения оказывается одна из точек контура (рис.10.15), то главные напряжения в опасной точке найдутся по уже известным формулам:
2=0
Условие прочности, по третьей гипотезе (гипотезе набольших касательных напряжений),
Подставляя сюда значения 1 и 3, получаем

Рис. 10.14
П
Рис. 10.14
родолжение рисунка


Учитывая (1) и (2), получаем
Отсюда получим зависимость для подбора сечения (проектного расчета):
Подставляя сюда значения 1 и 3, получаем
Учитывая (1) и (2), получаем
Отсюда для подбора сечения
Для материалов, имеющих различную прочность на растяжение и сжатие (некоторые сорта легированной стали, чугун, некоторые сплавы), следует пользоваться гипотезой Мора.
По гипотезе Мора,
где m=[P]/ [C] - отношение допускаемых напряжений.
10.5._Расчёт_цилиндрических_винтовых_пружин'>10.5. Расчёт цилиндрических винтовых пружин
10.5.1. Расчёт на прочность
Винтовая пружина представляет собой кривой брус, ось которого имеет форму винтовой линии. Предположим, что пружина работает под действием осевых сил F, приложенных к концам пружины.

Рассечём мысленно пруток (виток) плоскостью (см. рис. 10.16), проходящей через ось пружины, и отбросим нижнюю часть пружины. Верхняя часть будет находится в равновесии под действием внешней силы F и внутренних сил, приведённых к центру тяжести сечения прутка. Для упрощения расчёта будем предполагать, что угол наклона витков близок к 900. Это позволяет рассматривать момент М=FR –как крутящий момент МК, а силу F –как поперечную силу QУ .
Сила Qy=F вызывает в сечении касательные напряжения Qy ; приближённо будем считать эти напряжения распределёнными равномерно по всему сечению прутка:
Кроме того, в сечении прутка возникают касательные напряжения Мк , связанные с наличием крутящего момента МК=FR=F(D/2), который вызван парой сил, зачёркнутыми дважды, и равные
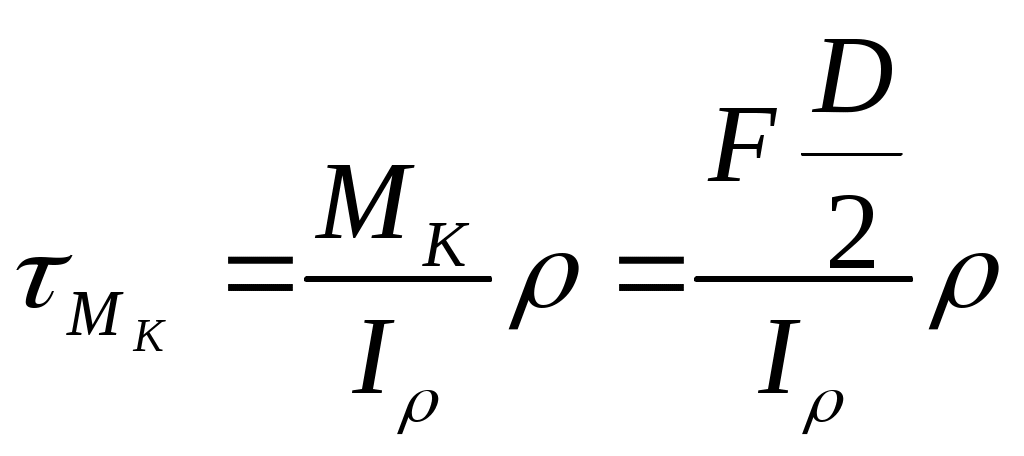 (10.23)
(10.23)Наибольшие напряжения Мк возникают у боковой поверхности, где они равны
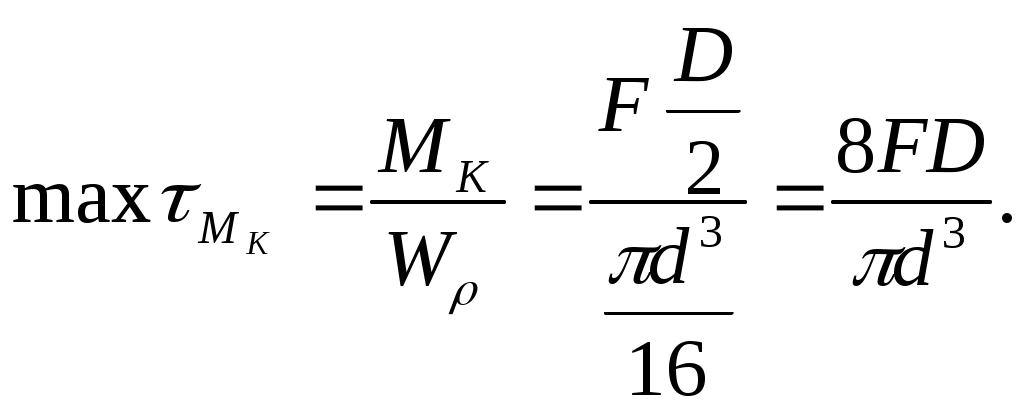
Таким образом, суммарное напряжение на внутренней поверхности имеет наибольшее значение и тогда уравнение прочности примет вид
или
Так как обычно отношение