Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 397
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
(13.8)
Условия r на внутренней и наружной поверхностях цилиндра (Г.У.).
Г.У. r=r1, r =-p1;
r=r2, r =-p2. (13.9)
Для определения постоянных А и В согласно (13.9) получим следующие два уравнения:
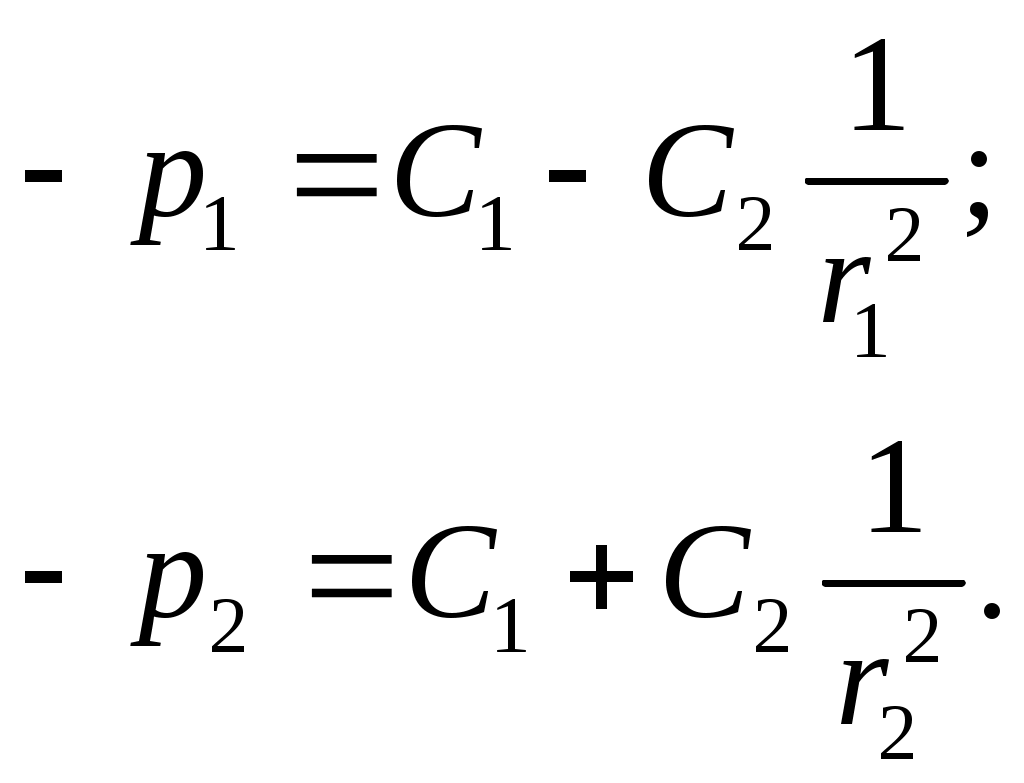
Решая эти уравнения относительно С1 и С2 , найдём :
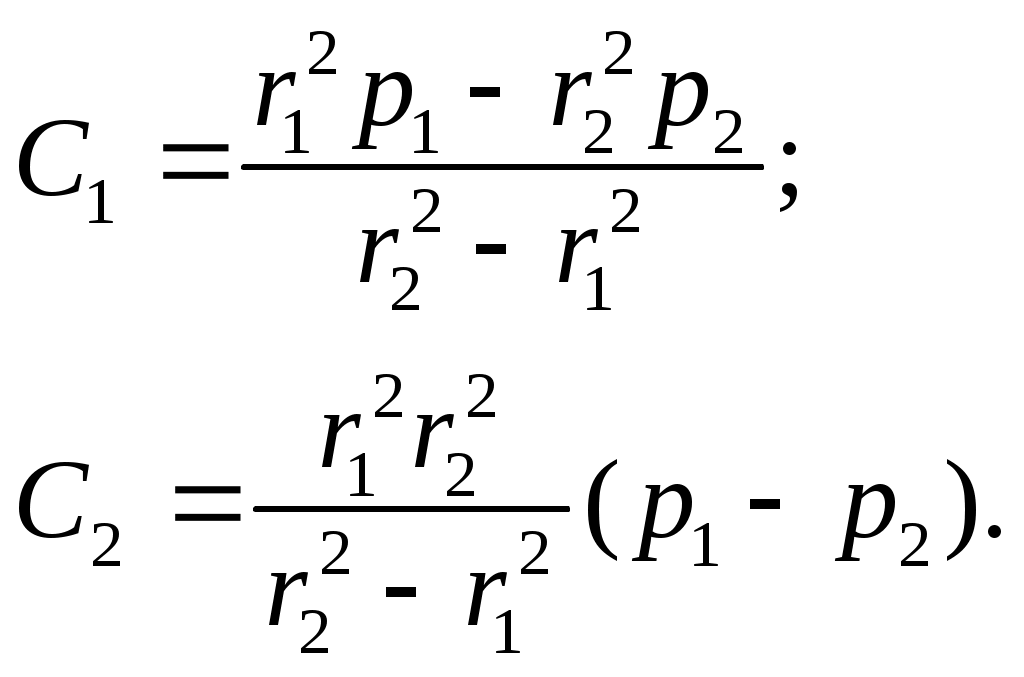
Подставляя значения постоянных в выражение (13.8), получим формулу для определения напряжений (формула Ляме)
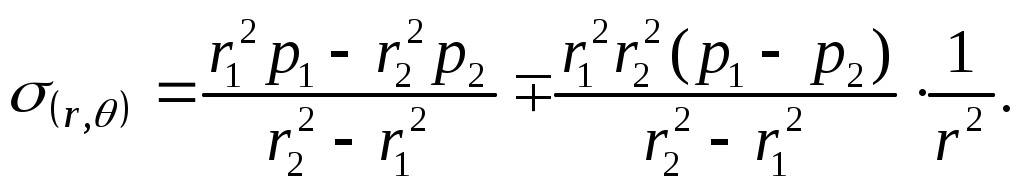 (13.10)
(13.10)
Аналогично, через решение (13.6), представив напряжения по формуле (13.4) и используя Г.У. (13.9), получим формулу (формула Ляме) для определения радиального перемещения
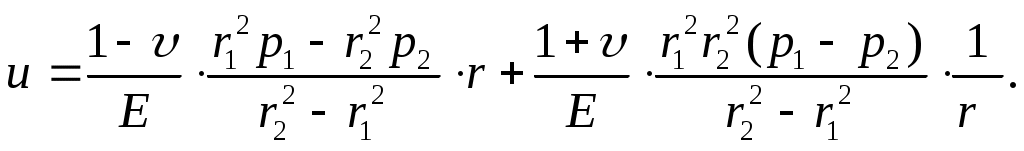 (13.11)
(13.11)
Сложив rи (см.формулу (13.10)) , убеждаемся, что их сумма величина постоянная, т.е.
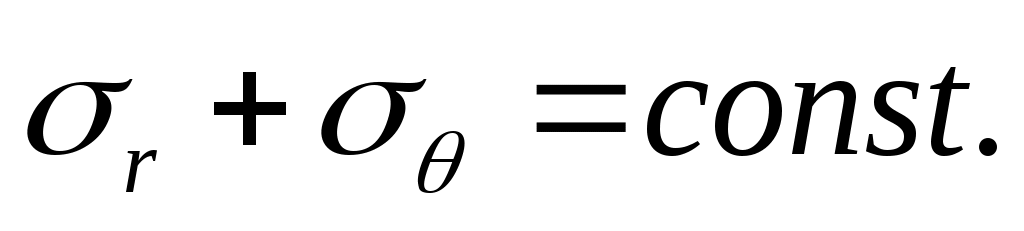 (13.12)
(13.12)
Относительная деформация рассматриваемого нами кольца в направлении, параллельном оси цилиндра, также будет постоянной на любом радиусе, т.е.
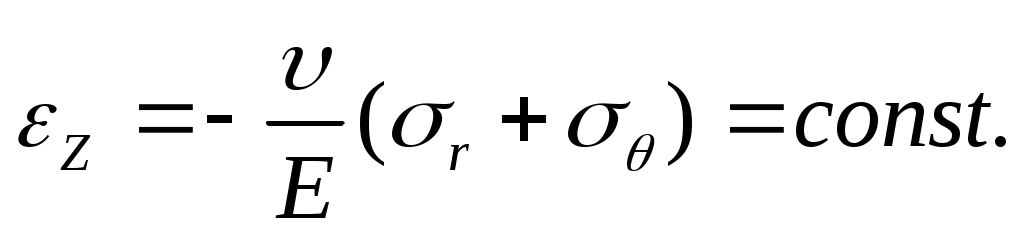 (13.13)
(13.13)
Н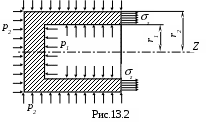 а основании этого цилиндр можно рассматривать как набранный из отдельных колец, нанизанных на ось. Поперечные сечения цилиндра при деформации остаются плоскими.
а основании этого цилиндр можно рассматривать как набранный из отдельных колец, нанизанных на ось. Поперечные сечения цилиндра при деформации остаются плоскими.
При наличии днища, т.е. закрытой трубы, в поперечных сечениях возникают осевые напряжения Z(рис. 13.2). Допуская их равномерное распределение по толщине стенки (что допустимо вдали от днищ) и составляя уравнение равновесия всех сил на ось Z, получаем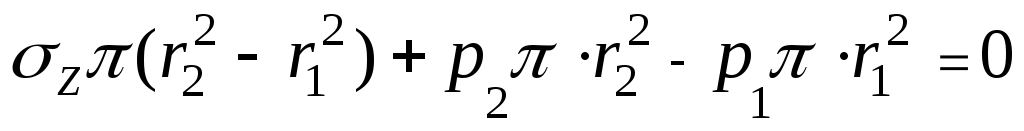
или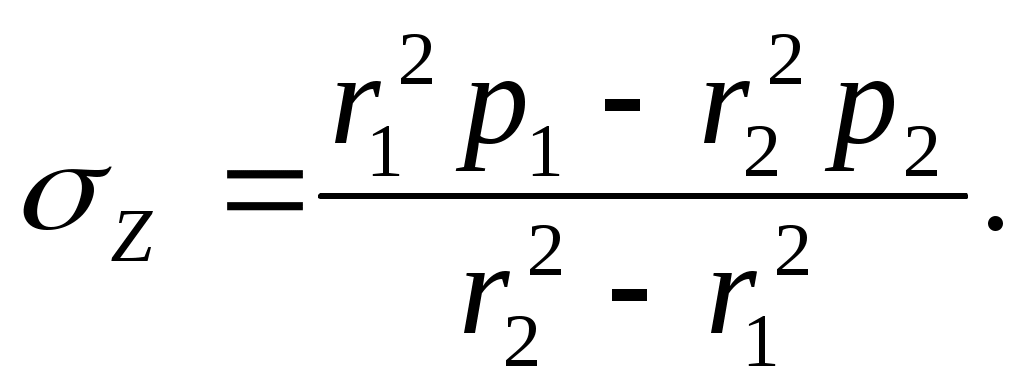
Сопоставление этой формулы с формулой Ляме (13.10) показывает, что главное осевое напряжение является средним арифметическим между окружным и радиальным
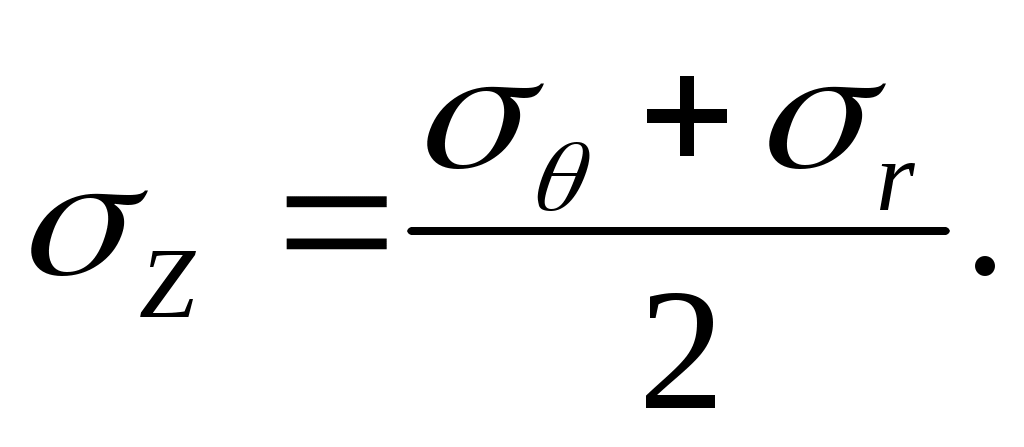
(13.14)
13.2. Определение напряжений и перемещений в толстостенном цилиндре
Рассмотрим два частных случая нагружения цилиндра (трубы).
1. Цилиндр (труба) нагружен только внутренним давлением.
В этом случае полагаем p1 = pи p2 = 0. Выражение (10) примет вид
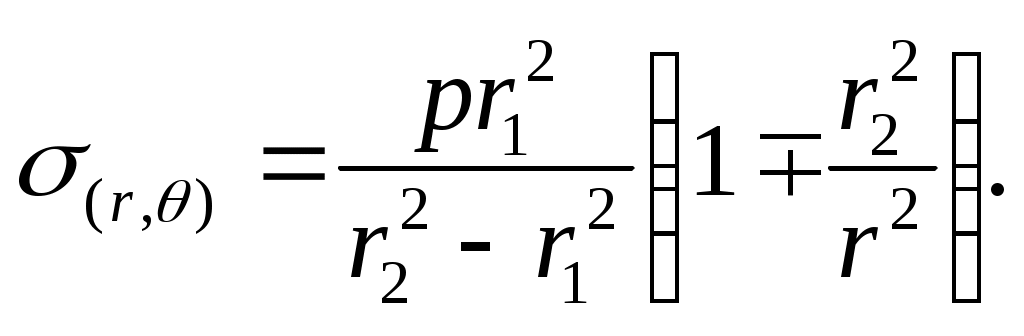
 (13.15)
(13.15)
Н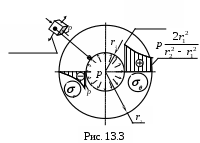
а рис. 13.3 показаны эпюры изменения радиального и окружного напряжения по толщине цилиндра при нагружении внутренним давлением.
Наиболее нагруженным оказывается внутренний слой, для которого

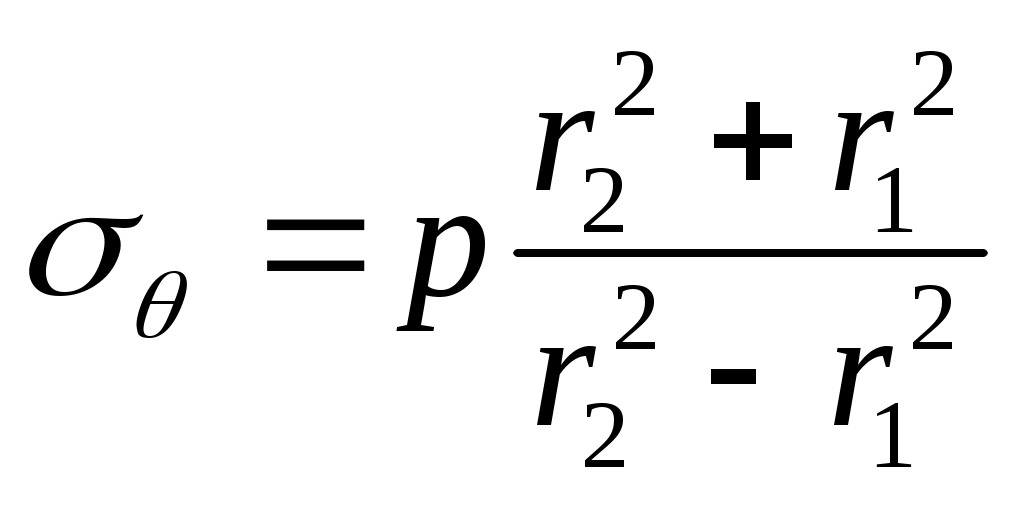 при r=r1,
при r=r1,
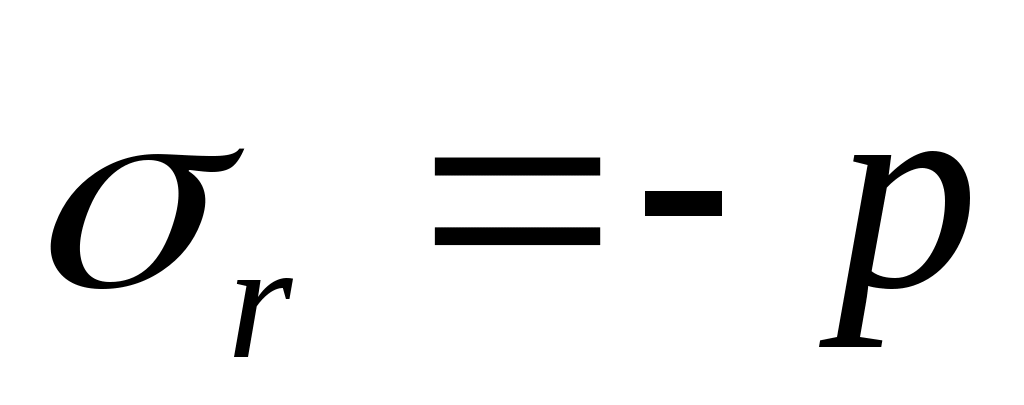 при r=r1.
при r=r1.
В этом случае получаем по теории наибольших касательных напряжений
(в случае отсутствия осевой силы т.е. при Z=0)
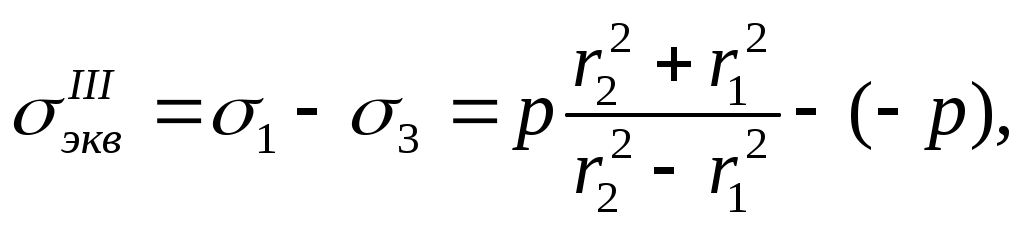
или
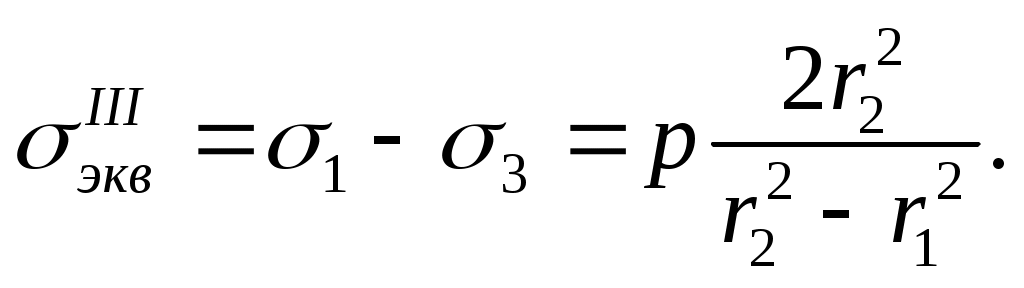 (13.16)
(13.16)
Радиальное перемещение у внутренней поверхности (увеличение внутреннего радиуса)
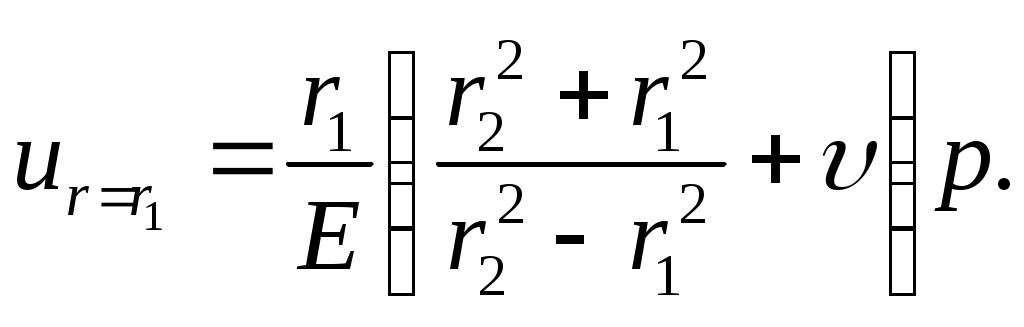 (13.17)
(13.17)
Напряжения и перемещения у наружной поверхности цилиндра следующие:
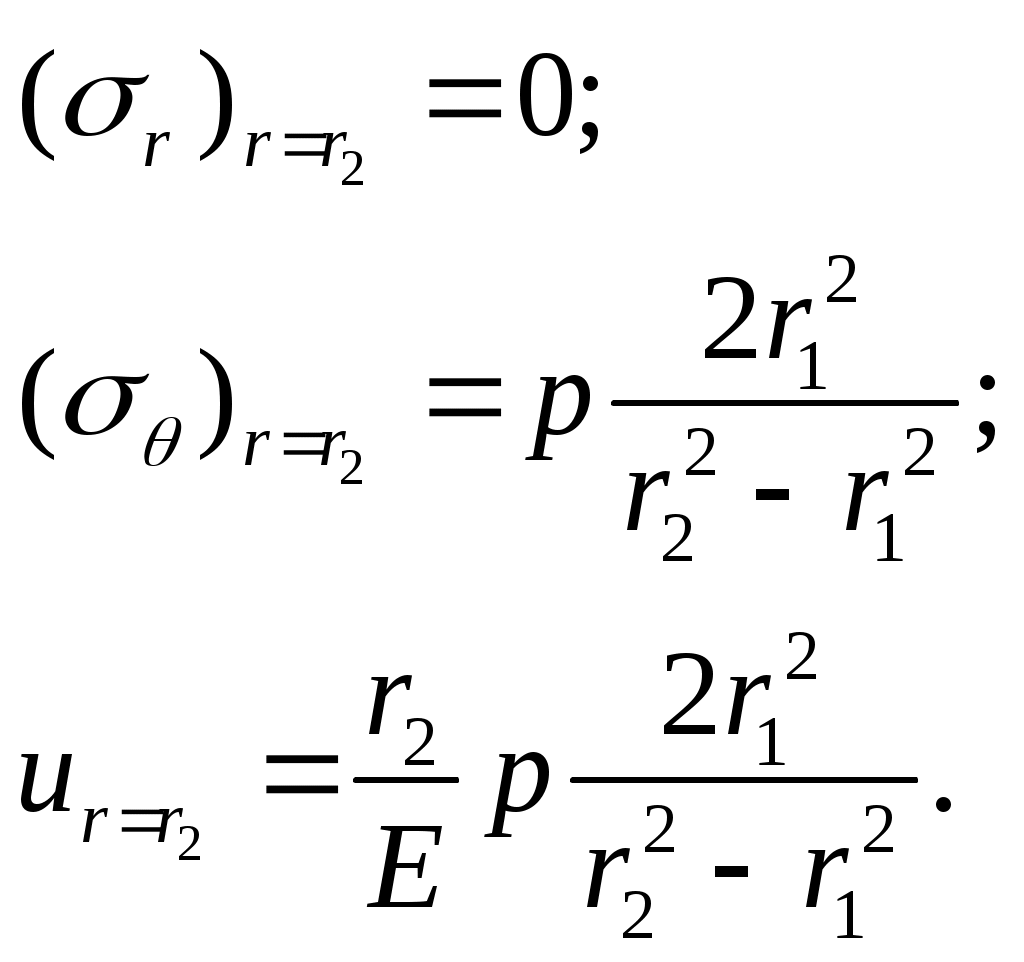 (13.18)
(13.18)
Напряжения при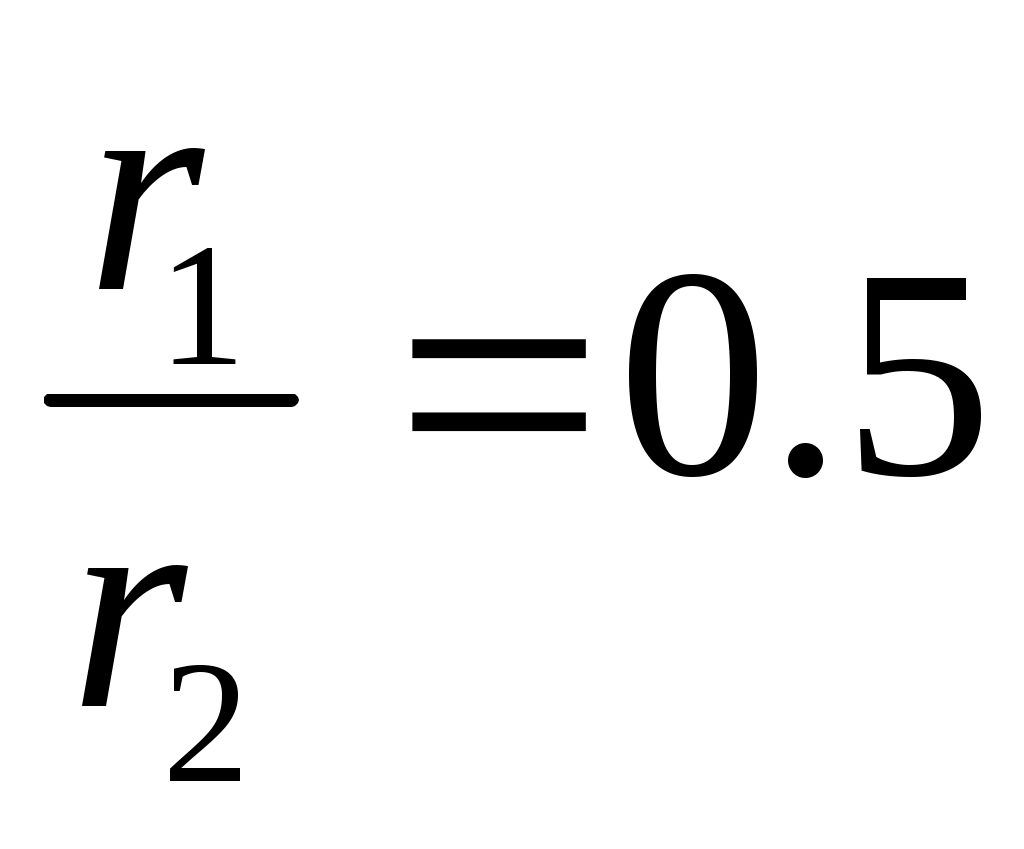 :
:
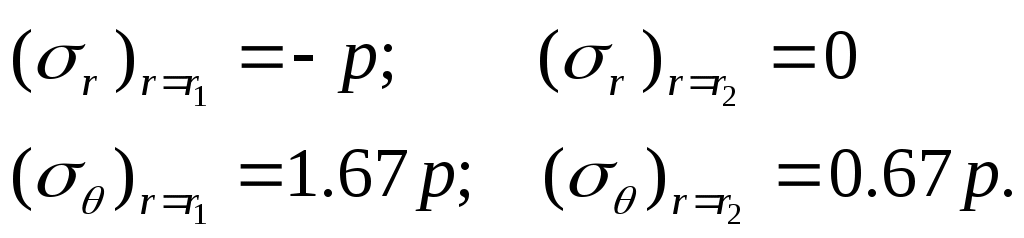
Если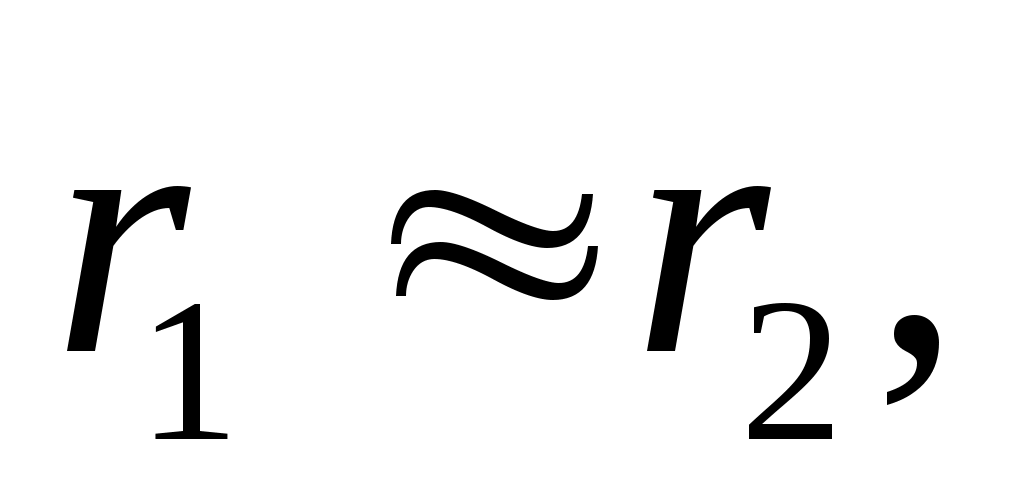 то
то 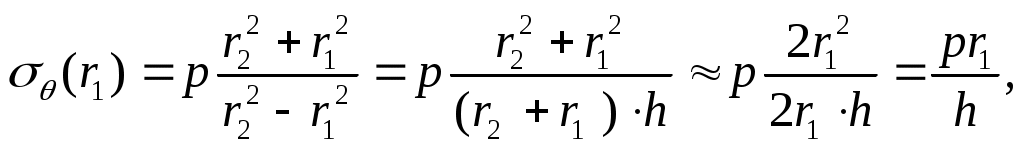
т.е.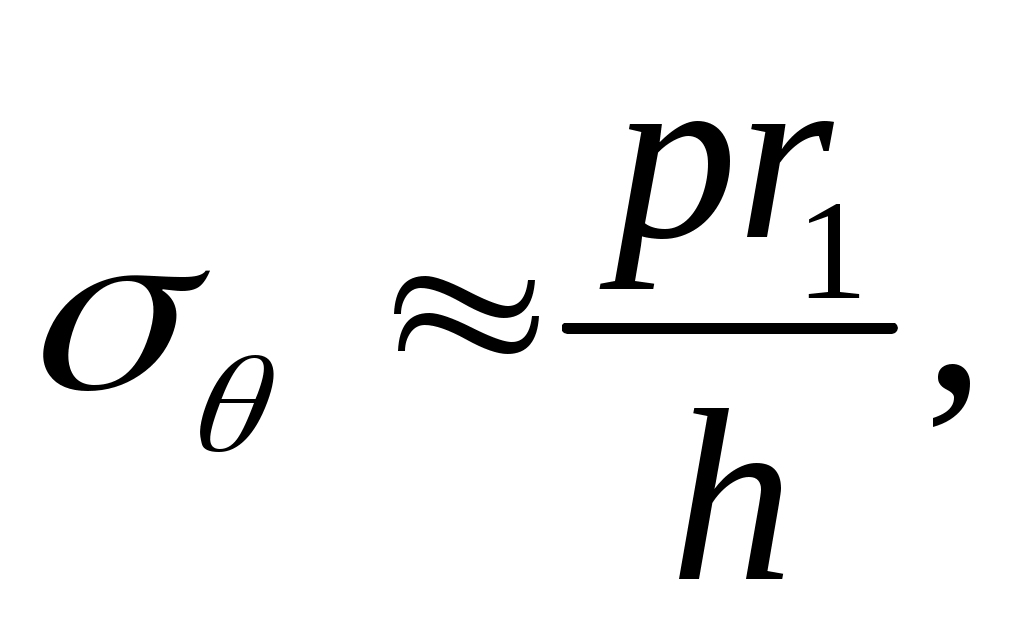 что соответствует формуле Лапласа для тонкостенных труб.
что соответствует формуле Лапласа для тонкостенных труб.
Рассмотрим случай, когда,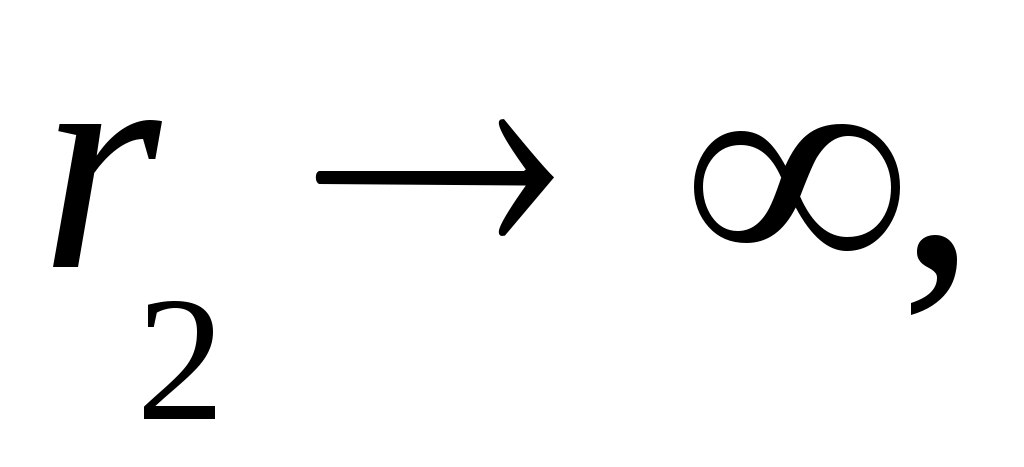
т.е. когда цилиндр имеет бесконечно большую толщину. Тогда выражение (13.15) принимает вид
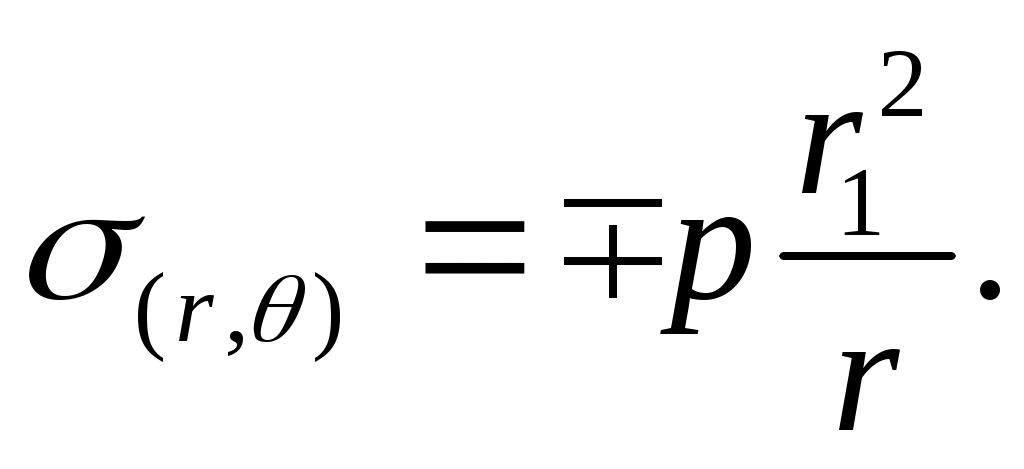
Это значит, что у цилиндра с бесконечно большой толщиной стенки при отсутствии осевых напряжений все точки находятся в состоянии чистого сдвига. Практически цилиндры с соотношением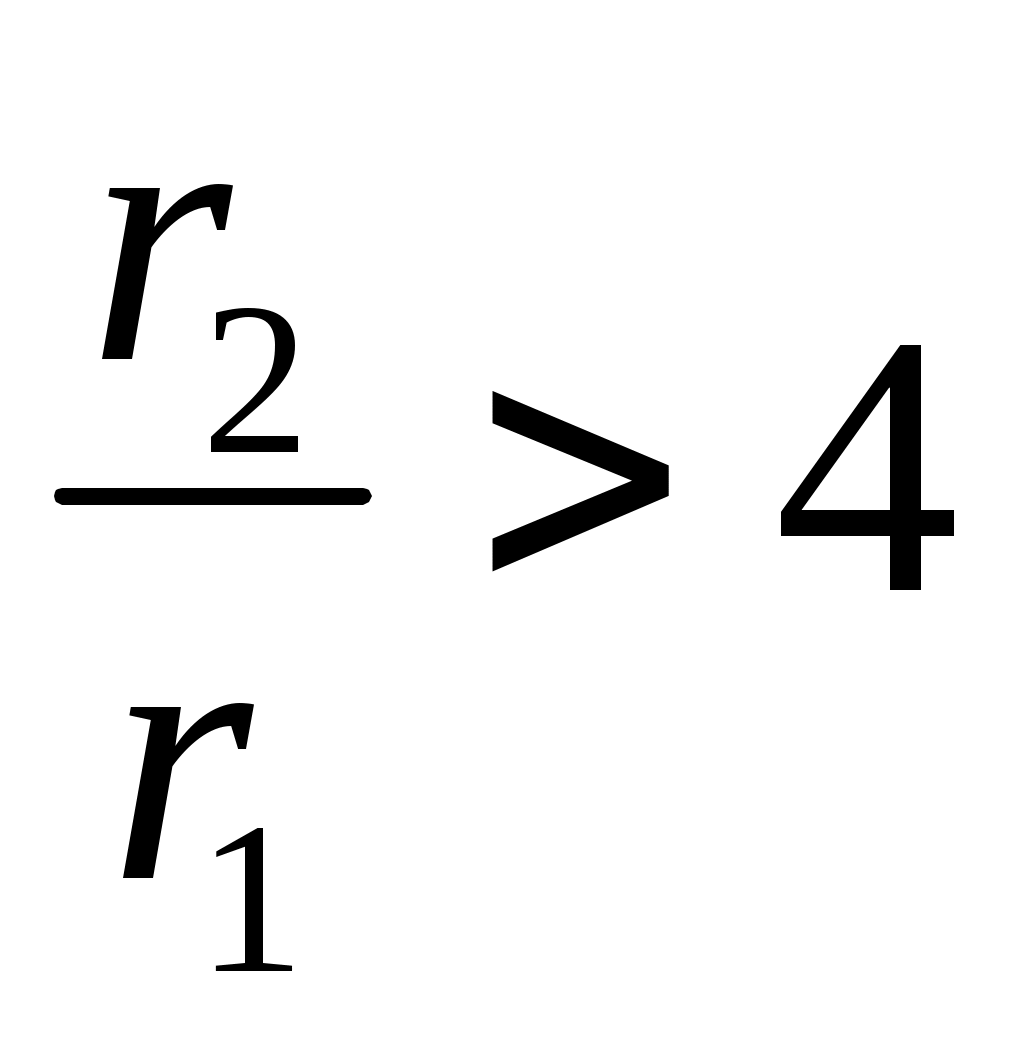 имеют разницу в напряжениях не более 5% и их можно уже рассматривать как цилиндры, имеющие бесконечно большую толщину стенки.
имеют разницу в напряжениях не более 5% и их можно уже рассматривать как цилиндры, имеющие бесконечно большую толщину стенки.
Эквивалентное напряжение согласно (13.16) при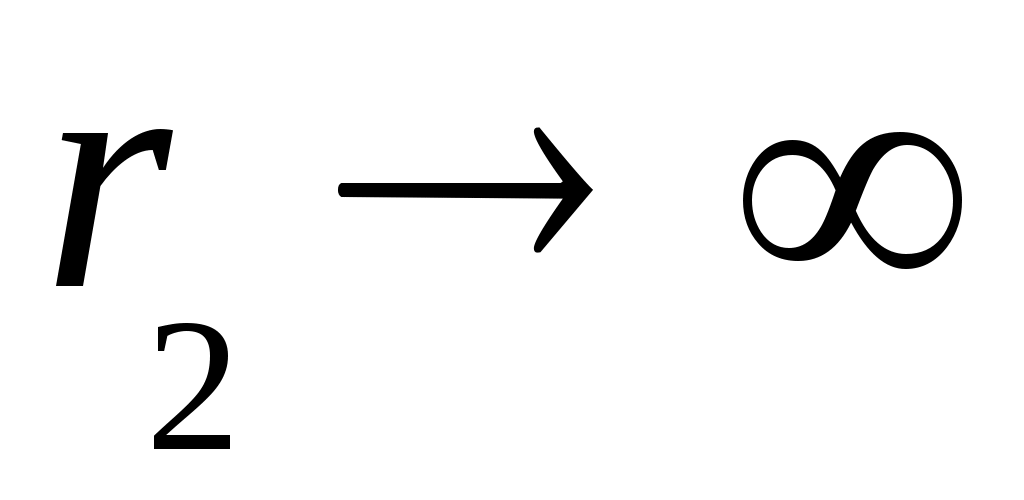 будет равно
будет равно
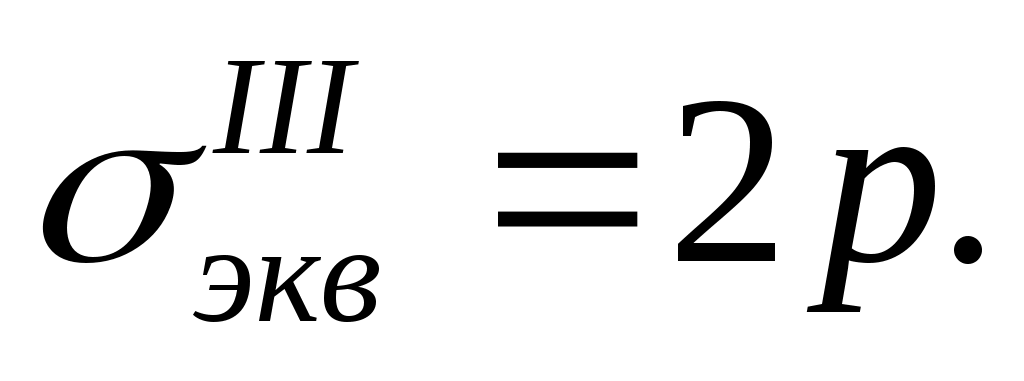
Е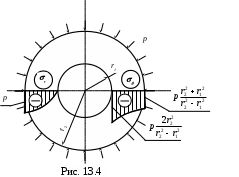 сли r2,
сли r2, 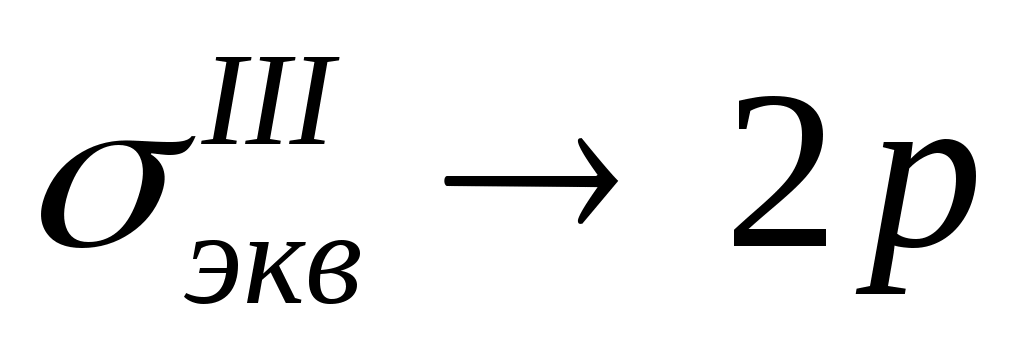 , т.е. привычный способ, путем изменения размеров, не позволяет уменьшить напряжения. Например, предел упругости
, т.е. привычный способ, путем изменения размеров, не позволяет уменьшить напряжения. Например, предел упругости  =600 МПа, то при бесконечно большой толщиной стенки цилиндра деформации будут упругими при давлении, не превышающем 300 МПа (3000 атм.).
=600 МПа, то при бесконечно большой толщиной стенки цилиндра деформации будут упругими при давлении, не превышающем 300 МПа (3000 атм.).
2. Цилиндр (труба) нагружен внешним давлением.
В этом случае полагаем p1 =0и p2 = p . Выражение (13.10) примет вид
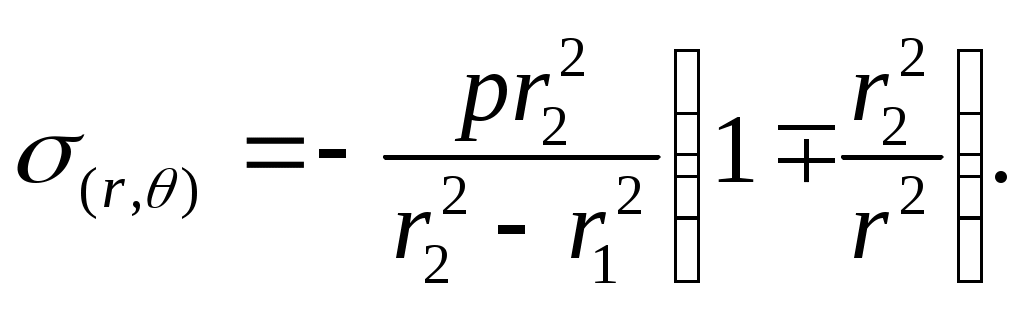 (13.19)
(13.19)
Эпюры напряжений по толщине цилиндра для этого случая нагружения представлены
на рис. 13.4.
Напряжения при :
:
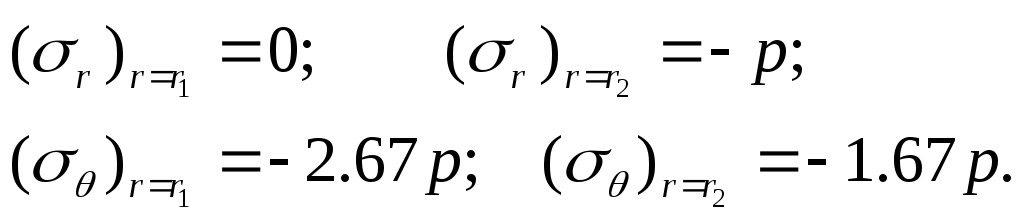
Наибольшее эквивалентное напряжение имеет место у внутренней поверхности цилиндра. При отсутствии осевой силы
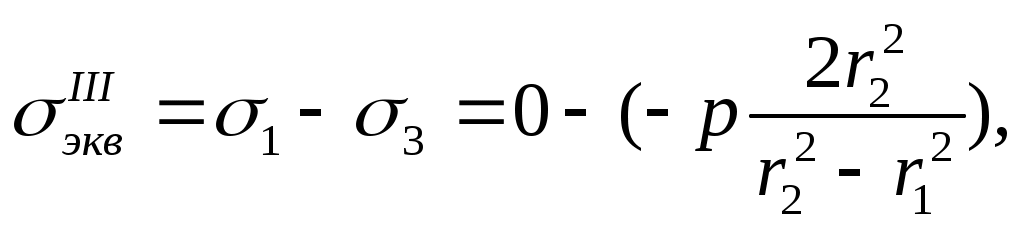
или

Это выражение совпадает с тем, которое было получено для случая внутреннего давления (смотри (13.16)) при r2,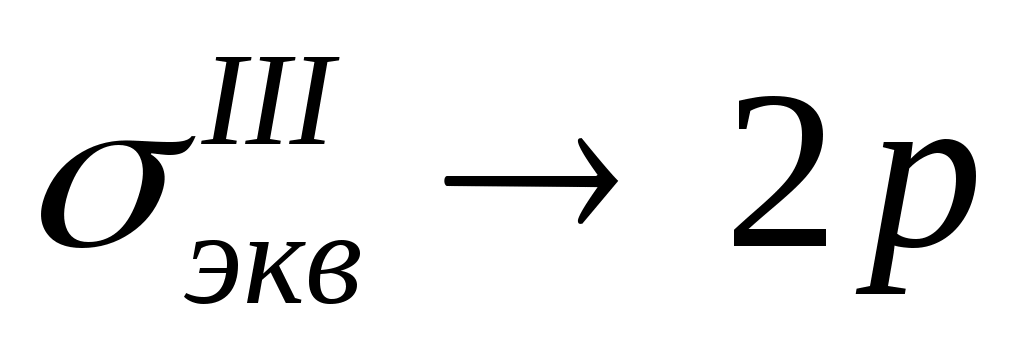 , т.е. привычный способ, путем изменения размеров, не позволяет уменьшить напряжения.
, т.е. привычный способ, путем изменения размеров, не позволяет уменьшить напряжения.
Формула для перемещений примет следующий вид:
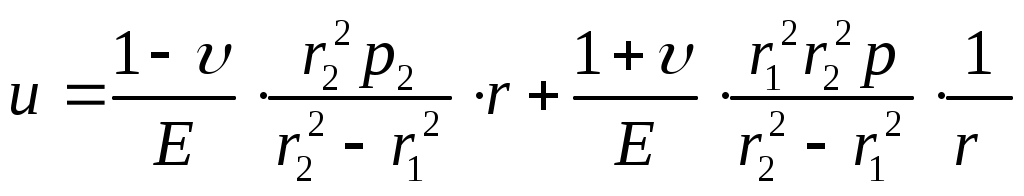 (13.20)
(13.20)
Если r1 0 (r1 =0), тогдаr= =-р (т.е. имеем гидростатическое напряженное состояние).
Формула для перемещений примет вид:
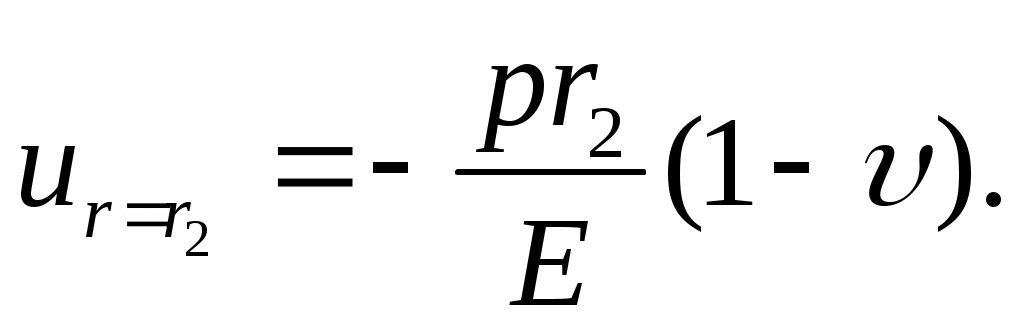 (13.21)
(13.21)
13.3. Определение напряжений в составных трубах
Выше мы показали, что увеличение толщины не может во всех случаях обеспечить необходимой прочности трубы. В пределe при бесконечно большой толщине ( )
) 
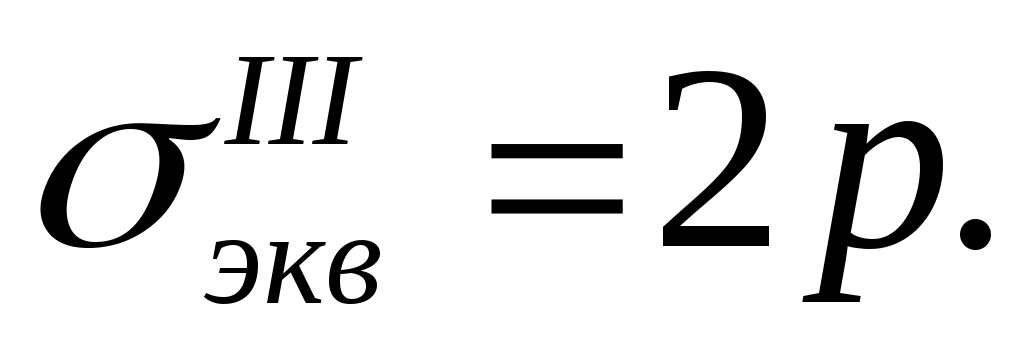 Привычный способ уменьшения напряжений увеличением размеров в данном случае не достигает цели. Следовательно, для сосудов высокого давления необходимо искать какие-то новые конструктивные решения. В середине позапрошлого столетия академиком А.К. Гадолиным была создана теория расчета артиллерийских стволов, составляемых из нескольких сопрягаемых толстостенных цилиндров, чем обеспечивалась прочность при больших внутренних давлениях.
Привычный способ уменьшения напряжений увеличением размеров в данном случае не достигает цели. Следовательно, для сосудов высокого давления необходимо искать какие-то новые конструктивные решения. В середине позапрошлого столетия академиком А.К. Гадолиным была создана теория расчета артиллерийских стволов, составляемых из нескольких сопрягаемых толстостенных цилиндров, чем обеспечивалась прочность при больших внутренних давлениях.
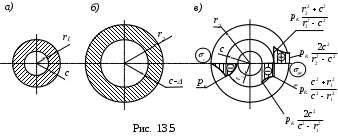
Положим, мы имеем два цилиндра (рис 13.5,а,б). Внутренний радиус первого цилиндра (рис 13.5,а) обозначим r1, а внешний с. У второго цилиндра (рис. 13.5,б) внутренний радиус на величину меньше наружного радиус первого цилиндра, т.е. равен с-. Внешний радиус второго цилиндра (рис 13.5,б) равен r2. После горячей посадки при остывании (рис 13.5,в) между цилиндрами возникает контактное давление рК. Определим его.
При посадке внешний радиус первого цилиндра сократится и точки цилиндра на контактной поверхности получат отрицательное смещение u1. Внутренний радиус внешнего цилиндра увеличится. Точки внутренний радиус внешнего цилиндра получит положительное смещение u2.
Составим условие совместности деформации
u2 – u1=(13.22)
Перемещение u1 определяется по формуле (13.11) или (13.20), если положить
p1=0, p2= pK, аr2 иrзаменить наc. Тогда получим
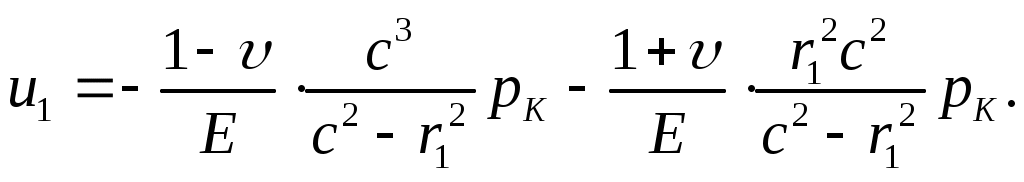
Перемещение u2 определяется по формуле (13.11). Для этого полагаем
p2=0, p= pK, r1= r=с;
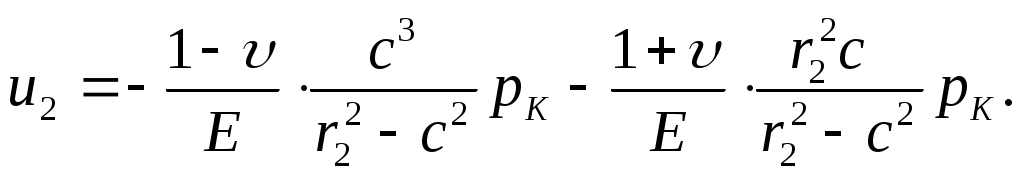
Тогда предполагая, что Е и для обоих цилиндров одинаковыми согласно выражению (22) определяем,
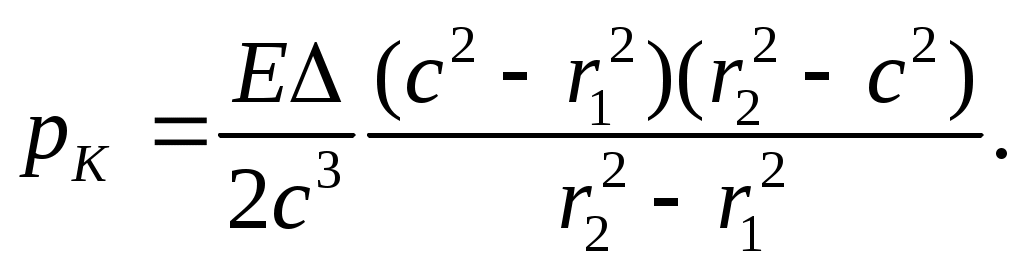 (13.23)
(13.23)
Картина распределения напряжений в сопряженных цилиндрах показана на рис. 13.5,в.
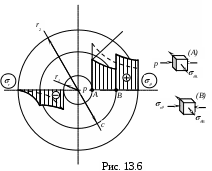
Если теперь составной цилиндр нагрузить внутренним давлением, то обе его части будут работать как одно целое и в составном цилиндре возникнут напряжения, определяемые формулой (13.15). Эти напряжения должны быть алгебраически просуммированы с предварительными напряжениями натяга (рис. 13.6.).
Из-за большого Е – контактное давление может быть весьма большим и при малых . Поэтому натяг требует дозировки и должен подбираться для заданного давления так, чтобы была обеспечена прочность не только внутреннего, но и внешнего цилиндра. Легко составить условие равнопрочности цилиндров (рис. 13. 6.):
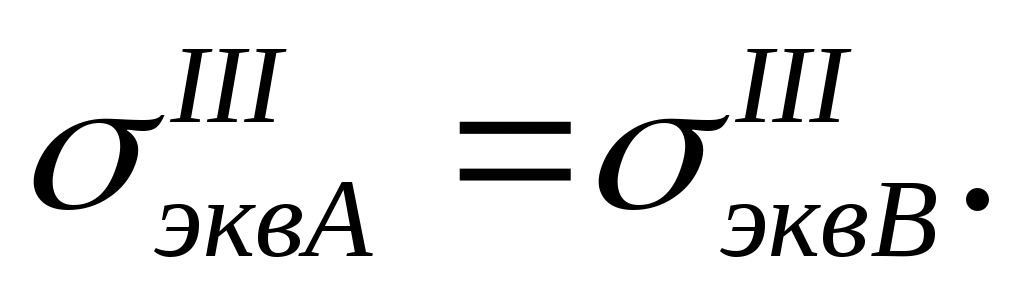
Согласно с формулой Ляме (10), получим:
в точке А

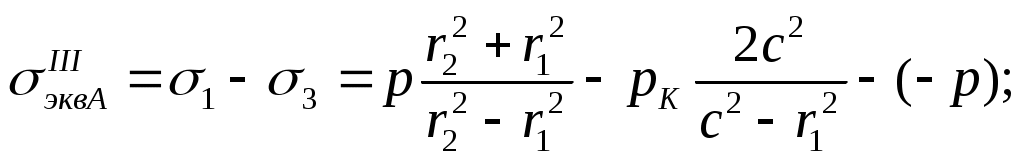 (13.24)
(13.24)
в точке B
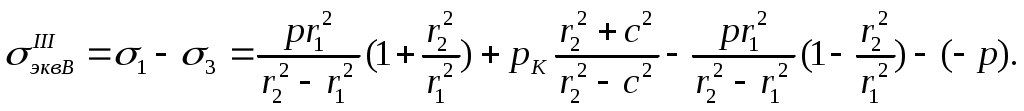 (13.25)
(13.25)
Если приравнять эти выражения, то получим
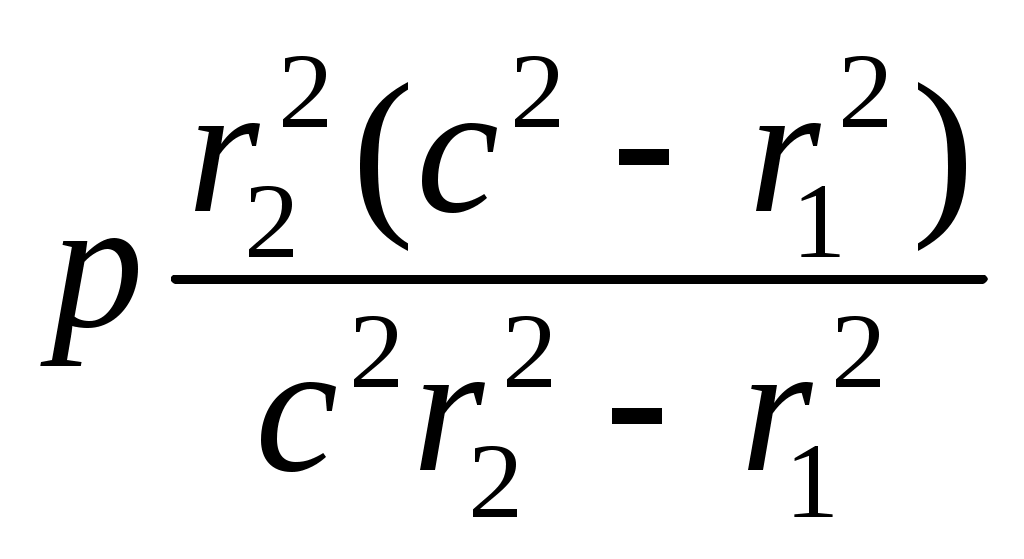
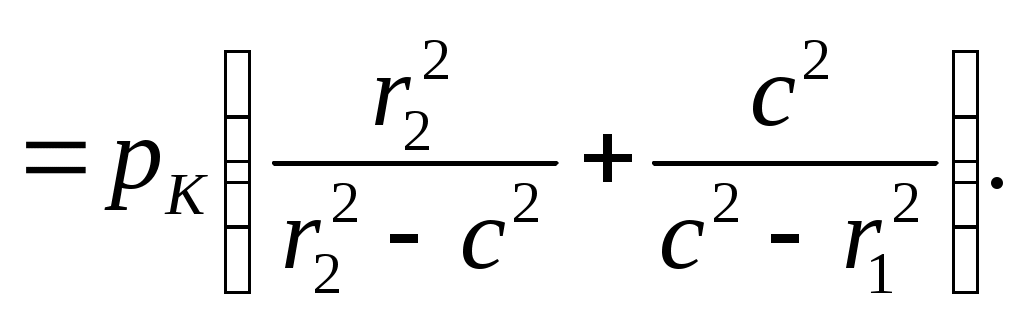 (13.26)
(13.26)
И тогда подставить рК из (13.23), найдём натяг , который обеспечивает условие равнопрочности при заданном рабочем давлении р:
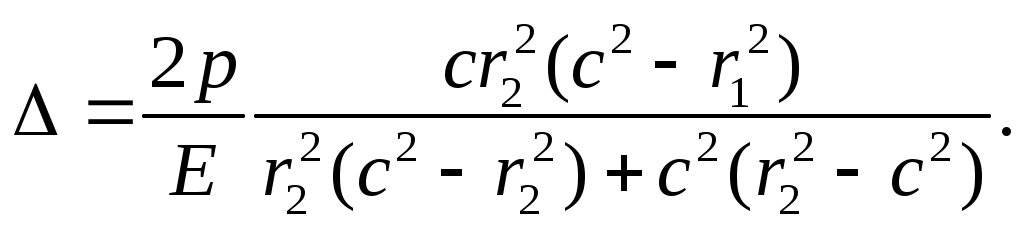 (13.27)
(13.27)
Если исключить из выражения (13.24) рК поставив (13.26), то получим
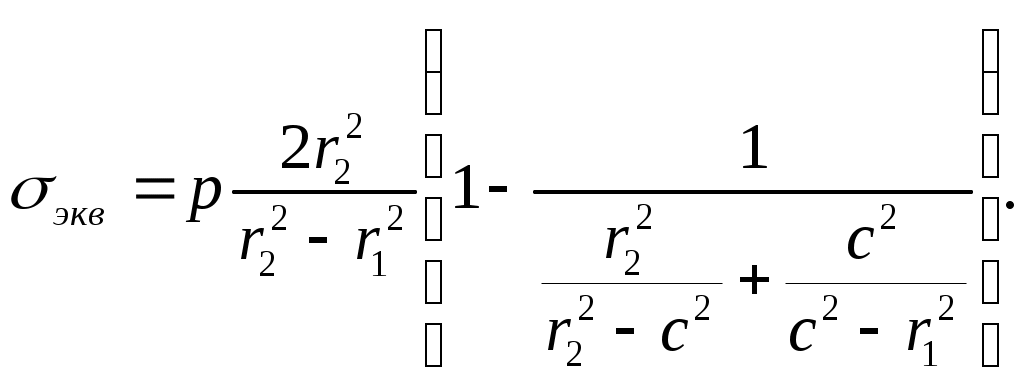
Условия r на внутренней и наружной поверхностях цилиндра (Г.У.).
Г.У. r=r1, r =-p1;
r=r2, r =-p2. (13.9)
Для определения постоянных А и В согласно (13.9) получим следующие два уравнения:
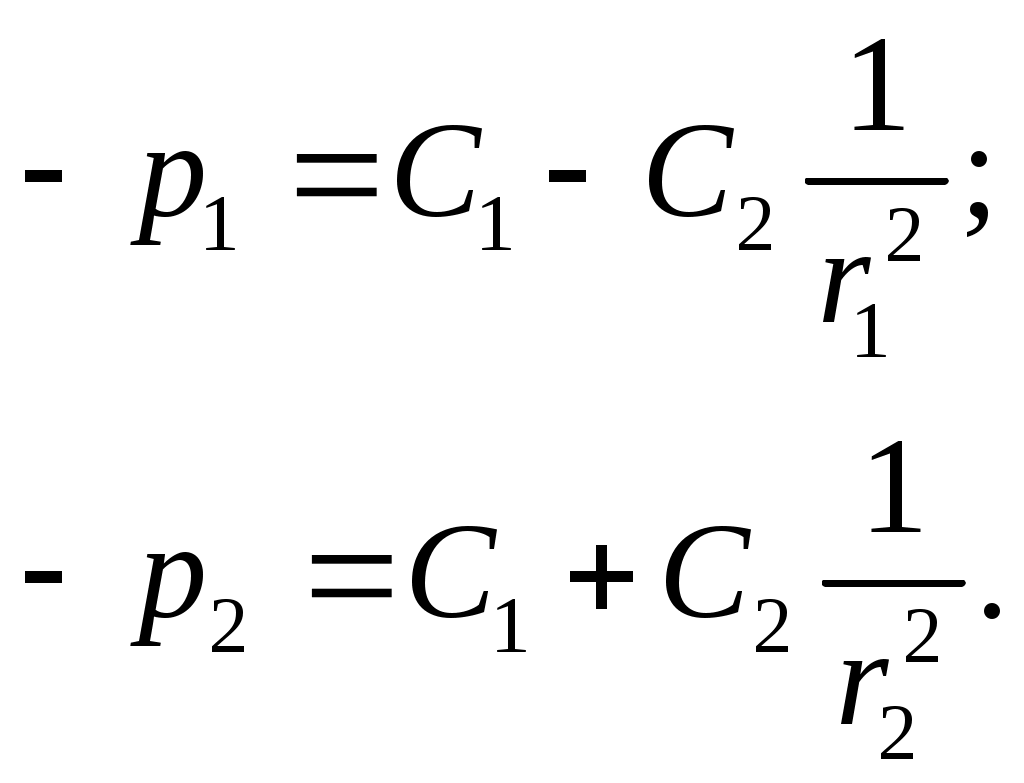
Решая эти уравнения относительно С1 и С2 , найдём :
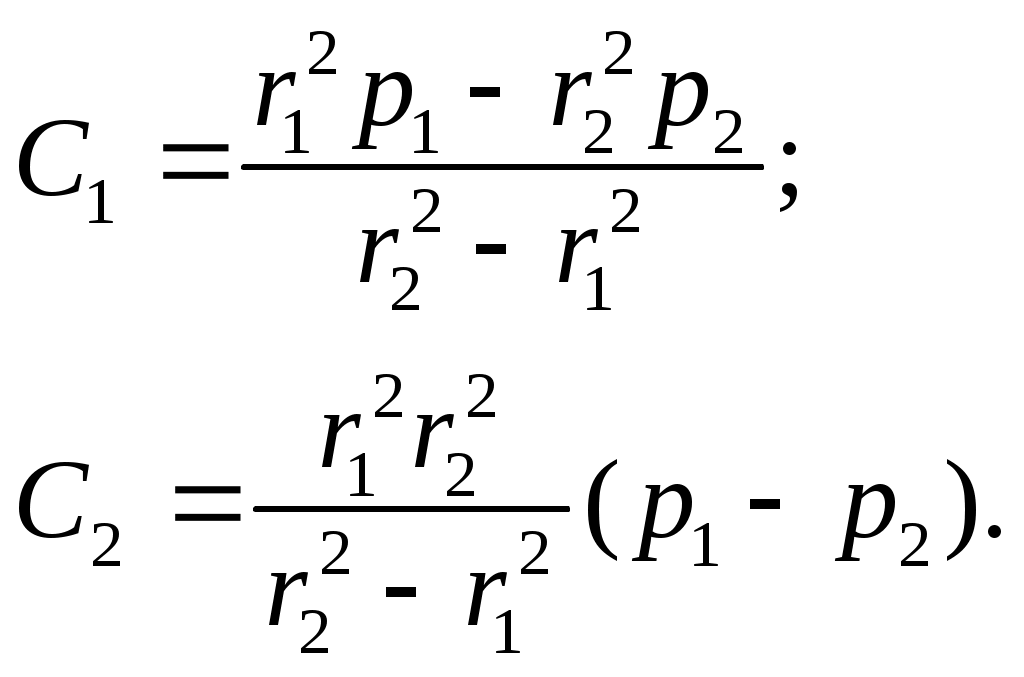
Подставляя значения постоянных в выражение (13.8), получим формулу для определения напряжений (формула Ляме)
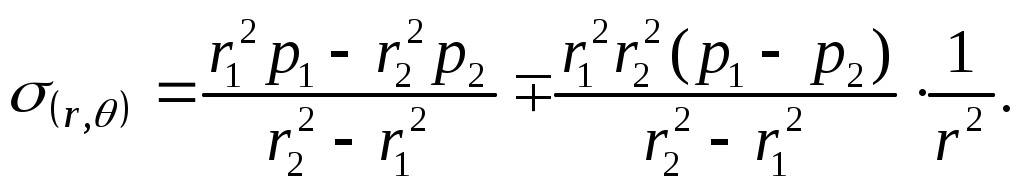 (13.10)
(13.10)Аналогично, через решение (13.6), представив напряжения по формуле (13.4) и используя Г.У. (13.9), получим формулу (формула Ляме) для определения радиального перемещения
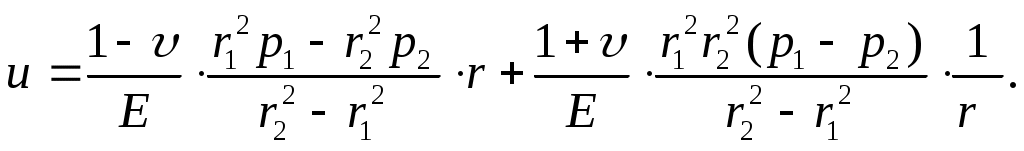 (13.11)
(13.11)Сложив rи (см.формулу (13.10)) , убеждаемся, что их сумма величина постоянная, т.е.
Относительная деформация рассматриваемого нами кольца в направлении, параллельном оси цилиндра, также будет постоянной на любом радиусе, т.е.
Н
 а основании этого цилиндр можно рассматривать как набранный из отдельных колец, нанизанных на ось. Поперечные сечения цилиндра при деформации остаются плоскими.
а основании этого цилиндр можно рассматривать как набранный из отдельных колец, нанизанных на ось. Поперечные сечения цилиндра при деформации остаются плоскими.При наличии днища, т.е. закрытой трубы, в поперечных сечениях возникают осевые напряжения Z(рис. 13.2). Допуская их равномерное распределение по толщине стенки (что допустимо вдали от днищ) и составляя уравнение равновесия всех сил на ось Z, получаем
или
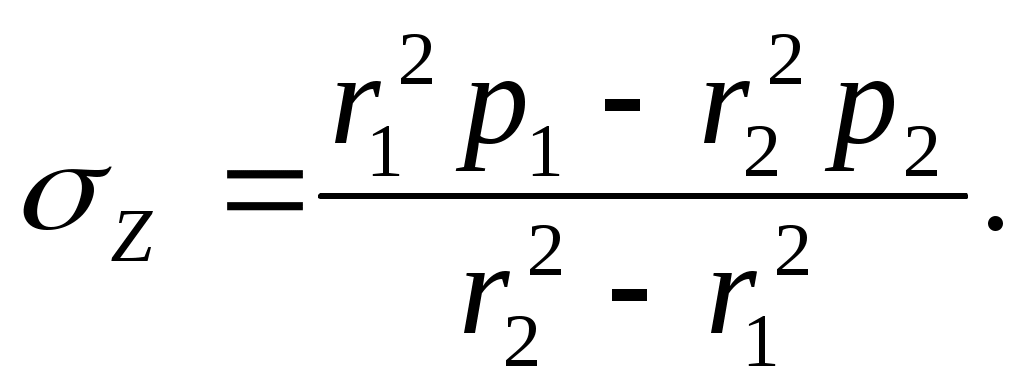
Сопоставление этой формулы с формулой Ляме (13.10) показывает, что главное осевое напряжение является средним арифметическим между окружным и радиальным
(13.14)
13.2. Определение напряжений и перемещений в толстостенном цилиндре
Рассмотрим два частных случая нагружения цилиндра (трубы).
1. Цилиндр (труба) нагружен только внутренним давлением.
В этом случае полагаем p1 = pи p2 = 0. Выражение (10) примет вид
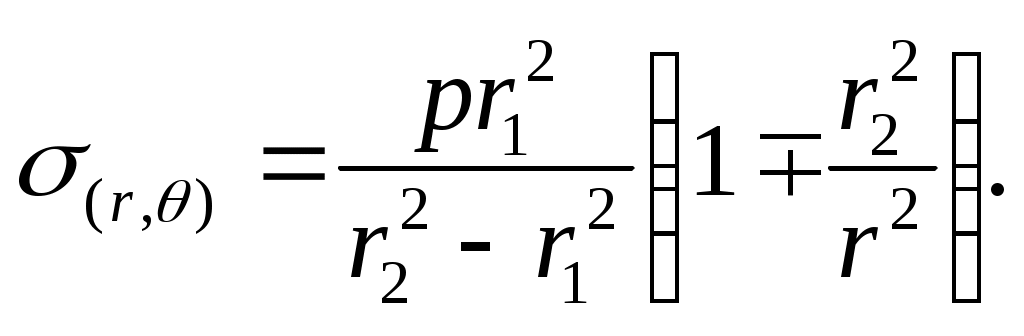
Н

а рис. 13.3 показаны эпюры изменения радиального и окружного напряжения по толщине цилиндра при нагружении внутренним давлением.
Наиболее нагруженным оказывается внутренний слой, для которого
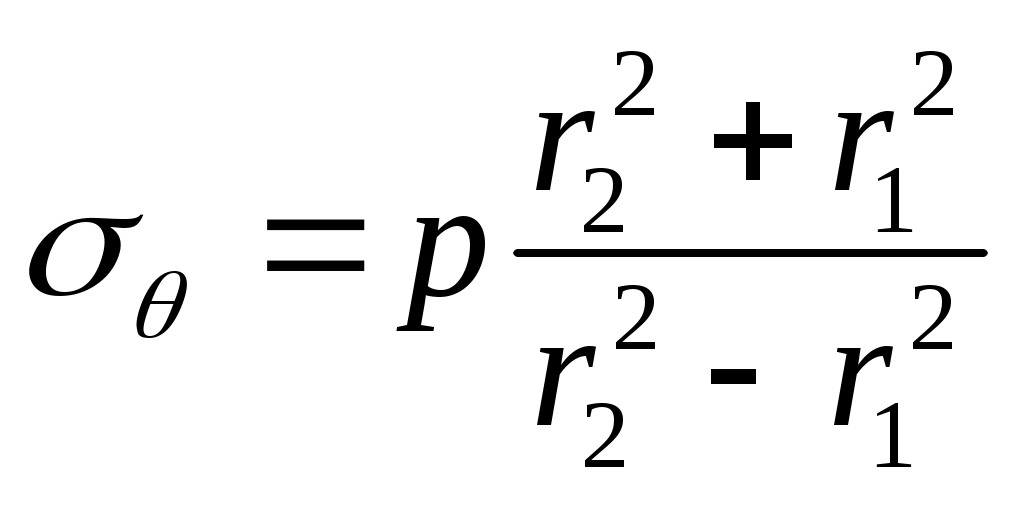 при r=r1,
при r=r1,В этом случае получаем по теории наибольших касательных напряжений
(в случае отсутствия осевой силы т.е. при Z=0)
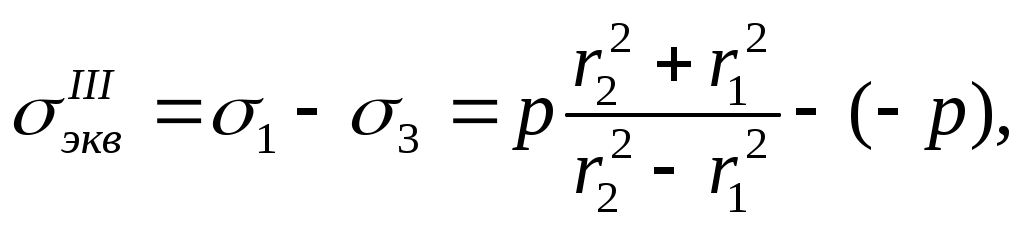
или
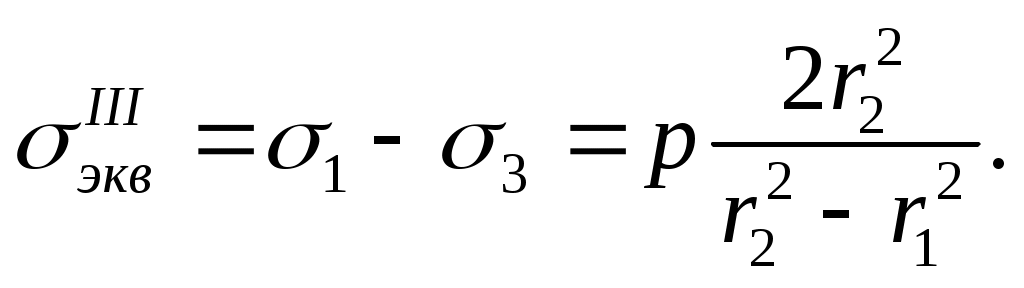 (13.16)
(13.16)Радиальное перемещение у внутренней поверхности (увеличение внутреннего радиуса)
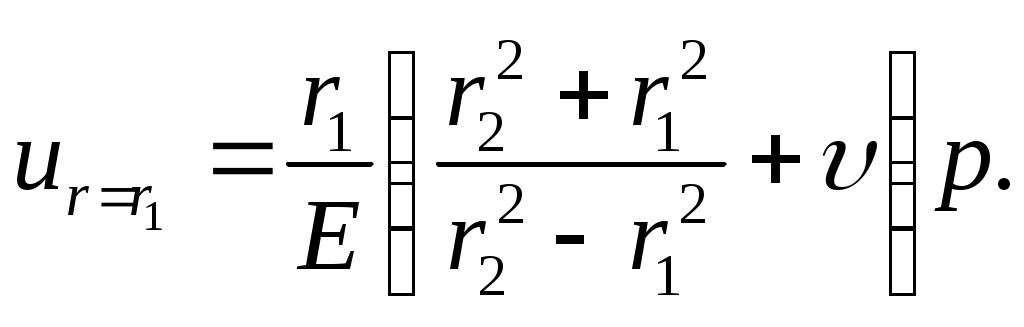 (13.17)
(13.17)Напряжения и перемещения у наружной поверхности цилиндра следующие:
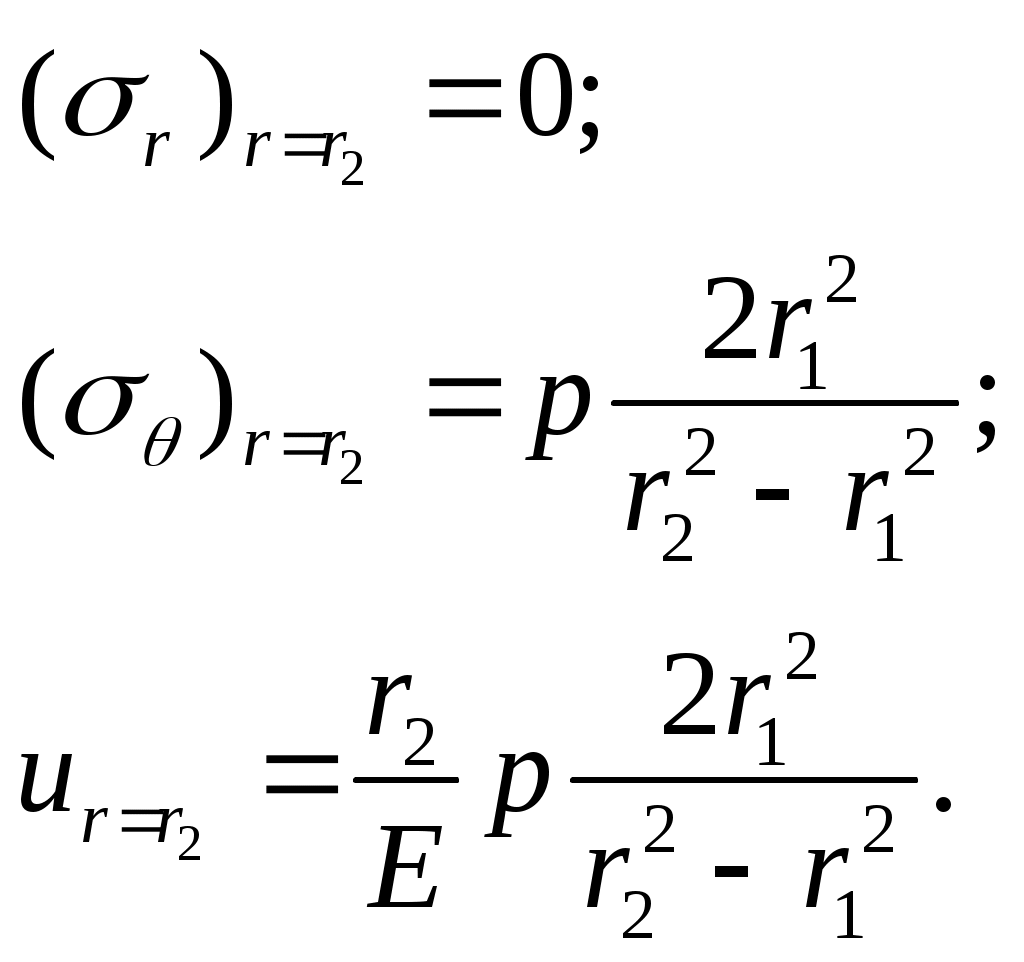 (13.18)
(13.18)Напряжения при
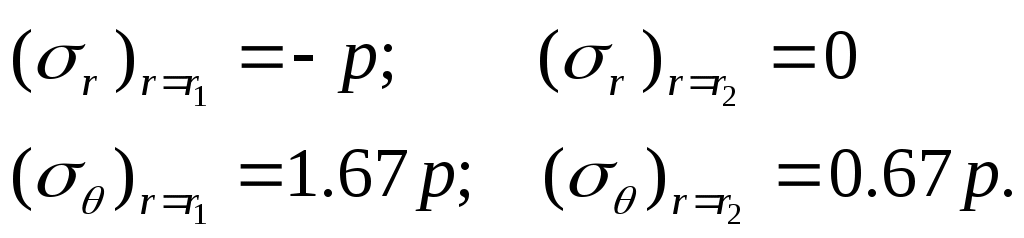
Если
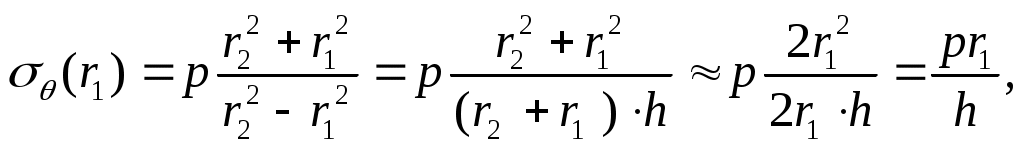
т.е.
Рассмотрим случай, когда,
т.е. когда цилиндр имеет бесконечно большую толщину. Тогда выражение (13.15) принимает вид
Это значит, что у цилиндра с бесконечно большой толщиной стенки при отсутствии осевых напряжений все точки находятся в состоянии чистого сдвига. Практически цилиндры с соотношением
Эквивалентное напряжение согласно (13.16) при
Е
 сли r2,
сли r2, 2. Цилиндр (труба) нагружен внешним давлением.
В этом случае полагаем p1 =0и p2 = p . Выражение (13.10) примет вид
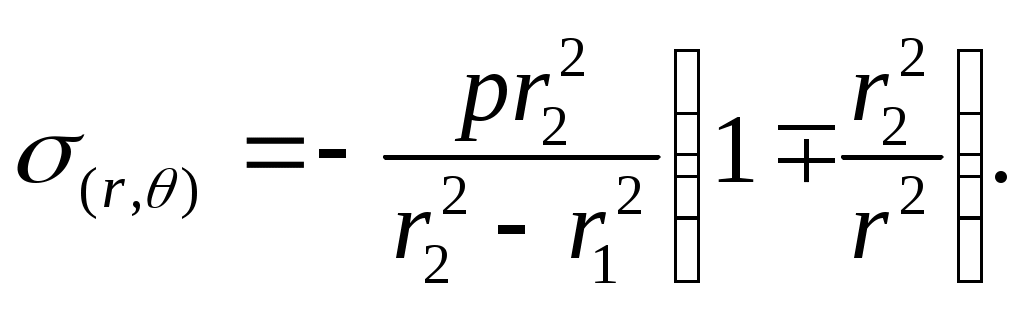 (13.19)
(13.19)Эпюры напряжений по толщине цилиндра для этого случая нагружения представлены
на рис. 13.4.
Напряжения при
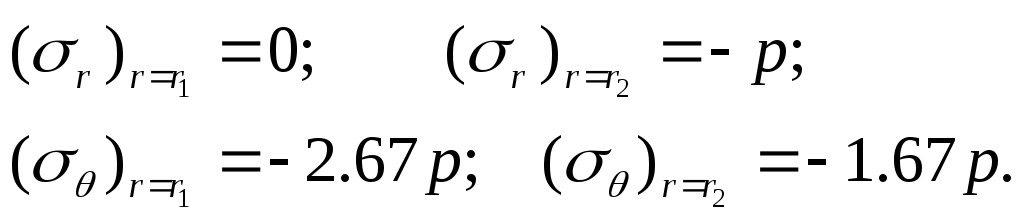
Наибольшее эквивалентное напряжение имеет место у внутренней поверхности цилиндра. При отсутствии осевой силы
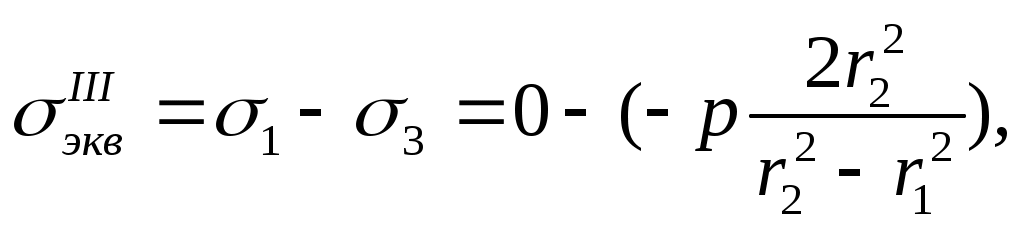
или

Это выражение совпадает с тем, которое было получено для случая внутреннего давления (смотри (13.16)) при r2,
Формула для перемещений примет следующий вид:
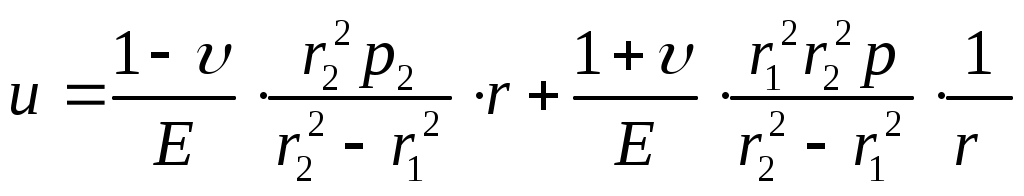 (13.20)
(13.20)Если r1 0 (r1 =0), тогдаr= =-р (т.е. имеем гидростатическое напряженное состояние).
Формула для перемещений примет вид:
13.3. Определение напряжений в составных трубах
Выше мы показали, что увеличение толщины не может во всех случаях обеспечить необходимой прочности трубы. В пределe при бесконечно большой толщине (
Положим, мы имеем два цилиндра (рис 13.5,а,б). Внутренний радиус первого цилиндра (рис 13.5,а) обозначим r1, а внешний с. У второго цилиндра (рис. 13.5,б) внутренний радиус на величину меньше наружного радиус первого цилиндра, т.е. равен с-. Внешний радиус второго цилиндра (рис 13.5,б) равен r2. После горячей посадки при остывании (рис 13.5,в) между цилиндрами возникает контактное давление рК. Определим его.

При посадке внешний радиус первого цилиндра сократится и точки цилиндра на контактной поверхности получат отрицательное смещение u1. Внутренний радиус внешнего цилиндра увеличится. Точки внутренний радиус внешнего цилиндра получит положительное смещение u2.
Составим условие совместности деформации
u2 – u1=(13.22)
Перемещение u1 определяется по формуле (13.11) или (13.20), если положить
p1=0, p2= pK, аr2 иrзаменить наc. Тогда получим
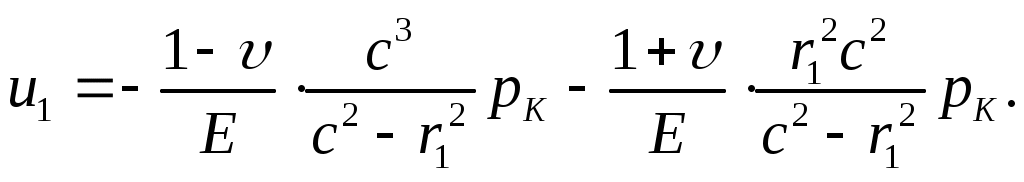
Перемещение u2 определяется по формуле (13.11). Для этого полагаем
p2=0, p= pK, r1= r=с;
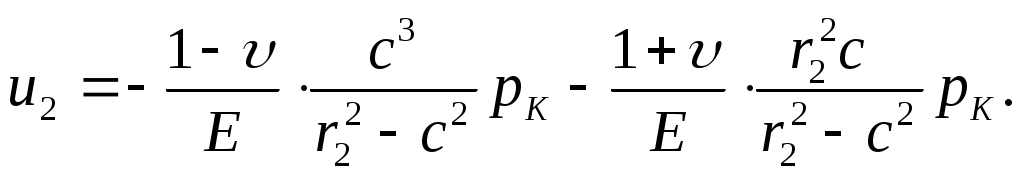
Тогда предполагая, что Е и для обоих цилиндров одинаковыми согласно выражению (22) определяем,
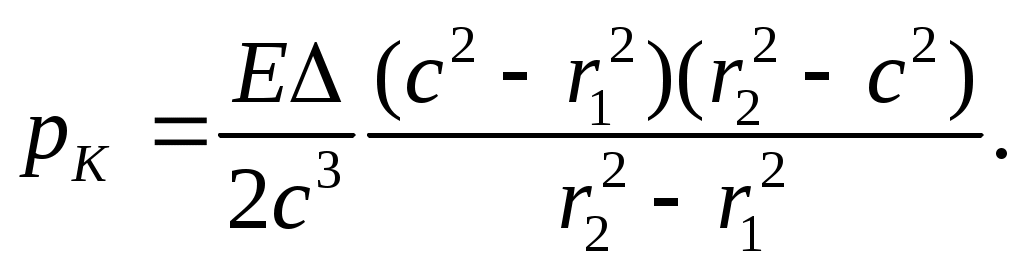 (13.23)
(13.23)Картина распределения напряжений в сопряженных цилиндрах показана на рис. 13.5,в.
Если теперь составной цилиндр нагрузить внутренним давлением, то обе его части будут работать как одно целое и в составном цилиндре возникнут напряжения, определяемые формулой (13.15). Эти напряжения должны быть алгебраически просуммированы с предварительными напряжениями натяга (рис. 13.6.).
Из-за большого Е – контактное давление может быть весьма большим и при малых . Поэтому натяг требует дозировки и должен подбираться для заданного давления так, чтобы была обеспечена прочность не только внутреннего, но и внешнего цилиндра. Легко составить условие равнопрочности цилиндров (рис. 13. 6.):

Согласно с формулой Ляме (10), получим:
в точке А
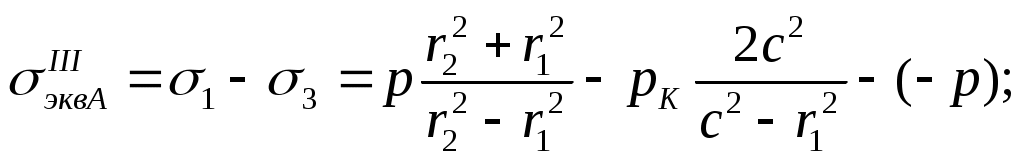 (13.24)
(13.24)в точке B
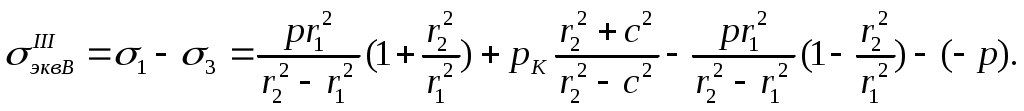 (13.25)
(13.25)Если приравнять эти выражения, то получим
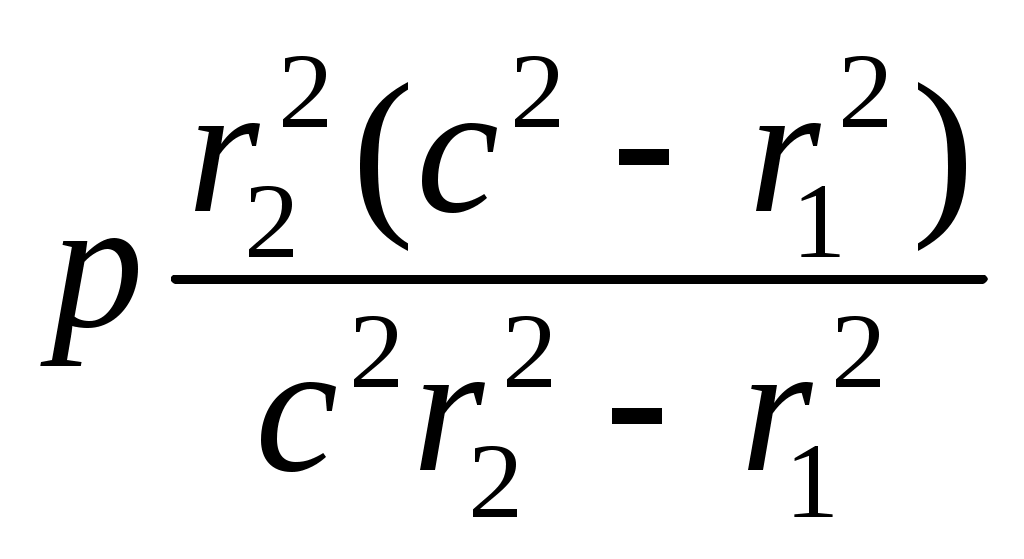
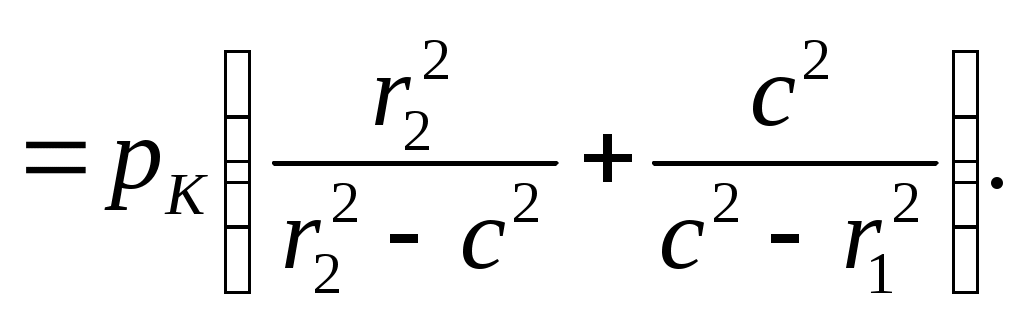 (13.26)
(13.26)И тогда подставить рК из (13.23), найдём натяг , который обеспечивает условие равнопрочности при заданном рабочем давлении р:
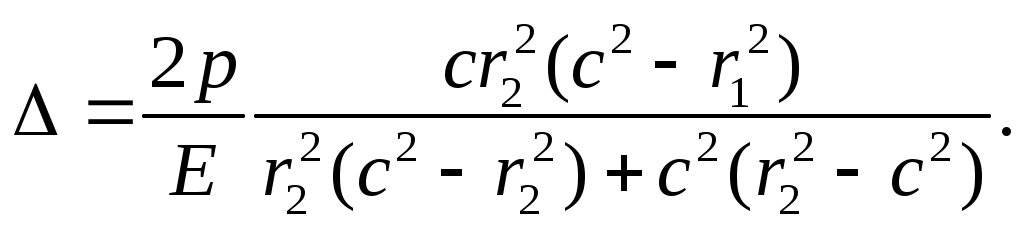 (13.27)
(13.27)Если исключить из выражения (13.24) рК поставив (13.26), то получим