Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 406

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Деформация, остающаяся в теле после разгрузки, получила названиеостаточной или пластичной, а способность тела приобретать пластическую деформацию – пластичность.

Сплошность

7.1.1. Общие замечания

Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу

Методика расчёта

Нагрузка, при которой прямолинейная форма перестаёт быть формой устойчивого равновесия, называется критической(Fкр ). Таким образом, исследование устойчивости стержня заключается в определении Fкр. Для обеспечения устойчивости допускаются нагрузки, составляющие лишь часть критических. Отношение критической нагрузки Fкр к её допускаемой величине ([F]y) называется коэффициентом устойчивости: (11.1)Коэффициент ny зависит от материала стержня. Его рекомендуемые величины находятся в пределах: для стальных стоек 1.5…3; для деревянных 2.5…3.5; для чугунных 4.5…5.5. Метод Эйлера для определения критической силы. Формула Эйлера.Для исследования устойчивости равновесия упругих систем имеется несколько методов: метод малых колебаний, энергетический метод и др. В инженерной практике для невесомых стержней с нагрузкой, приложенной точно в центре тяжести торцовых сечений и параллельно продольной оси стержня используют более простой метод – метод Эйлера.Метод Эйлера основан на анализе разветвления форм равновесия упругой системы. Следовательно, при критической силе наряду с исходной прямолинейной формой как бы возможна смежная, весьма близкая к ней искривленная форма. Для вывода формулы Эйлера рассмотрим шарнирно - опёртый, центрально - сжатый стержень постоянного сечения (рис. 11. 3) в слегка отклонённом состоянии от прямолинейной формы.Изгибающий момент в произвольном сечении равенF (11.2)Дифференциальное уравнение изгиба стержня запишется в виде: (11.3)или (11.4)где (11.5)Интеграл дифференциального уравнения (11.4) имеет вид (11.6)Для определения значений произвольных постоянных А и В используем граничные условия. Первое граничное условие: при z=0 и Следовательно, уравнение оси изогнутого бруса (6) примет вид (11.7)Таким образом, стержень изгибается по синусоиде.Второе граничное условие: при z=l и  Bsinkl=0Это условие выполняется в двух случаях:1) В=0; 2) sinkl=0Первый случай нас не интересует, так как при В=0 прогибы во всех точках равны нулю, следовательно, стержень остается прямым.Второе условие sinkl=0 дает kl= 2 3 nучтя значение k (11.5), получим: Итак, получено не одно, а множество значений критической силы. Каждой критической силе соответствует своя форма равновесия (рис. 11.4). Подставляя найденное значение k в уравнение оси изогнутого бруса (11.7), замечаем, что при первой критической силе стержень изгибается по одной полуволне синусоиды, а при всех последующих число полуволн равно номеру соответствующей критической силы. Равновесие, соответствующее первой форме изгиба, является устойчивым, а все всем остальным – неустойчивым.Для инженерных расчетов практический интерес представляет только наименьшая критическая сила (11.8)Эту формулу в 1744 г. впервые получил Леонард Эйлер, поэтому она называется формулой Эйлера, а определяемую этой формулой критическую силу – эйлеровой силой.Из формулы (11.8) видно, что величина критической силы прямо пропорциональна жесткости и обратно пропорциональна квадрату длины стержня.Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости материала, но совершенно не зависит от прочностных характеристик материала, из которого изготовлен стержень. Два стержня с одинаковыми геометрическими размерами, но изготовленные из различных сталей и работающие в упругой стадии, теряют устойчивость при одной и той же критической силе.Таким образом, выясняется резкая разница между работой стержня на растяжение и на сжатие. Предельная растягивающая сила непосредственно зависит от прочностных характеристик материала и поэтому различна для разных сортов стали, в то время как при сжатии в пределах упругости наблюдается совершенно иная картина. Предельная растягивающая сила не зависит от длины стержня, в то время как при сжатии она быстро падает с увеличением длины.Продольный изгиб сжатых стержней особенно опасен потому, что он наступает внезапно, и поэтому его трудно предупредить. В растянутых стержнях признаки опасного состояния часто наступают задолго до разрушения, а в сжатых стержнях каких- либо заметных признаков потери устойчивости, как правило, установить не удается.11.3. Влияние способов закрепления концов стержня на величинукритической силыНа рис. 11.5 показаны различные случаи закрепления концов сжатого стержня. Для каждого случая необходимо проводить свое решение аналогичное тому, что сделано в предыдущем параграфе для шарнирно опертого стержня. Эти решения показывают, что для всех случаев, изображенных на рис. 11.5, критическую силу можно представить в виде формулы: (11.9)где   коэффициент приведения длины, а величина ll0называется приведенной (свободной) длиной. Понятие о приведенной длине было впервые введено профессором Петербургского института путей сообщения Ф.С. Ясинским (1892).Свободная длина l0может быть истолкована как некоторая условная длина шарнирно опертого стержня, имеющего такую же критическую силу, как заданный стержень. В отдельных случаях это положение вытекает из чисто геометрического толкования (длина полуволны синусоды). Так, например, если стержень заделан одним концом, рассматривать как половину стержня, шарнирно опертого по концам, то l0= 2l. Следовательно, =2.Для стержня, заделанного двумя концами, длина полуволны, замеренная между двумя точками перегиба, где Мх=0,составит половину длины стержня, следовательно, для этого случая =0,5. 11.4. Пределы применимости формулы Эйлера. Формула Ясинского Формула Эйлера, полученная более 267 лет назад, долгое время являлась предметом дискуссий. Формула Эйлера для некоторых случаев не подтверждалась экспериментами. Объясняется это тем, что формула Эйлера выводилась в предположении, что при любом значении силы стержень работает в пределах упругих деформаций с использованием закона Гука. По этому формулу Эйлера нельзя применять в случаях, когда критические напряжения больше предела пропорциональности. Для установления предела применимости формулы Эйлера найдем Здесь радиус инерции. Обозначим через  Величина  называется гибкостью стержня.Итак, (11.10) Это так же формула Эйлера, но записанная для критического напряжения, а не для критической силы. Принято изображать уравнение (11.10) в координатах кр -(рис. 11.6). Полученную кривую часто называют гиперболой Эйлера. Как видно из уравнения (11.10), при малых гибкостях критические напряжения могут значительно превосходить предел прочности материала. Действительно короткие и толстые стержни (например, кубы, имеющие гибкость 

Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.

Так как

Отсюда определяется меридиональное напряжение т.

Напряженное состояние является двухосным

Из формулы Лапласа находим

где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки

15. Динамическое действие нагрузок

15. Динамическое действие нагрузок…………………………………..216



откуда

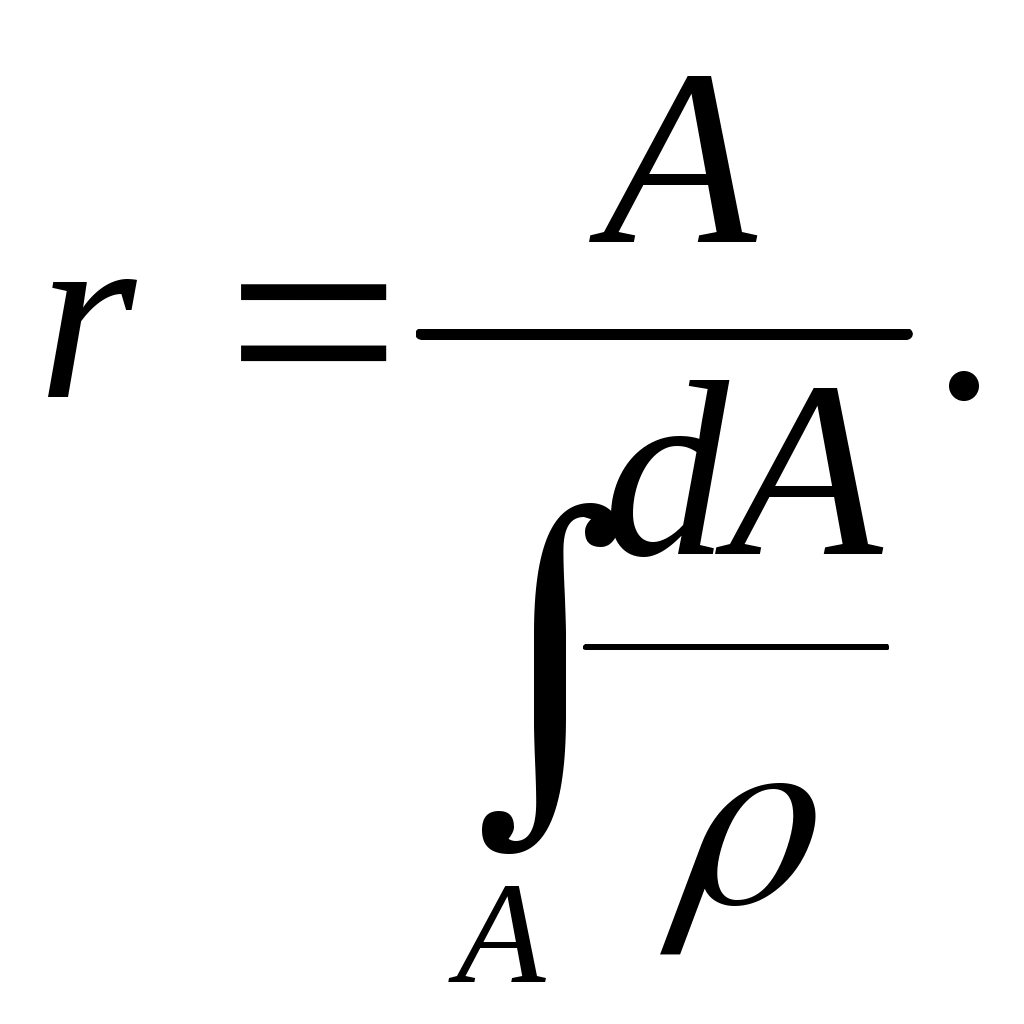(14.11)

Рассмотри стержень с прямоугольным сечением (рис. 14.6). Для него

,

тогда



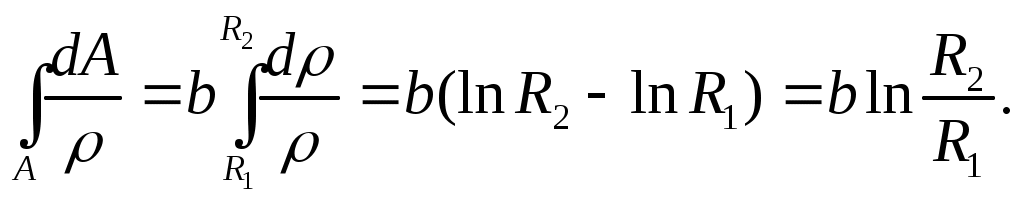
Следовательно,

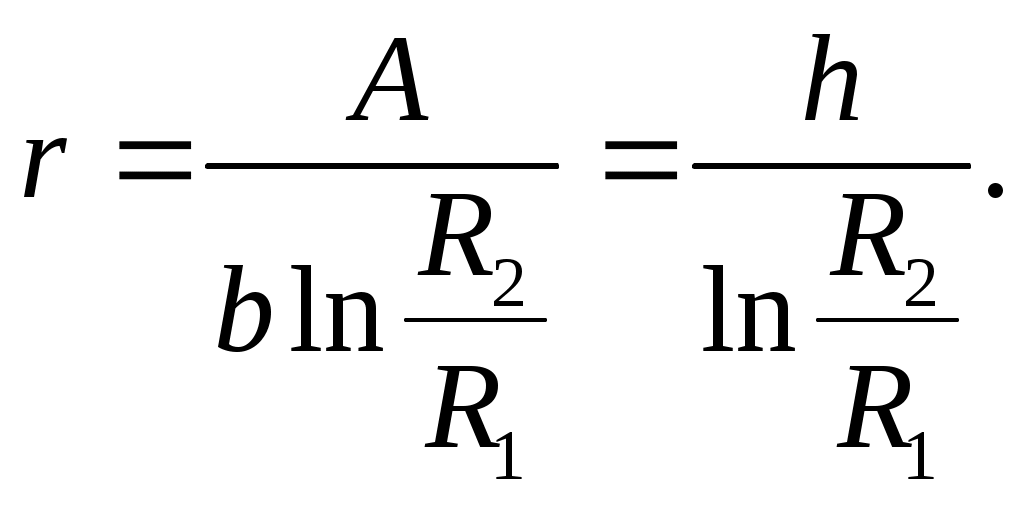(14.12)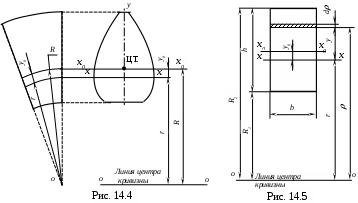




Во многих случаях определение положения нейтральной оси (х-х) можно произвести приближенно. Используем формулу (14.9)



но, с другой стороны (см. формулу (14.6)), имеем



Приравнивая эти два выражения, находим



Для приближённого решения можно положить



следовательно,

(14.13)

Так, например, для прямоугольного сечения получим



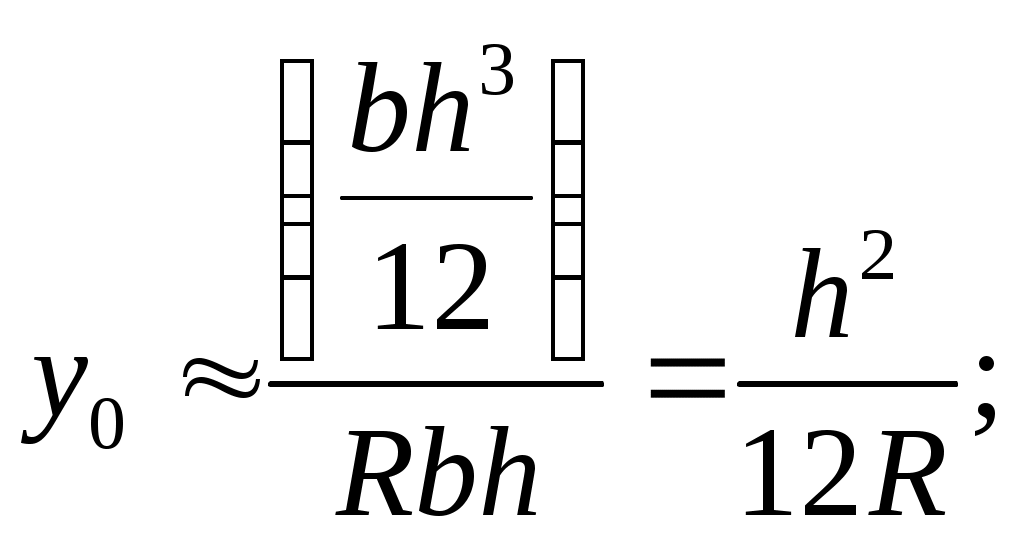
для круглого сечения



Приближенные формулы (см. таблицу 1) дают хорошую точность для брусьев средней кривизны, когда

Таблица1

ТИП СЕЧЕНИЯ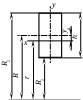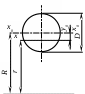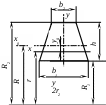










Точное

решение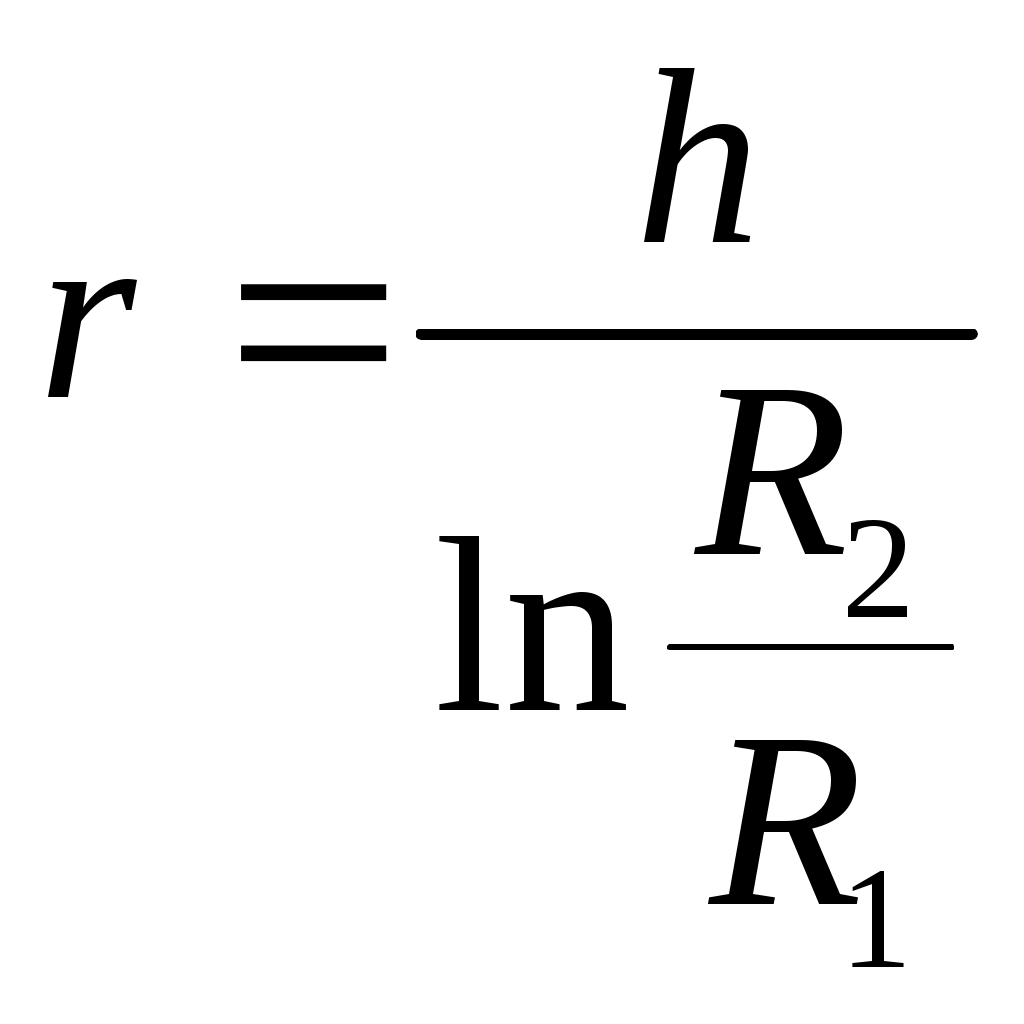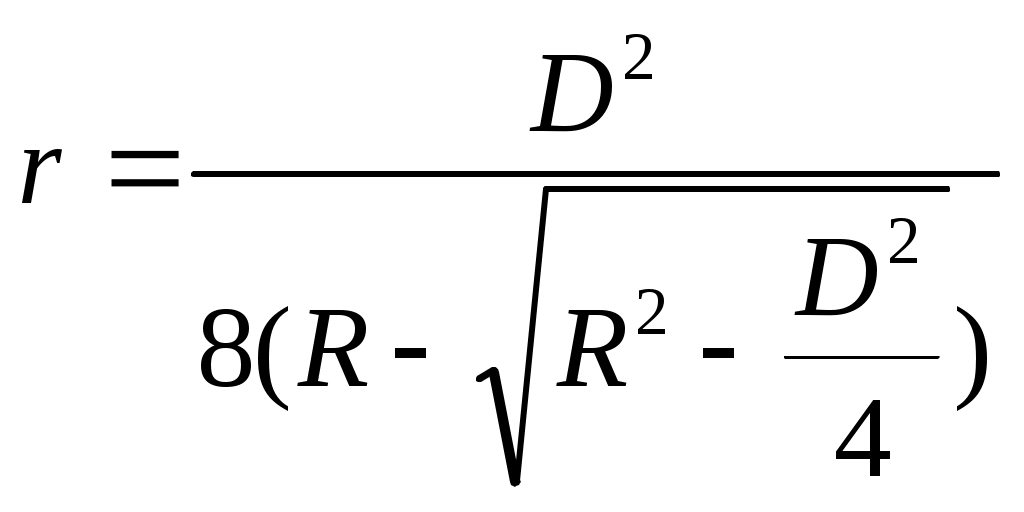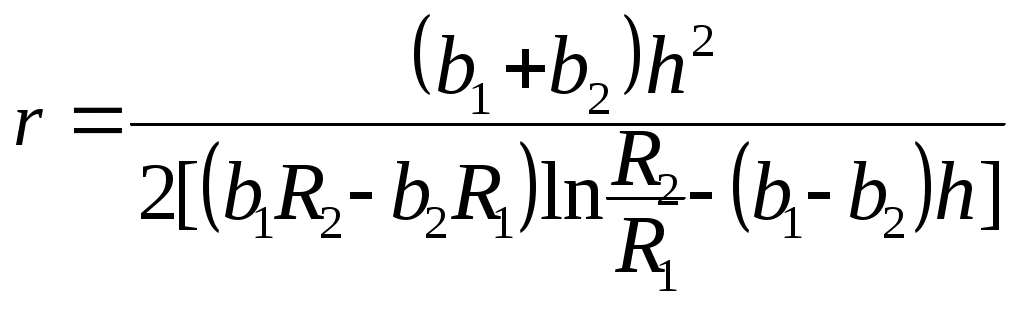














Приближенное решение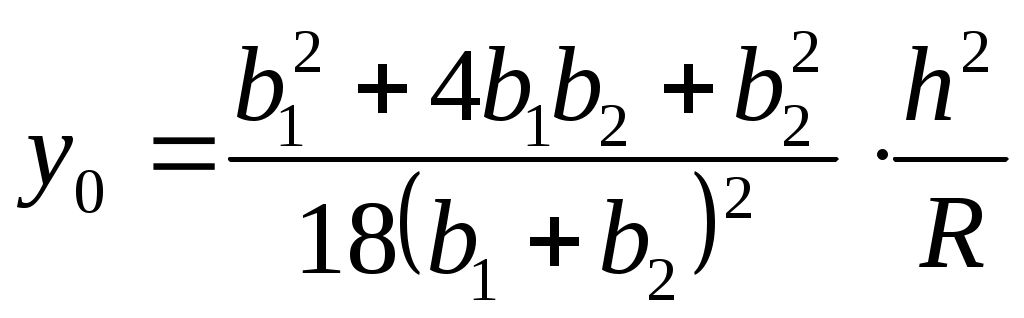











14.5. Напряжения при одновременном действии продольной силы и изгибающего момента
Если в поперечном сечении кривого бруса одновременно возникают изгибающий момент и продольная сила, то напряжения следует определять как сумму напряжений от двух указанных воздействий:
(14.14)

В этой формуле величина изгибающего момента должна быть найдена относительно оси, проходящей через центр тяжести сечения, т.к. напряжения от продольной силы N/A определяются из условия, что нормальная сила приложена в центре тяжести поперечного сечения.

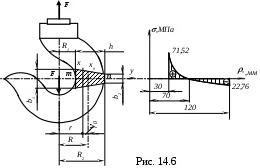
П р и м е р. Проверить прочность крюка в сечении m-m (трапеция) по нормальному напряжению (рис. 14.6) при следующих данных: F=23 кН; R1=3 cм; R2=12 cм; b1=4 cм; b2=2 cм; [] =90 МПа.




Расстояние от центра кривизны до центра тяжести



Радиус кривизны нейтрального слоя



Величина смещения нейтрального слоя относительно центра тяжести



площадь сечения



статический момент сечения относительно нейтральной оси



Координаты крайних точек сечения:



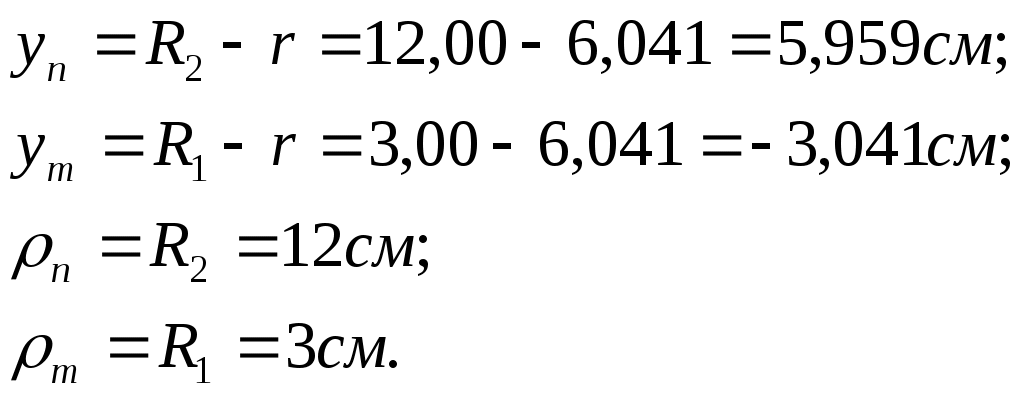
Нормальная сила и изгибающий момент в сечении равны:



По формуле (14.14) находим напряжения в крайних волокнах

Эпюра от совместного действия нормальной силы и изгибающего момента показана на рис. 14.6. Она убедительно показывает, что для расчета кривых брусьев нельзя пользоваться формулами, полученными для прямого бруса.

Практика показала, что кривые брусья можно разделить на две группы:


брусья малой кривизны и брусья большой кривизны

Для определения напряжений в брусья малой кривизны приближенно можно пользоваться формулами прямого бруса.

В таблице 2 представлено влияние кривизны на погрешность в напряжениях в кривом брусе, подсчитываемые по формулам для прямого бруса.
Таблица 2
Брусья большой кривизны
Брусья малой кривизны

R/h
2
3
5
8
10


 ,%
18,2
11,8
6,9
4,8
3,4
0



Из этой таблицы видно, что при R/h>5 допустимо определять напряжения по формулам для прямого бруса.
Вопросы для самопроверки

  1. Какие силовые факторы действуют в произвольном сечении кривого бруса?

  2. Как определяется положение нейтральной линии?

  3. По какому закону распределяются напряжения в сечении при чистом изгибе кривого бруса?

  4. По какой формуле можно приближённо вычислить радиус кривизны нейтрального слоя?

  5. Какие кривые брусья имеют большую кривизну и какие малую?

6. При каких отношениях R/hрасчетах на прочностьможно определять напряжения по формулам для прямого бруса.

15. Динамическое действие нагрузок


    1. Общие замечания

Во всех предыдущих курсах рассматривалось действие статической нагрузки, которая прикладывается к конструкции настолько медленно, что возникающие при этом ускорения движения частей конструкции весьма малы и поэтому их можно не учитывать.

Часто в инженерной практике встречаются так называемые динамические нагрузки, которые сравнительно быстро меняются по величине, месту приложения и по направлению. Поэтому при расчете необходимо учитывать силы инерции, зависящие как от массы конструкции, так и о массы нагрузок.

С силами инерции в свою очередь связаны дополнительные напряжения и деформации. Иногда они весьма велики и могу даже превышать напряжения и деформации от основных сил.

Общим приемом решения всех задач, связанных с учетом сил инерции, является принцип Д'Aламбера: необходимо приложить ко всем массам, движущимся с ускорением, помимо заданных и реактивных, также и силы инерции и после этого определить все силовые факторы в различных сечениях конструкции, используя уравнения равновесия статики.

На практике влияние динамической нагрузки, как правило, учитывается с помощью так называемого динамического коэффициента. Для получения максимального значения усилия динамическая нагрузка заменяется статической, а найденное от неё усилие или перемещение помножается на динамический коэффициент:

SД = kДSСТ. (15.1)

Динамический коэффициент kДво многих случаях определяют аналитически, а тех случаях, когда это сделать трудно, - экспериментально.

15.2. Учет сил инерции

15.2.1. Поступательное движение.

Рассмотрим расчет троса при подъёме груза весом Gc ускорением а. Вес 1м троса обозначим q. Если груз неподвижен, то в произвольном сечении каната mnвозникает статическое усилие от груза и каната:
NСТ =G
+qz.
При подъёме груза с ускорение а для определения натяжения каната воспользуемся принципом Д'Aламбера. В нашей задаче, суммарная сила инерции равна



где g – ускорение свободного падения.

Полное значение усилия NД определяется равенством (рис.15.1)


или



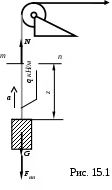
Динамическое напряжение равно



Величина динамического коэффициента

(15.2)

Если груз опускается то ускорение (-а).

При свободном падении ускорение (a=-g).

Канат следует за падающим грузом без натяжения

15.2.2. Вращательное движение
Расчёт обода маховика. В первом приближении обод маховика можно рассматривать как кольцо, вращающееся равномерно вокруг неподвижной оси O с угловой скоростью . При сделанных допущениях кольцо будет загружено равномерно распределённой по окружности инерционной нагрузкой qИН=q.

Если поперечное сечение имеет площадь А, удельный вес , то элементарная сила инерции

dFин=dman= (g)ARd2R=(g)Adv2,

где v– окружная скорость осевой линии кольца.

Из симметрии кольца и нагрузки qИН=qотносительно осиОследует, что во всех сечениях кольца возникают только продольные силы N и что эти силы одинаковы. Для определения значения силы N рассмотрим равновесие четверти кольца, показанного на рис. 15.2 сечением mn.



Смотрите также файлы