Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 396

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Деформация, остающаяся в теле после разгрузки, получила названиеостаточной или пластичной, а способность тела приобретать пластическую деформацию – пластичность.

Сплошность

7.1.1. Общие замечания

Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу

Методика расчёта

Нагрузка, при которой прямолинейная форма перестаёт быть формой устойчивого равновесия, называется критической(Fкр ). Таким образом, исследование устойчивости стержня заключается в определении Fкр. Для обеспечения устойчивости допускаются нагрузки, составляющие лишь часть критических. Отношение критической нагрузки Fкр к её допускаемой величине ([F]y) называется коэффициентом устойчивости: (11.1)Коэффициент ny зависит от материала стержня. Его рекомендуемые величины находятся в пределах: для стальных стоек 1.5…3; для деревянных 2.5…3.5; для чугунных 4.5…5.5. Метод Эйлера для определения критической силы. Формула Эйлера.Для исследования устойчивости равновесия упругих систем имеется несколько методов: метод малых колебаний, энергетический метод и др. В инженерной практике для невесомых стержней с нагрузкой, приложенной точно в центре тяжести торцовых сечений и параллельно продольной оси стержня используют более простой метод – метод Эйлера.Метод Эйлера основан на анализе разветвления форм равновесия упругой системы. Следовательно, при критической силе наряду с исходной прямолинейной формой как бы возможна смежная, весьма близкая к ней искривленная форма. Для вывода формулы Эйлера рассмотрим шарнирно - опёртый, центрально - сжатый стержень постоянного сечения (рис. 11. 3) в слегка отклонённом состоянии от прямолинейной формы.Изгибающий момент в произвольном сечении равенF (11.2)Дифференциальное уравнение изгиба стержня запишется в виде: (11.3)или (11.4)где (11.5)Интеграл дифференциального уравнения (11.4) имеет вид (11.6)Для определения значений произвольных постоянных А и В используем граничные условия. Первое граничное условие: при z=0 и Следовательно, уравнение оси изогнутого бруса (6) примет вид (11.7)Таким образом, стержень изгибается по синусоиде.Второе граничное условие: при z=l и  Bsinkl=0Это условие выполняется в двух случаях:1) В=0; 2) sinkl=0Первый случай нас не интересует, так как при В=0 прогибы во всех точках равны нулю, следовательно, стержень остается прямым.Второе условие sinkl=0 дает kl= 2 3 nучтя значение k (11.5), получим: Итак, получено не одно, а множество значений критической силы. Каждой критической силе соответствует своя форма равновесия (рис. 11.4). Подставляя найденное значение k в уравнение оси изогнутого бруса (11.7), замечаем, что при первой критической силе стержень изгибается по одной полуволне синусоиды, а при всех последующих число полуволн равно номеру соответствующей критической силы. Равновесие, соответствующее первой форме изгиба, является устойчивым, а все всем остальным – неустойчивым.Для инженерных расчетов практический интерес представляет только наименьшая критическая сила (11.8)Эту формулу в 1744 г. впервые получил Леонард Эйлер, поэтому она называется формулой Эйлера, а определяемую этой формулой критическую силу – эйлеровой силой.Из формулы (11.8) видно, что величина критической силы прямо пропорциональна жесткости и обратно пропорциональна квадрату длины стержня.Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости материала, но совершенно не зависит от прочностных характеристик материала, из которого изготовлен стержень. Два стержня с одинаковыми геометрическими размерами, но изготовленные из различных сталей и работающие в упругой стадии, теряют устойчивость при одной и той же критической силе.Таким образом, выясняется резкая разница между работой стержня на растяжение и на сжатие. Предельная растягивающая сила непосредственно зависит от прочностных характеристик материала и поэтому различна для разных сортов стали, в то время как при сжатии в пределах упругости наблюдается совершенно иная картина. Предельная растягивающая сила не зависит от длины стержня, в то время как при сжатии она быстро падает с увеличением длины.Продольный изгиб сжатых стержней особенно опасен потому, что он наступает внезапно, и поэтому его трудно предупредить. В растянутых стержнях признаки опасного состояния часто наступают задолго до разрушения, а в сжатых стержнях каких- либо заметных признаков потери устойчивости, как правило, установить не удается.11.3. Влияние способов закрепления концов стержня на величинукритической силыНа рис. 11.5 показаны различные случаи закрепления концов сжатого стержня. Для каждого случая необходимо проводить свое решение аналогичное тому, что сделано в предыдущем параграфе для шарнирно опертого стержня. Эти решения показывают, что для всех случаев, изображенных на рис. 11.5, критическую силу можно представить в виде формулы: (11.9)где   коэффициент приведения длины, а величина ll0называется приведенной (свободной) длиной. Понятие о приведенной длине было впервые введено профессором Петербургского института путей сообщения Ф.С. Ясинским (1892).Свободная длина l0может быть истолкована как некоторая условная длина шарнирно опертого стержня, имеющего такую же критическую силу, как заданный стержень. В отдельных случаях это положение вытекает из чисто геометрического толкования (длина полуволны синусоды). Так, например, если стержень заделан одним концом, рассматривать как половину стержня, шарнирно опертого по концам, то l0= 2l. Следовательно, =2.Для стержня, заделанного двумя концами, длина полуволны, замеренная между двумя точками перегиба, где Мх=0,составит половину длины стержня, следовательно, для этого случая =0,5. 11.4. Пределы применимости формулы Эйлера. Формула Ясинского Формула Эйлера, полученная более 267 лет назад, долгое время являлась предметом дискуссий. Формула Эйлера для некоторых случаев не подтверждалась экспериментами. Объясняется это тем, что формула Эйлера выводилась в предположении, что при любом значении силы стержень работает в пределах упругих деформаций с использованием закона Гука. По этому формулу Эйлера нельзя применять в случаях, когда критические напряжения больше предела пропорциональности. Для установления предела применимости формулы Эйлера найдем Здесь радиус инерции. Обозначим через  Величина  называется гибкостью стержня.Итак, (11.10) Это так же формула Эйлера, но записанная для критического напряжения, а не для критической силы. Принято изображать уравнение (11.10) в координатах кр -(рис. 11.6). Полученную кривую часто называют гиперболой Эйлера. Как видно из уравнения (11.10), при малых гибкостях критические напряжения могут значительно превосходить предел прочности материала. Действительно короткие и толстые стержни (например, кубы, имеющие гибкость 

Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.

Так как

Отсюда определяется меридиональное напряжение т.

Напряженное состояние является двухосным

Из формулы Лапласа находим

где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки

15. Динамическое действие нагрузок

15. Динамическое действие нагрузок…………………………………..216



Эта величина имеет минимум при

(13.28)

Полученное соотношение носит название условия Гадолина.

Сопоставляя выражения (13.16) и (13.28), мы видим, что посадка труб приводит к заметному снижению эквивалентного напряжения. Рассмотрим отношение выражений по этим формулам:



Если внутренний радиус r1будет малым, то посадка труб по соотношениям Гадолина дает почти двукратное снижение эквивалентного напряжения. Для тонкостенных труб, т.е. при r1r2 , посадка труб не дает эффекта.

В технике высоких давлений, кроме посадки, применяют так называемое автофретирование.

Автофретирование – это загрузка внутренним давлением с таким расчетом, чтобы во внутренних слоях возникли пластические деформации. После снятия этого предварительного давления сохраняется система остаточных упругих напряжений.

Во внешних слоях они растягивающие, а во внутренних – сжимающие, т.е. соблюдается принцип составных труб с натягом.

В дальнейшем при нагрузке давлением остаточные упругие напряжения суммируются с рабочими так, что во внутренних слоях имеет место частичная разгрузка.

Вопросы для самопроверки

    1. Какие трубы считаются толстостенными?

    2. Дифференциальное уравнение равновесия элемента трубы.

    3. Как получить формулу Ляме?

    4. Какая основная идея лежит в основе изготовления составных труб?

    5. Что такое натяг?

    6. Что такое автофретирование?



14. Расчёт кривого бруса

14.1. Постановка задачи. Основные допущения

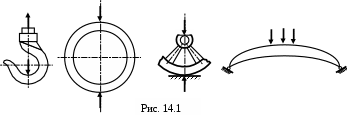
В инженерной практике часто встречаются стержни, ось которых является плоской или пространственной кривой, а сечения по длине стержня - переменно. На рис. 14.1 показаны примеры кривых брусьев: крюк подъёмного крана, замкнутое кольцо, обод колеса, несущий брус арочного моста. В общем случае решение такой задачи представляет большие трудности. Поэтому ограничимся рассмотрением таких брусьев у которых:



  1. ось бруса – плоская кривая;

  2. его поперечное сечение имеет ось симметрии, лежащую в плоскости кривизны бруса;

  3. все нагрузки действуют в плоскости кривизны бруса, являющейся при сделанных ограничениях плоскостью его симметрии.

При таких условиях все внутренние силы в произвольном сечении кривого бруса приводятся к трем компонентам: нормальной силе N, изгибающему моменту MXи поперечной силе QY.

Определение значений N, MX и QY выполняется, как обычно, с помощью метода сечений (РОЗУ). При этом изгибающий момент, так же как и в прямом брусе, подсчитывается относительно оси, проходящей через центр тяжести поперечного сечения.

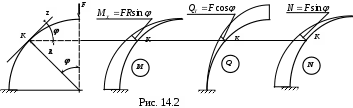
На рис. 14.2 показан брус, заделанный одним концом, ось которого очерчена по дуге окружности. На этом же рисунке показаны эпюры N, MX и QY от действия силы F, приложенной на свободном конце.

При расчете таких кривых стержней удобно определять положение сечения полярными координатами R и .

История механики показывает, что довольно долгое время кривые брусья рассчитывались по тем же формулам, что и прямые:
(14.1)



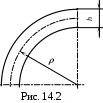Практика показывает, что в зависимости от кривизны бруса, первая из этих формула дает для кривых брусьев в некоторых случаях недопустимо большую ошибку (до 50%) в опасную сторону. Вторая и третья сохраняют достаточную точность. Поэтому в инженерной практике принято различать брусья малой и большой кривизны.

Брусом малой кривизны (рис.14.2) считают брус, у которого радиус кривизны 5h, где h – поперечный размер сечения бруса в плоскости кривизны. Такие брусья с достаточной точностью рассчитываются по формулам (14.1).

При 5hбудет брус большой кривизны; в этих случаях для определения напряжений требуются особые формулы.
14.2. Растяжение и сжатие кривого бруса
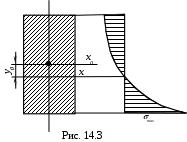
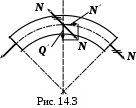В отличие от прямого бруса внешняя сила, приложенная нормально к какому – либо сечению кривого бруса (рис. 14.3), в других сечения вызывает изгибающие моменты и поперечные силы. Опыт показывает, что мало и гипотезой плоских сечений можно воспользоваться.

Тогда рассмотрим деформацию элемента бруса, характеризуемую только поворотом сечения на угол
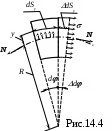
d вокруг центра кривизны (рис. 14.4).
Первоначальная длина произвольного волокна, отстоящего от центра тяжести на расстоянии y, равна



а удлинение этого волокна равно



Поэтому относительное удлинение



Если предположить, что волокна не оказывают давления друг на друга, то по закону Гука имеем



Эпюра нормальных напряжений показана на рис. 14.4. Равнодействующая соответствующих внутренних сил является продольная сила N , приложенная в центре тяжести сечения:

(14.2)

Следовательно, рассмотренная деформация кривого бруса соответствует случаю центрального растяжения (сжатия) прямого бруса.

Из формулы (14.2) получим подтверждение второй формулы из (14.1):

.


14.3. Чистый изгиб кривого бруса

Для определения напряжений при чистом изгибе плоского кривого бруса, так же как для прямого бруса, считаем справедливой гипотезу плоских сечений. Определяя деформации волокон бруса, пренебрегаем напряжением в радиальном направлении. Рассматриваем чистый изгиб кривого бруса у которого:

1) ось бруса – плоская кривая;

2) его поперечное сечение имеет ось симметрии, лежащую в плоскости кривизны бруса;

3) все нагрузки действуют в плоскости кривизны бруса, являющейся при сделанных ограничениях плоскостью его симметрии.

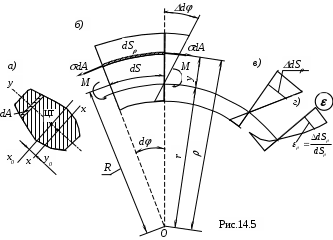
На рис. 14.5,а,б, показан элемент бруса длиной dS c симметричным поперечным сечением. Ось Ох направлена по нейтральной оси, вокруг которой поворачивается сечение.

Эпюра абсолютных удлинений волокон показана на рис. 14.5в, а эпюра относительных удлинений изображена на рис. 14.г.

Абсолютное удлинение по высоте сечения изменяется по закону прямой линии, а относительное – по закону кривой линии (гиперболы).




Объясняется это тем, что значение длины дуги
также меняется по высоте и поэтому для произвольного волокна, отстоящего от нейтрального слоя (х-х) на расстоянии у, имеем



Считая, что волокна друг на друга не давит, по закону Гука найдём

(14.3)

При чистом изгибе нормальная сила отсутствует, поэтому



Или с учетом (14.3) получим



Но так как множитель, стоящий перед интегралом, не может равняться нулю, то

(14.4)

Равенство (14.4) является условием для определения положения нейтрального слоя. Из равенства видно, что нейтральная ось в кривом брусе не проходит через центр тяжести, т.к. в последнем случае должен был бы равняться нулю статический момент как это было для прямого бруса.

Приравняем внешний момент моменту внутренних сил относительно нейтрального слоя через напряжения:

(14.5)

Интеграл, входящий в равенство (14.5), можно представить в виде



Второе слагаемое в полученном выражении согласно равенству (14.4) равно нулю, поэтому

(14.6)

где - статический момент площади поперечного сечения относительно нейтральной оси (у0 – расстояние от центра тяжести сечения до нейтральной оси).

Подстановка (14.6) в равенство (14.5) дает



Следовательно,

(14.7)

Подставляя полученное выражение в формулу (14.3) и учитывая. Что r+y=, т.е. равно расстоянию от центра кривизны до точки
, в которой определяется напряжение, окончательно получим

(14.8)
Формула (14.8) существенно отличается от формулы для прямого бруса.

Эпюра напряжений в сечении кривого бруса изменяется по гиперболическому закону(рис.14.6 ).

Наибольшие напряжения в сечениях, имеющих две оси симметрии, возникают в крайнем волокне, обращенном к центру кривизны. Знак напряжения определяют исходя из физического смысла.
Для того чтобы сравнить формулы для прямого и кривого брусьев, преобразуем (14.8). Из формулы (14.6) найдем



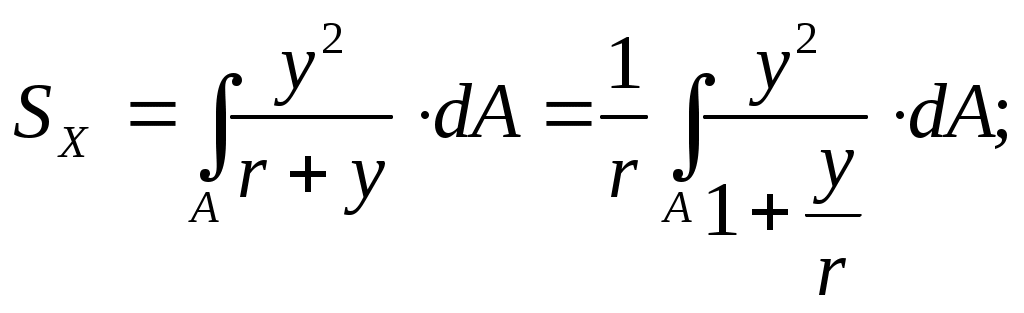
Обозначим



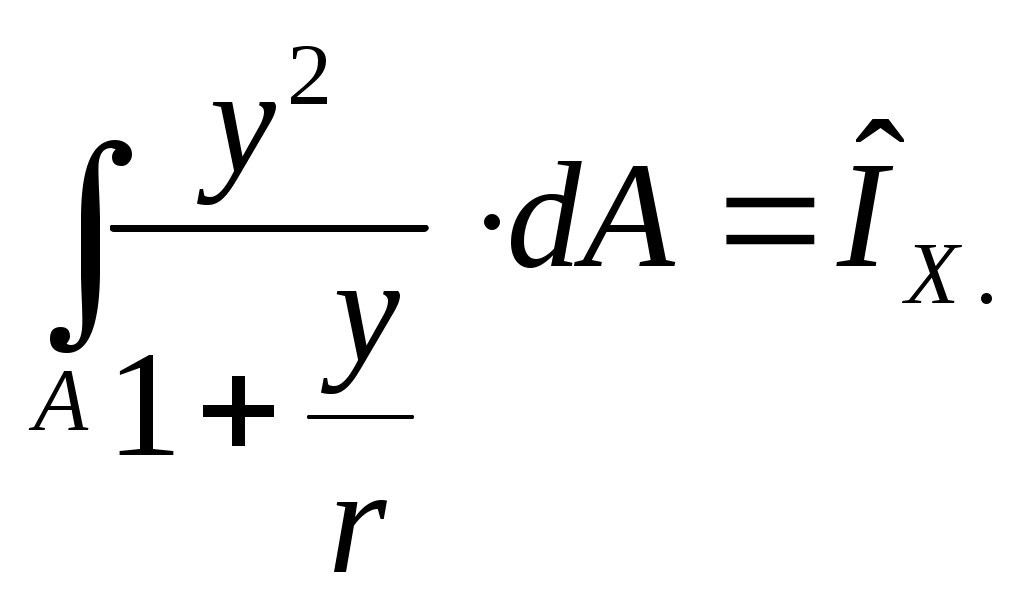
Этот интеграл назовем момент инерции для сечения кривого бруса.

Легко заметить, что при r момент инерции для сечения кривого бруса в пределе совпадает с обычным осевым моментом инерции.

Таким образом,

(14.9)

Подставляя это выражение в формулу (14.8) и учитывая, что r+y=, получим

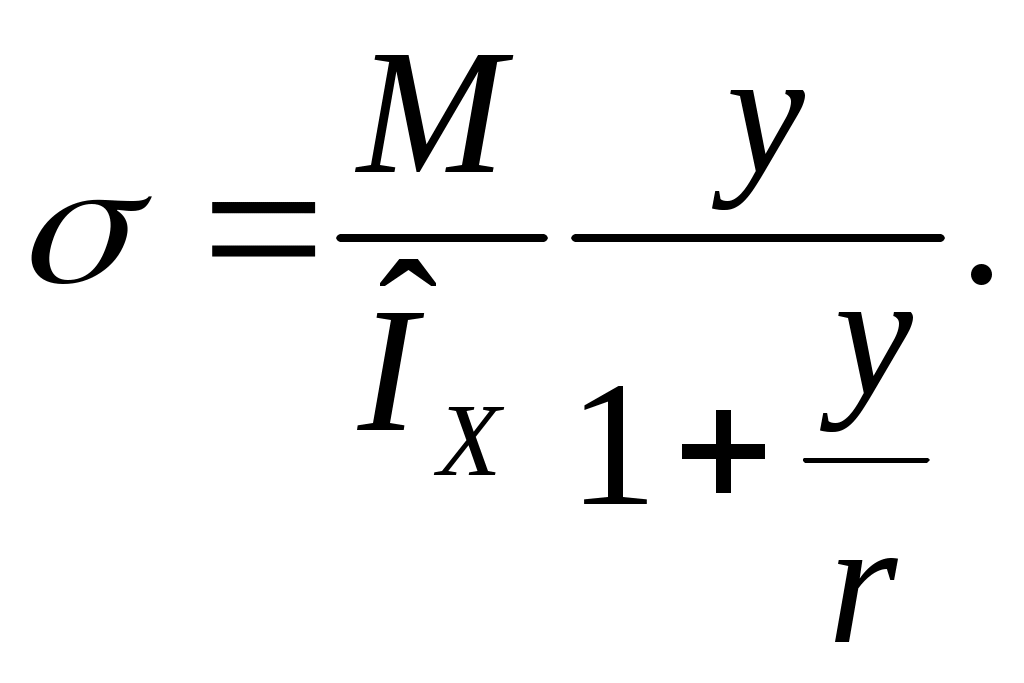(14.10)

Если r, то формула (14.10) в пределе совпадает с обычной формулой для прямого бруса.
14.4. Определение положения нейтральной оси в кривом брусе при чистом изгибе

Для определения напряжений по формуле (14.8) необходимо знать, как проходит нейтральная ось. Для этой цели надо определить радиус кривизны нейтрального слояr или расстояние от центра тяжести до нейтральной оси у0(рис 14.4). Зависимость между указанными величинами y0=R-rпозволяет, одну из них, легко определить другую.

При точном решении задачи необходимо исходить из условия (14.4). Для каждого типа поперечного сечения получится своё значение радиуса кривизны нейтрального слоя.

Преобразуем выражение (14.4). Учитывая, что = r+y; y= -r,

получим

Смотрите также файлы