Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Н 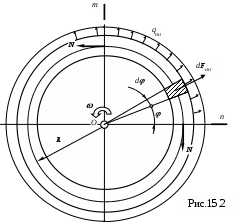ормальные напряжения в поперечных сечениях кольца

.

Отсюда определим допускаемую окружную скорость для различных материалов



1
5.2.3. Плоскопараллельное движение
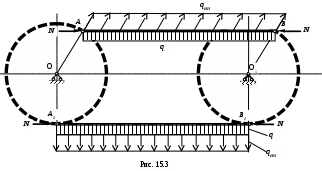
На рис. 15.3 изображена деталь АВ, встречающаяся в механизмах и называемая спарником. Его назначение – передача принудительного движения от одного колеса (вала) к другому. В спарнике возникают как продольные усилия (N), так и поперечные усилия от собственного веса и от сил инерции.

Точки спарника А и В равномерно двигаются по окружности радиуса r=OA=О₁В с угловой скоростью . Следовательно, при таком движении все точки спарника от А до В будут иметь одинаковое по величине и направлению нормальное ускорение а=а_n=²r, а возникающие силы инерции каждой элементарной массы на данный момент будут направлены вдоль радиуса точки А. Наиболее опасным оказывается крайнее нижнее положение, при котором силы инерции по направлению совпадают с силами веса.

Предполагая, что сечение спарника по длине постоянно и что вес его поэтому равномерно распределен и имеет интенсивность q(H/м) находим:



Изгибающий момент в опасном сечении спарника



Если ввести обозначения:



тогда

.

Так как спарник, помимо изгиба, подвергается также действию продольных сил, то имеем случай продольно- поперечного изгиба, для которого формула проверки прочности будет иметь вид:


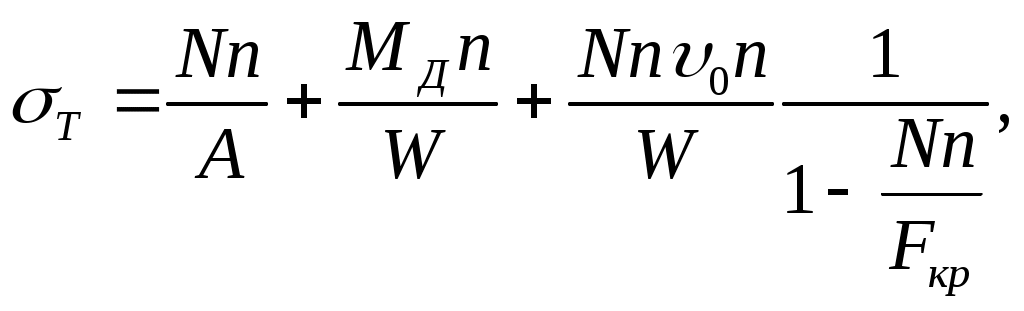
где n – число, показывающее, во сколько раз должны возрасти внешние силы, чтобы напряжение в опасной точке стало равным пределу текучести _Ти, которое сопоставляют с требуемым коэффициентом запаса прочности [n].

---

15.3. Удар

Ударные явления в механических системах весьма разнообразны, но их объединяют следующие общие черты:

1. 
   с кинематической стороны кратковременность акта соударения, в течение которого происходит резкое изменение скоростей точек системы;
   
2. 
   с динамической стороны – возникновение, а затем исчезновение весьма больших ударных сил.
   

Точная теория удара весьма сложная задача. Поэтому для расчетов на прочность и жесткость при ударе принимаем следующие допущения:

1. 
   напряжения в стержне при ударе не превышают предела пропорциональности; закон Гука соблюдается;
   
2. 
   удар является неупругим;
   
3. 
   деформации распространяются по стержню мгновенно (t=0);
   

Р
асчеты с учетом допущений базируются на законе сохранения энергии
T=U_Деф. (15.3)

Здесь Т – кинетическая энергия груза, которой он обладает в момент первого контакта.

U_Деф – потенциальная энергия деформация буфера к моменту его полного обжатия.

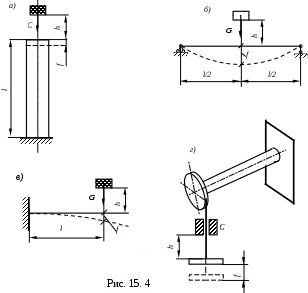
Система, подвергающаяся удару, может испытывать различные виды деформаций: сжатие (рис. 15.4,а), изгиб (рис. 15.4,б,в), кручение с изгибом (рис. 15.4,г) и др.
15.3.1 Поперечный удар.

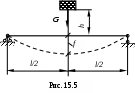
Рассмотрим невесомую балку постоянного сечения, шарнирно закрепленную на двух опорах ( рис. 15.5) и испытывающей посредине пролёта удар от падающего с высоты hгруза G=mg. Полагаем, что f = f_Ди чтопотенциальная энергия на момент полного обжатия П, полностью перешла в упругую энергию деформации балки U_Деф.
П= U_Деф (15.4)

или

, (15.5)
где

U_Деф=А= .
Приведём выражение (15.5) к уравнению

.

Решение



учтём, что

---

и получим динамический коэффициент

. (15.6)

Величину динамического коэффициента при падении груза на невесомую балку можно выразить через скорость падения груза в момент подлета к балке. Для этого необходимо вместо величины 2h подставить v²/g, что вытекает из формулы v²=2gh. Следовательно,

(15.7)

Когда высота падения равна нулю, динамический коэффициент равен двум. Такое загружение называется внезапным. Напряжения и прогибы в этом случае будут в два раза больше, чем при статическом нагружении при котором, как известно, предполагается постепенное нарастание величины нагрузки от нуля до конечного значения.

Если высота падения значительно превышает статический прогиб (h>>f_СТ), то единицей по сравнению со вторым членом, стоящим под корнем, можно пренебречь. Тогда

(15.8)

Не учитывается вес буфера, формулы (15.6), (15.7) и (15. используются во всех системах (рис.15. 4), подвергающихся удару, и испытывающих различные виды деформаций: сжатие (рис. 15.4,а), изгиб (рис. 15.4,б,в), кручение с изгибом (рис. 15. 4,г) и др.
Е сли груз падает на балку, обладающей значительной массой, которой нельзя пренебрегать, то решение сильно усложняется. Применяют приближенное решение: оно сводится к замене реальной балки системой с одной степенью свободы.

Распределенная по длине балки масса заменяется приведенной массой (Q₀ q), сосредоточенной в месте удара. Теорема об изменении кинетической энергии позволяет в этом случае определить f_Д , затем и k_Д :


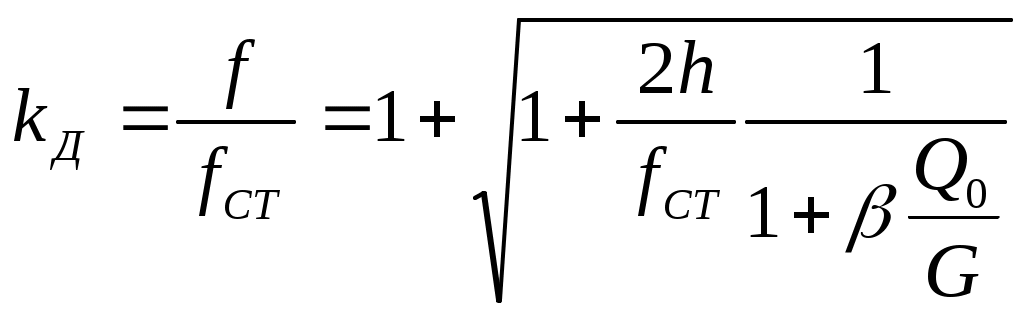(15.9)

где  - коэффициент приведения;

Q₀– вес балки ;

Q – вес приведенной массы;

G - весгруза.

Формула (15.9) используются во всех системах, подвергающихся удару (рис. 15.4), и испытывающих различные виды деформаций: сжатие (рис.15. 4,

---

а), изгиб (рис. 15.4,б,в), кручение с изгибом (рис. 15. 4,г) и др. В формуле (15.9) величина коэффициента приведения ( <1) изависит от способов крепления стержня и вида удара (продольный или поперечный удар).

Для определения величины применяют приближенный приём. Для этого определяют кинетическую энергию заданной системы и сравнивают её с кинетической энергией приведённой массы. Рассмотрим частный случай.

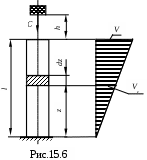
Продольный удар. Найдём величину для случая продольного удара по стержню постоянного сечения A, заделанного одним концом (рис.15.6). Пусть при ударе бесконечно малый элемент бруса с площадью поперечного сечения А и плотностью , имеющий массу

Аdz, получит скорость V_Z. Представим закон изменения скорости по высоте в виде



где V – скорость верхней точки бруса.

Кинетическая энергия бруса равна



Таким образом, для стержня заделанного одним концом, с весом Q₀=Alg, коэффициент приведения при продольном ударе =1/3.

При поперечном ударе коэффициент приведения =17/35.
15.3.2. Скручивающий удар.
На рисунке изображен простейший случай скручивающего удара. Вал диаметром d и длиной lс маховиком(шкив, абразивный камень) на правом конце, момент инерции которого J_m, вращающийся с угловой скоростью , внезапно заклинивается на левом конце. Так как маховик по инерции будет продолжать вращение, то вал начнет закручиваться, т.е. вся кинетическая энергия, которой обладает маховик, обратится в потенциальную энергию деформировавшегося вала.

Уравнение энергетического баланса имеет вид



или

(а)

где М_ДИН – величина, связанная с динамическим углом закручивания по закону Гука

.

Тогда из (а)

---

. (б)

Найдем напряжение и угол закручивания по обычным формулам кручения:

1) (в)

так как



следовательно, наибольшие напряжения зависят от модуля упругости и объёма вала ;

2) (г)
15.4. Колебание системы с одной степенью свободы

15.4.1. Виды колебаний системы с одной степенью свободы
Вообще упругая система или балка может давать колебания различного типа.

Все зависит от числа независимых параметров – т.е. от числа степеней свободы. Простейший случай: система с одной степенью свободы (рис. 15.7) система с двумя степенью свободы (рис. 15.8а,б).




Колебание системы с одной степенью свободы подразделяются на:

1 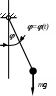) Свободные колебания.

Система выведена из состояния покоя и предоставлена

сама себе.



Уравнение без правой части.

2) Вынужденные колебания.

a) Силовое возбуждение (F(t)). б) Кинематическое возбуждение f(t).











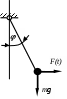
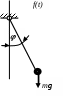
Уравнение справой частью. Силовое возбуждение от движения системы не зависит.

3)Параметрические колебания

П 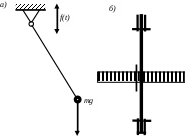араметрические колебания это такие колебания в процессе которых периодически меняются физические параметры системы, которые кинематически представлены на рисунке а), например, перемещение шестерни вдоль вала (рис. б)).
Получим уравнение без правой части

---