Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 411
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
. (3.14)
Второе слагаемое – удлинение от собственного веса: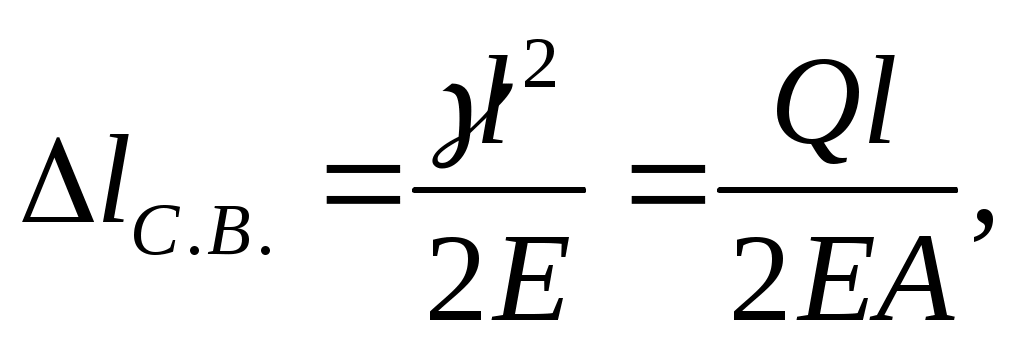
где Q=lA – вес стержня.
Подсчитаем напряжения по сечению I-I , расположенному на расстоянии zот свободного конца (см. рис. 3.8.) Выделим нижнюю часть с приложенными к ней внешними силами: грузом F и собственным весом Аz. Эти две силы уравновешиваются напряжениями (z), действующим по сечению I-I.
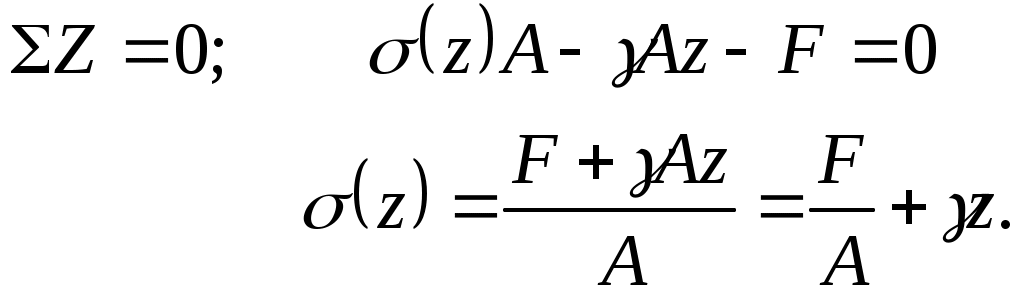(3.15)
Наиболее опасным будет верхнее сечение, где
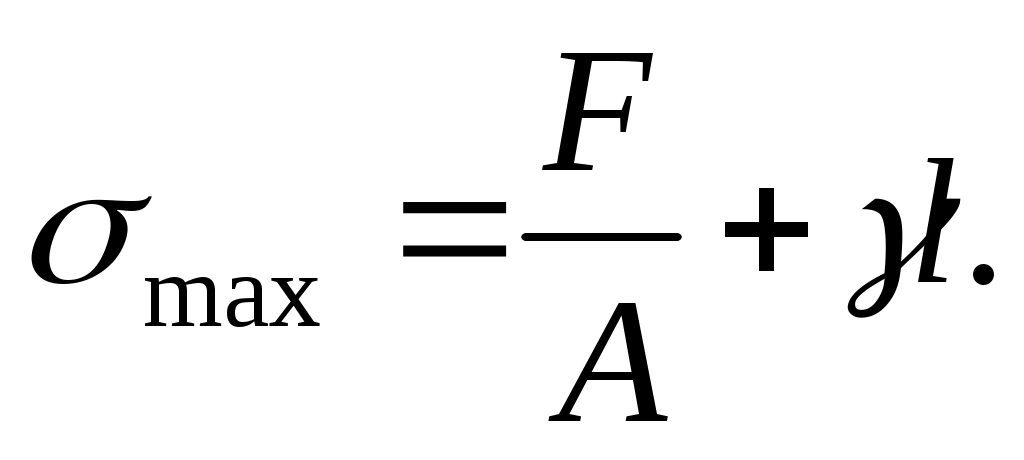(3.16)
3.4. Потенциальная энергия при растяжении и сжатии
Внешние силы, приложенные к телу совершают работу на вызванных ими перемещениях, при этом в теле накапливается энергия деформации – потенциальная энергия. За счёт накопленной энергии при снятии нагрузки восстанавливаются первоначальные размеры тела.
Рассмотрим призматический брус, растянутый силой F на величину l.
В процессе нагружения бруса сила медленно возрастала от 0 до F и совершала работу АЕ, которая в пределах упругих деформаций численно равна потенциальной энергии деформации:
АЕ = U.
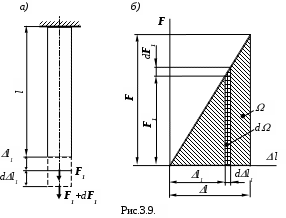
Пусть в процессе изменения растягивающей силы от 0 до F, когда она приняла некоторое значение F1 , удлинение будет l1 (рис. 3.9, а). Дадим силе F1 приращение dF1, тогда удлинение возрастет на величину dl1. Элементарная работа силыF1 на этом перемещении равна
dA = F1dl1.
Из рисунка 3.9,б видно, что величина F1dl1 равна узкой заштрихованной полоски диаграммы, поэтом
dA =d,
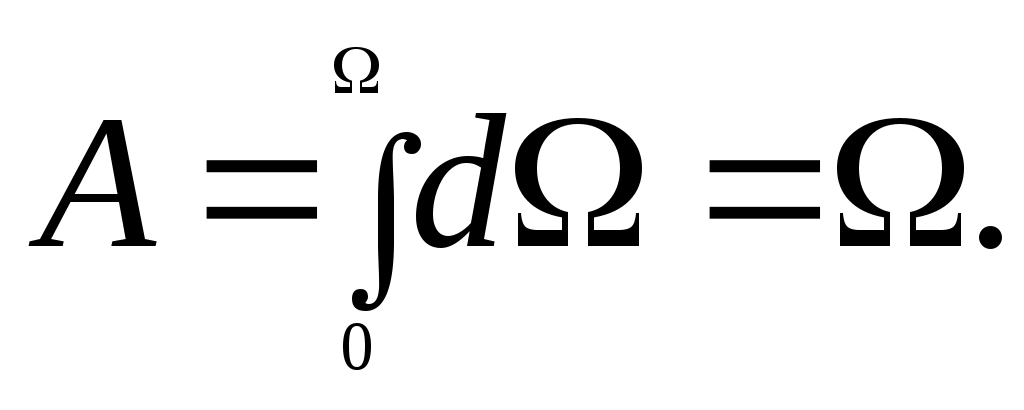
Таким образом, работа (а значит, и потенциальная энергия) равна площади диаграммы, которая в пределах упругих деформации имеет вид треугольника, поэтому
U = AЕ = 0,5Fl. (3.17)
Подставляя сюда вместо внешней силы F внутреннюю силу N и удлинение по формуле (3.9), получим
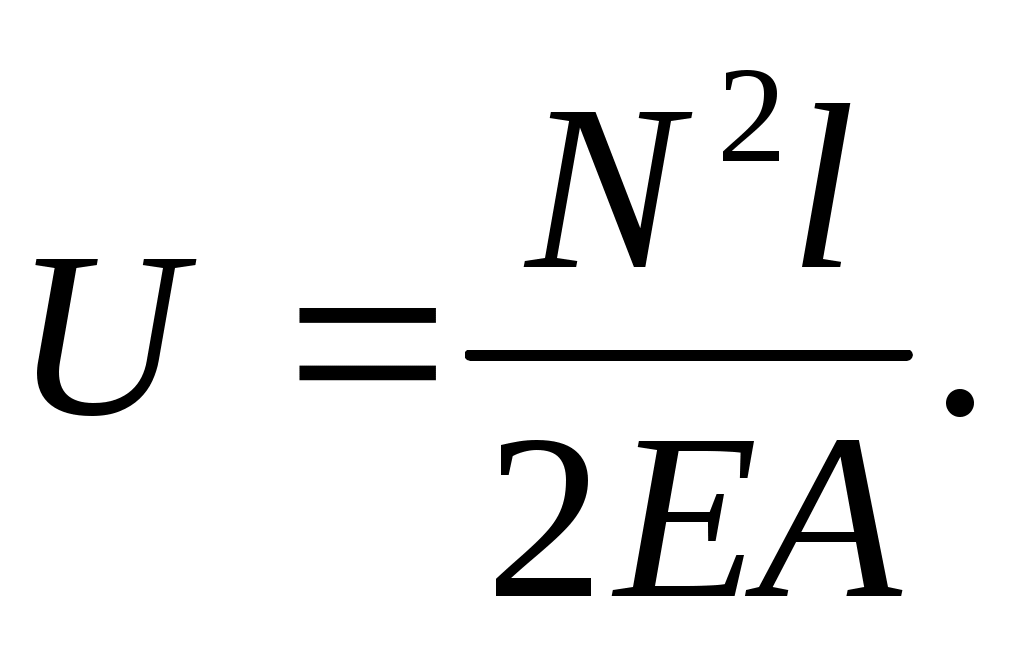(3.18)
Этой формулой можно пользоваться только для брусьев постоянного сечения на участке и при постоянной по длине участка бруса продольной силе N .
Если же поперечное сечение или продольная сила меняются по длине бруса постепенно, по какому – либо закону, то надо записать потенциальную энергию бесконечно малого отрезка бруса длиной dz, на протяжении которого поперечное сечение и внутренняя сила могут считаться постоянными,
после чего проинтегрировать это выражение по длине бруса:
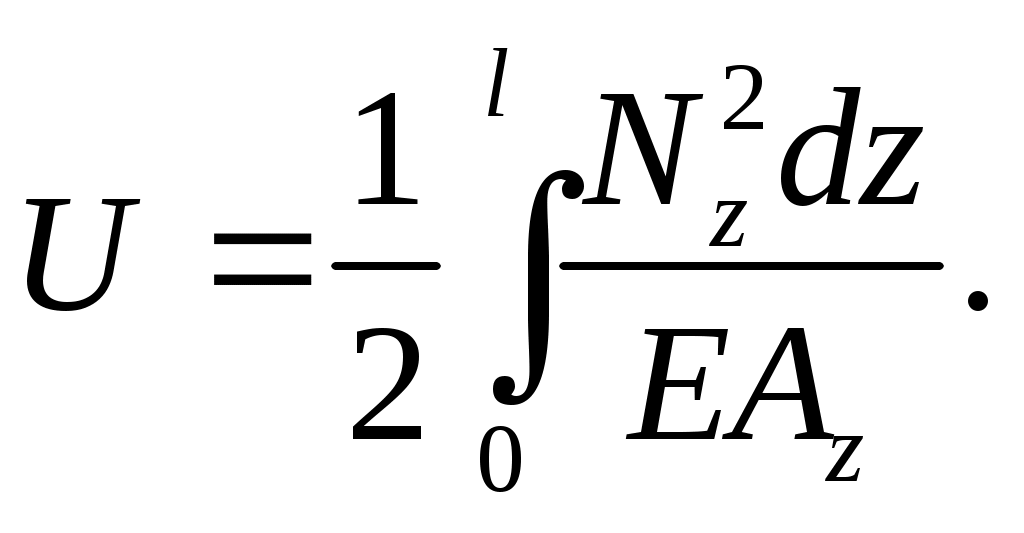(3.19)
3.5. Испытание материалов
3.5.1. Испытание материалов на растяжение
При проектировании и расчетах на прочность, жесткость и устойчивость элементов механизмов, машин и сооружений необходимо знать свойства материалов, из которых они будут изготовлены. Механические свойства материалов определяются при испытании их под нагрузкой.
При статической нагрузке основным видом испытаний является испытание на растяжение. По механическим характеристикам, получаемым при растяжении, так же можно получить данные для расчётов на прочность при других видах деформации.
3.5.1.1. Диаграмма растяжения.
3.5.1.2. Механические характеристики материалов
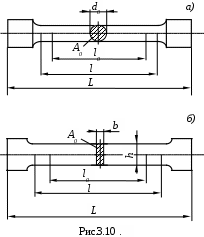
Для испытания на растяжение изготовляют специальные образцы из испытуемого материала и применяют соответствующие испытательные машины. Чаще применяют цилиндрические (рис 3.10, а); из листового металла изготовляют плоские образцы (рис 3.10, б).
Характер диаграммы растяжения зависит от свойств испытуемого материала. Типичный вид диаграммы растяжения для малоуглеродистой стали изображен на рис. 3.11.
Рассмотрим характерные участки и точки этой диаграммы и соответствующие им стадии деформирования образца.
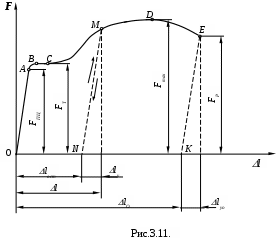
От начала нагружения до определенного значения растягивающей силы зависимость между удлинением образца и силой следует закону пропорциональности и на диаграмме выражается прямой линией ОА. На этой стадии растяжения справедлив закон Гука. Площадь поперечного сечения образца изменяется весьма незначительно и практически может быть принята равной начальному её значению А
0.
Обозначим силу, при которой закон пропорциональности прекращает своё действие, через FПЦ. Этому значению силы на диаграмме соответствует точка А. Напряжение, вызванное силой, называется пределом пропорциональности и вычисляется по формуле
пцFПЦ / А0. (3.20)
Таким образом, пределом пропорциональности называется наибольшее напряжение, до которого не наблюдается отклонение от закона пропорциональности.
За точкой А кривая растяжения отклоняется от прямолинейного участка и плавно поднимается до точки В, где наблюдается переход к так называемой площадке текучести ВС, имеющей направление, параллельное оси абсцисс. На этой стадии растяжения образцаего удлинение растёт при постоянном значении растягивающей силы, обозначаемой FТ. Такой процесс деформации, называемый текучестью материала, сопровождается остаточным (пластическим) удлинением, не исчезающим после разгрузки. При этом изменение поперечных размеров образца ещё незначительно.
Напряжение, при котором деформация образца происходит при постоянном усилии растяжения, называются пределом текучести.
Определяется предел текучести по формуле
ТFТ / А0. (3.21)
Начало пластической деформации соответствует наступлению некоторого
критического состояния металла, которое может быть обнаружено не только по остаточным деформациям, но и по ряду других признаков. При пластической деформации повышается температура образца; изменяется электропроводность и магнитные свойства; по направлению набольших касательных напряжений появляются линии сдвига.
После стадии текучести материал снова приобретает способность увеличивать сопротивление дальнейшей деформации и воспринимает возрастающее до некоторого предела усилие. Этому отвечает восходящий участок СD кривой растяжения, называемый участком упрочнения. Точка D соответствует наибольшему усилию, которое может воспринимать образец. Обозначим его через Fmax. Поперечные сечения испытуемой части образца до этого момента изменяются незначительно и равномерно по длине, удлинение распределяется также равномерно по длине испытуемой части образца.
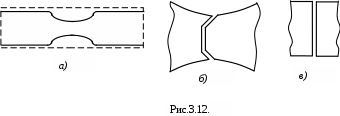
После достижения усилияFmax при дальнейшем растяжении образца деформация происходит, главным образом, на небольшой длине образца. Это ведет к образованию местного сужения в виде шейки (рис. 3.12, а) и к падению силы F, несмотря на то, что напряжение в сечении шейки непрерывно растёт.
Напряжение, отвечающее максимальной силе Fmax , называется временным сопротивлением или пределом прочности. Оно вычисляется по формуле
В Fmax / A0. (3.22)
Это напряжение условно, так как оно получено делением силы на площадь первоначального сечения А0, большую, чем действительная площадь сечения.
Обозначим через FР растягивающую силу в момент разрыва, получим
Р FР / A0. (3.23) Это напряжение при разрыве образца является совершенно условным и не может быть использовано в качестве характеристики механических свойств стали.
При разрыве образца появляется поперечная трещина в центре поперечного сечения посередине шейки, а остальное сечение скалывается под углом 450 к оси стержня, так что на одной части разорванного образца образуется выступ, а на другой – кратер (рис. 3.12 ,б). Такая форма разрушения образца из малоуглеродистой стали показывает, что разрушение связано со сдвигом по площадкам, наклонённым под углом 450 к оси стержня, где касательные напряжения будут наибольшими.
Чтобы иметь диаграмму, характеризующую механические свойства материала, перестраивают первичную диаграмму растяжения в диаграмму напряжений в координатах и (рис. 3.13.).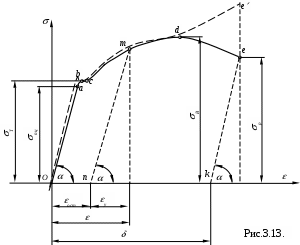
Эту диаграмму называют условной диаграммой растяжения, так как напряжения и относительные удлинения вычисляются соответственно по отношению к первоначальной площади сечения (А0) и первоначальной длине
образца (l0).
Основными характеристиками упругости и прочности материалов, используемых в практических расчетах, являются:
sПЦ – предел пропорциональности - превышение которого приводит к отклонению от закона Гука
;
sУ – предел упругости - напряжение, при котором остаточное удлинение достигает 0.05%;
sТ- предел текучести - напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют 0,2% (sТ =s0,2)
sПЧ(sВ) – предел прочности (временное сопротивление).
На диаграмме (рис. 3.13.) истинным напряжениям соответствует пунктирная кривая Ое. Так как истинная площадь поперечного сечения меньше первоначальной, то диаграмма истинных напряжений идёт выше диаграммы условных напряжений, особенно после образования шейки, когда происходит резкое уменьшение поперечного сечения образца.
Из диаграммы () видно, что
tqE, (3.24)
т.е. модуль продольной упругости при растяжении равен тангенсу угла наклона прямолинейного участка диаграммы к оси абсцисс.
Второе слагаемое – удлинение от собственного веса:
где Q=lA – вес стержня.
Подсчитаем напряжения по сечению I-I , расположенному на расстоянии zот свободного конца (см. рис. 3.8.) Выделим нижнюю часть с приложенными к ней внешними силами: грузом F и собственным весом Аz. Эти две силы уравновешиваются напряжениями (z), действующим по сечению I-I.
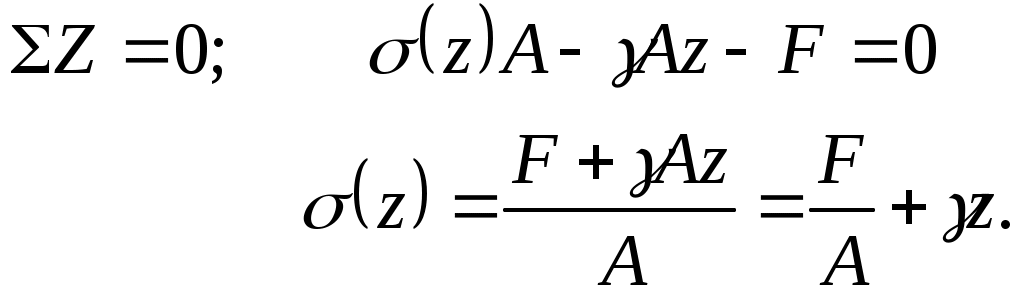(3.15)Наиболее опасным будет верхнее сечение, где
(3.16)3.4. Потенциальная энергия при растяжении и сжатии
Внешние силы, приложенные к телу совершают работу на вызванных ими перемещениях, при этом в теле накапливается энергия деформации – потенциальная энергия. За счёт накопленной энергии при снятии нагрузки восстанавливаются первоначальные размеры тела.
Рассмотрим призматический брус, растянутый силой F на величину l.
В процессе нагружения бруса сила медленно возрастала от 0 до F и совершала работу АЕ, которая в пределах упругих деформаций численно равна потенциальной энергии деформации:
АЕ = U.
Пусть в процессе изменения растягивающей силы от 0 до F, когда она приняла некоторое значение F1 , удлинение будет l1 (рис. 3.9, а). Дадим силе F1 приращение dF1, тогда удлинение возрастет на величину dl1. Элементарная работа силыF1 на этом перемещении равна
dA = F1dl1.
Из рисунка 3.9,б видно, что величина F1dl1 равна узкой заштрихованной полоски диаграммы, поэтом
dA =d,
Таким образом, работа (а значит, и потенциальная энергия) равна площади диаграммы, которая в пределах упругих деформации имеет вид треугольника, поэтому
U = AЕ = 0,5Fl. (3.17)
Подставляя сюда вместо внешней силы F внутреннюю силу N и удлинение по формуле (3.9), получим
(3.18)Этой формулой можно пользоваться только для брусьев постоянного сечения на участке и при постоянной по длине участка бруса продольной силе N .
Если же поперечное сечение или продольная сила меняются по длине бруса постепенно, по какому – либо закону, то надо записать потенциальную энергию бесконечно малого отрезка бруса длиной dz, на протяжении которого поперечное сечение и внутренняя сила могут считаться постоянными,
после чего проинтегрировать это выражение по длине бруса:
(3.19)3.5. Испытание материалов
3.5.1. Испытание материалов на растяжение
При проектировании и расчетах на прочность, жесткость и устойчивость элементов механизмов, машин и сооружений необходимо знать свойства материалов, из которых они будут изготовлены. Механические свойства материалов определяются при испытании их под нагрузкой.
При статической нагрузке основным видом испытаний является испытание на растяжение. По механическим характеристикам, получаемым при растяжении, так же можно получить данные для расчётов на прочность при других видах деформации.
3.5.1.1. Диаграмма растяжения.
3.5.1.2. Механические характеристики материалов
Для испытания на растяжение изготовляют специальные образцы из испытуемого материала и применяют соответствующие испытательные машины. Чаще применяют цилиндрические (рис 3.10, а); из листового металла изготовляют плоские образцы (рис 3.10, б).
Характер диаграммы растяжения зависит от свойств испытуемого материала. Типичный вид диаграммы растяжения для малоуглеродистой стали изображен на рис. 3.11.
Рассмотрим характерные участки и точки этой диаграммы и соответствующие им стадии деформирования образца.
От начала нагружения до определенного значения растягивающей силы зависимость между удлинением образца и силой следует закону пропорциональности и на диаграмме выражается прямой линией ОА. На этой стадии растяжения справедлив закон Гука. Площадь поперечного сечения образца изменяется весьма незначительно и практически может быть принята равной начальному её значению А
0.
Обозначим силу, при которой закон пропорциональности прекращает своё действие, через FПЦ. Этому значению силы на диаграмме соответствует точка А. Напряжение, вызванное силой, называется пределом пропорциональности и вычисляется по формуле
пцFПЦ / А0. (3.20)
Таким образом, пределом пропорциональности называется наибольшее напряжение, до которого не наблюдается отклонение от закона пропорциональности.
За точкой А кривая растяжения отклоняется от прямолинейного участка и плавно поднимается до точки В, где наблюдается переход к так называемой площадке текучести ВС, имеющей направление, параллельное оси абсцисс. На этой стадии растяжения образцаего удлинение растёт при постоянном значении растягивающей силы, обозначаемой FТ. Такой процесс деформации, называемый текучестью материала, сопровождается остаточным (пластическим) удлинением, не исчезающим после разгрузки. При этом изменение поперечных размеров образца ещё незначительно.
Напряжение, при котором деформация образца происходит при постоянном усилии растяжения, называются пределом текучести.
Определяется предел текучести по формуле
ТFТ / А0. (3.21)
Начало пластической деформации соответствует наступлению некоторого
критического состояния металла, которое может быть обнаружено не только по остаточным деформациям, но и по ряду других признаков. При пластической деформации повышается температура образца; изменяется электропроводность и магнитные свойства; по направлению набольших касательных напряжений появляются линии сдвига.
После стадии текучести материал снова приобретает способность увеличивать сопротивление дальнейшей деформации и воспринимает возрастающее до некоторого предела усилие. Этому отвечает восходящий участок СD кривой растяжения, называемый участком упрочнения. Точка D соответствует наибольшему усилию, которое может воспринимать образец. Обозначим его через Fmax. Поперечные сечения испытуемой части образца до этого момента изменяются незначительно и равномерно по длине, удлинение распределяется также равномерно по длине испытуемой части образца.
После достижения усилияFmax при дальнейшем растяжении образца деформация происходит, главным образом, на небольшой длине образца. Это ведет к образованию местного сужения в виде шейки (рис. 3.12, а) и к падению силы F, несмотря на то, что напряжение в сечении шейки непрерывно растёт. Напряжение, отвечающее максимальной силе Fmax , называется временным сопротивлением или пределом прочности. Оно вычисляется по формуле
В Fmax / A0. (3.22)
Это напряжение условно, так как оно получено делением силы на площадь первоначального сечения А0, большую, чем действительная площадь сечения.
Обозначим через FР растягивающую силу в момент разрыва, получим
Р FР / A0. (3.23) Это напряжение при разрыве образца является совершенно условным и не может быть использовано в качестве характеристики механических свойств стали.
При разрыве образца появляется поперечная трещина в центре поперечного сечения посередине шейки, а остальное сечение скалывается под углом 450 к оси стержня, так что на одной части разорванного образца образуется выступ, а на другой – кратер (рис. 3.12 ,б). Такая форма разрушения образца из малоуглеродистой стали показывает, что разрушение связано со сдвигом по площадкам, наклонённым под углом 450 к оси стержня, где касательные напряжения будут наибольшими.
Чтобы иметь диаграмму, характеризующую механические свойства материала, перестраивают первичную диаграмму растяжения в диаграмму напряжений в координатах и (рис. 3.13.).
Эту диаграмму называют условной диаграммой растяжения, так как напряжения и относительные удлинения вычисляются соответственно по отношению к первоначальной площади сечения (А0) и первоначальной длине
образца (l0).
Основными характеристиками упругости и прочности материалов, используемых в практических расчетах, являются:
sПЦ – предел пропорциональности - превышение которого приводит к отклонению от закона Гука
;
sУ – предел упругости - напряжение, при котором остаточное удлинение достигает 0.05%;
sТ- предел текучести - напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют 0,2% (sТ =s0,2)
sПЧ(sВ) – предел прочности (временное сопротивление).
На диаграмме (рис. 3.13.) истинным напряжениям соответствует пунктирная кривая Ое. Так как истинная площадь поперечного сечения меньше первоначальной, то диаграмма истинных напряжений идёт выше диаграммы условных напряжений, особенно после образования шейки, когда происходит резкое уменьшение поперечного сечения образца.
Из диаграммы () видно, что
tqE, (3.24)
т.е. модуль продольной упругости при растяжении равен тангенсу угла наклона прямолинейного участка диаграммы к оси абсцисс.