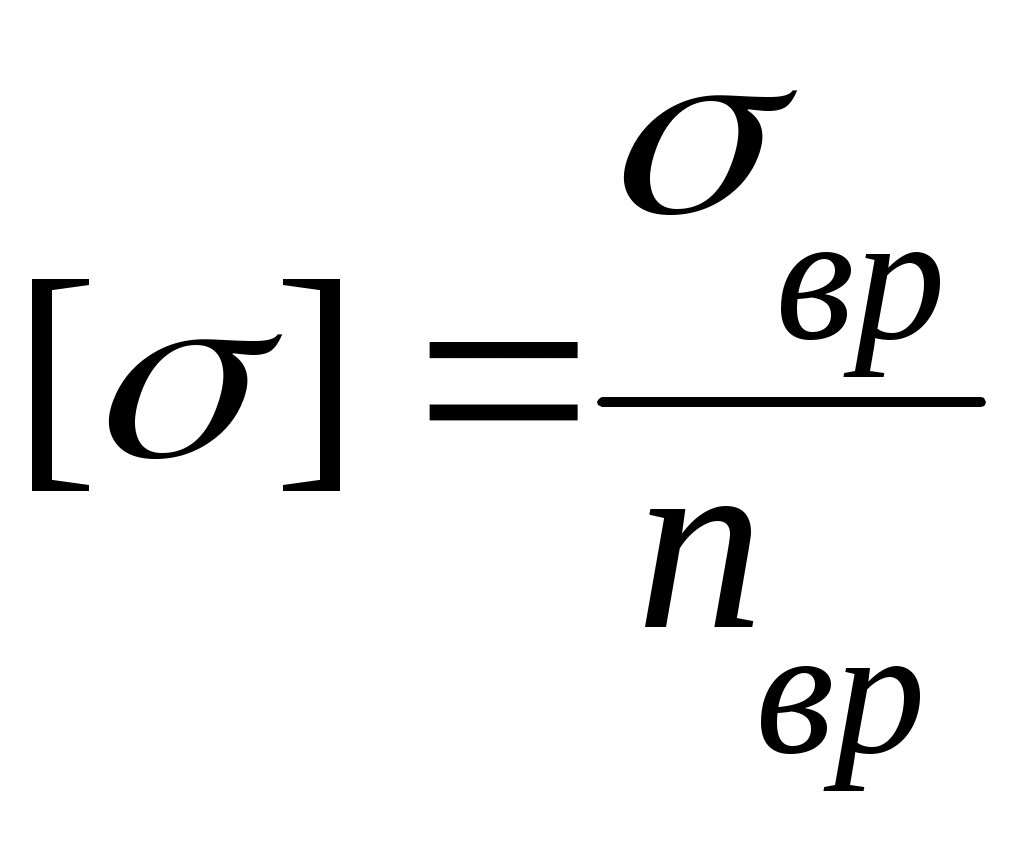Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

3.5.1.3. Характеристики пластичности материала
Кроме перечисленных выше характеристик прочности материала при испытании на растяжение определяют также относительное остаточное удлинение при разрыве _r являющееся важной характеристикой пластичности материла.

 (l₁l₀ l₀)100 %, (3.25)

где l₀ – первоначальная расчётная длина образца;

l₁ – расчётная длина образца после разрыва. Она измеряется после стыковки двух частей разорванного образца.

Для стали Ст.3  21%. У высокопрочных сталей эта величина снижается до 7 – 10 %.

Величина  зависит от соотношения между длиной образца и его поперечными размерами.

Второй характеристикой пластичности материала является относительное остаточное сужение при разрыве

₀₁₀100 %, (3.26)

где ₀– первоначальная площадь поперечного сечения;

₁ - площадь поперечного сечения в наиболее тонком месте шейки после разрыва.

Для стали Ст.3  (60 -70)%.

Величина - характеризует свойства пластичности более точно, чем , поскольку она в меньшей степени зависит формы образца.

3.5.1.4. Повышение предела пропорциональности

при повторном нагружении (наклёп)

Если испытуемый образец, не доводить до разрушения, разгрузить (точка М рис. 3.11.), то в процессе разгрузки зависимость между силой Fи удлинением l изобразится прямой MN. Опыт показывает, что эта прямая параллельна прямой ОА. При разгрузке удлинение полностью не исчезает. Оно уменьшается на величину упругой части удлинения (отрезок равный l_у). Отрезок ОN представляет собой остаточное удлинение (отрезок равный l_ост). Его называют также пластическим удлинением, а соответствующую ему деформацию – пластической деформацией. Таким образом,

l= l_у + l_ост. (3.27)

Соответственно

_у_ост. (3.28)

Если образец был нагружен в пределах участка ОА и затем разгружен, то удлинение будет чисто упругим

---

, и l_ост=0.

При повторном нагружении образца диаграмма принимает вид прямой NM и далее –по кривой MDE (рис. 3.11.) так, как будто промежуточной разгрузки и не было.

Следовательно, при повторных нагружениях образца, предварительно растянутого до возникновения в нём напряжений, больше предела текучести, предел пропорциональности повышается до того уровня, которого достигли напряжения при предшествующей нагрузке. Если между разгрузкой и повторным нагружением был перерыв, то предел пропорциональности повышается ещё больше.

Следует отметить, что диаграмма NMDE, получаемая при повторном нагружении, не имеет площадки текучести, поэтому для образца, претерпевшему разгрузку и повторное нагружение, определяется условный предел текучести (_0.2),который, очевидно, выше предела текучести при первичном нагружении.

Явление повышения предела пропорциональности и снижения пластичности материала при повторных нагружениях называется наклёпом.

Наклёп во многих случаях является нежелательным явлением, так как наклёпанный материал становится более хрупким. Поэтому наклёп часто снимают отжигом – нагревом до определённой температуры.

В целом ряде случаев наклёп полезен и его создают искусственно, например, в деталях подвергающихся воздействию переменных нагрузок, в арматуре, все цепи подвергаются наклёпу.

3.5.1.5. Сравнение диаграмм растяжения для различных материалов
Рассмотрим диаграммы растяжения некоторых других материалов. На рис. 3.14. для сравнения показаны диаграммы для сталей Ст.3, Ст.6, серого чугуна (СЧ), алюминиевых (Д16) и титановых (ВТ4) сплавов. Сталь Ст. 6 по сравнению со Ст. 3 обладает значительно более высокими характеристиками прочности. Площадка текучести у высокопрочных сталей , как правило, отсутствует или имеет очень малую протяжённость. У образцов из стали Ст. 6 при разрыве шейка не столь ярко выражена, как у стали Ст.3. Остаточная деформация при разрыве стали Ст.6 (13 -15 %) значительно меньше, чем у стали Ст. 3.


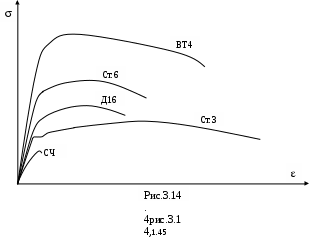
Диаграмма растяжения чугуна вообще не имеет прямого участка, она искривляется уже в самом начале. Чугун, строго говоря, вообще не подчиняется закону Гука. Для определения условного модуля упругости чугуна эту диаграмму спрямляют, заменяя кривую хордой. Диаграмма растяжения чугуна обрывается сразу после достижения предела прочности. Для различных сортов чугуна предел прочности при разрыве изменяется от 120 до 380 МПа. Разрыв чугуна происходит без образования шейки при малых остаточных деформациях (

---

0,5 %).
В зависимости от характеристик прочности и пластичности, а также характера разрушения все материалы делятся на две группы: пластичные и хрупкие.

Пластичные материалы (некоторые стали, медь, алюминиевые и титановые сплавы) имеют диаграммы растяжения, подобные диаграмме мягкой стали ( но без площадки текучести). И аналогичную форму разрушения образцов.

Хрупкие материалы (бетон, кирпич) имеют диаграммы растяжения, подобные диаграмме чугуна, и сходную форму разрушения (рис.3.14, рис.3.12 , в).
3.5.2. Испытание материалов на сжатие

3.5.2.1. Диаграмма сжатия. Особенности разрушения при сжатии
Для изучения ”поведения” материалов при сжатии строятся диаграммы сжатия.

Испытания металлов на сжатие производят на образцах в виде цилиндров, высота которых равна их диаметру (обычно d=h=6 -20 мм). Для других материалов применяют образцы в виде кубиков (стороны кубиков принимаются равными):

а =50 мм для дерева, 70 мм для цементаи 200 или 300 мм для бетона).
Р
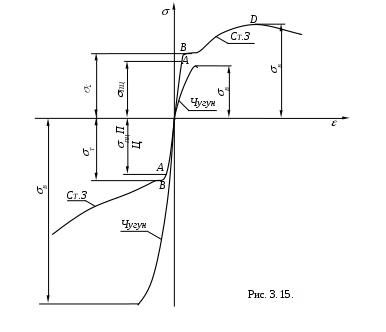
ассмотрим диаграммы сжатия стали и чугуна. Для наглядности изобразим их на одном рисунке с диаграммами растяжения этих материалов (рис. 3.15.).
В первой четверти диаграммы растяжения, а в третей – сжатия.

В начале загружения диаграмма, напряжений при сжатии малоуглеродистой пластичной стали Ст. 3, так же как и растяжения, представляет собой наклонную прямую, потом диаграмма закругляется и переходит в участок текучести.

Пределы пропорциональности и текучести для стали при сжатии приблизительно такие же, как и при растяжении. Углы наклона прямолинейных участков диаграммы при растяжении и при сжатии одинаковы, значит, равны и модули упругости.
С
тальной образец (рис. 3.16, а) при сжатии укорачивается, а поперечные размеры его увеличиваются, особенно в средней части.
По концам образца поперечные деформации затруднены наличием трения в местах соприкосновения с плоскостями испытательной машины, поэтому при сжатии цилиндр приобретает форму бочонка (рис. 3.16, б). При дальнейшем нагружении образец постепенно расплющивается (рис. 3.16, в), но разрушить его не удаётся, поэтому предел прочности установить нельзя.

---

Условно принимают при сжатии такой же предел прочности, как при растяжении.

Образы из других пластических металлов (медь, алюминий) при сжатии деформируются так же, как стальные образцы, и имеют аналогичную диаграмму напряжений при сжатии.

Диаграмма сжатия чугуна по форме похожа на диаграмму растяжения чугуна.

Эти диаграммы искривляются уже у самого начала и по достижении набольшей нагрузки резко обрываются (рис. 3.15.). Однако ординаты диаграммы напряжений при сжатии в несколько раз больше, чем при растяжении. Предел прочности на сжатие чугуна _в = 500 – 1500 МПа, т.е. в 4-5 раз больше, чем при растяжении. Таким образом, чугун работает на сжатие значительно лучше, чем на растяжение. При сжатии чугунного образца (рис. 3.17, а) продольные деформации его незначительны.

О
бразец несколько выпучивается в средней части, принимая слегка бочкообразную форму, после чего в нём появляются трещины под углом примерно 45⁰ к оси по площадкам с наибольшими касательными напряжениями (рис. 3.17, б).

В момент разрушения боковые части образца отделяются и он принимает вид двух усечённых конусов (рис. 3.17,в).

Большинство хрупких материалов (бетон, камень) разрушаются при сжатии так же, как и чугун, и имеет аналогичную диаграмму сжатия.


Предел прочности этих материалов на сжатие значительно больше, чем на растяжение (для бетона примерно в 20 раз). Все хрупкие материалы плохо

работают на растяжение.

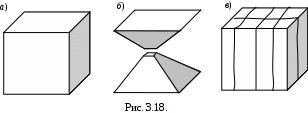
При раздавливании бетонных или цементных кубиков они принимают вид усеченных пирамид; на рисунках 3.18, а), б) показан бетонный кубик до и после разрушения. Если исключить влияние трения между сжимаемым бетонным кубиком и плоскостями машины, например, смазать эти плоскости парафином, то бетонный кубик разрушится по плоскостям, параллельным действующему усилию (рис. 3.18,в). Объяснить это можно в результате специального изучения этого вопроса.

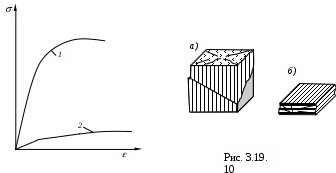
При испытании дерева на сжатие приходится учитывать, что дерево - материал анизотропный и по-разному работает вдоль и поперёк волокон. Диаграммы напряжений при сжатии дерева вдоль 1 и поперек 2 волокон показаны на рис. 3.19.

Многие породы дерева при сжатии вдоль волокон выдерживают значительные напряжения, например, предел прочности сосны достигает 40 – 80 МПа. В этом случае разрушение древесины происходит при сдвиге одной части кубика по другой (рис. 3.19,

---

а) . При сжатии дерева поперек волокон древесина не разрушается, а сильно прессуется (рис. 3.19, б).




3.5.2.2. Эффект Баушингера
Большой интерес представляет поведение образца, достигшего пластических деформаций при растяжении, который подвергается разгрузке и затем сжатию (или наоборот).

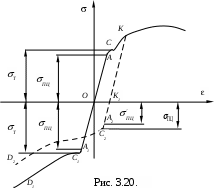
Рассмотрим диаграмму напряжений при растяжении и

сжатии стали (рис. 3.20.).




.

Если начиная от некоторой точки К диаграммы растяжения разгружать образец, диаграмма пойдёт по прямой КК₁и материал образца приобретёт наклёп. При последующем сжатии диаграмма пойдёт по кривой К₁ А₂ С₂ D₂ , которая располагается выше диаграммы сжатия образца, не подвергавшегося наклёпу ОА₁С₁D₁, и почти параллельно последней.

До наклёпа пределы пропорциональности и пределы текучести при растяжении и сжатии были примерно одинаковы. После наклёпа растяжением пределы пропорциональности и текучести при сжатии уменьшились, т.е. если после наклёпа подвергнуть материал деформации противоположного знака, то пределы пропорциональности текучести уменьшатся. Это явление называется эффектом Баушингера по имени учёного, впервые его описавшего.
3.6. Расчет по допускаемым напряжениям и перемещениям
В основе методики расчета по допускаемым напряжениям лежит сравнение расчетных напряжений с так называемыми допускаемым напряжением. Этот подход к оценке прочности конструкции предложен французским механиком и математиком Л.Навье в 1826г.

Допускаемые напряжения определяются как опасные, деленные на коэффициент запаса:

(3.29)

Для пластичных материалов опасное состояние характеризуется появлением значительных остаточных деформаций и опасным напряжением считается предел текучести. Тогда 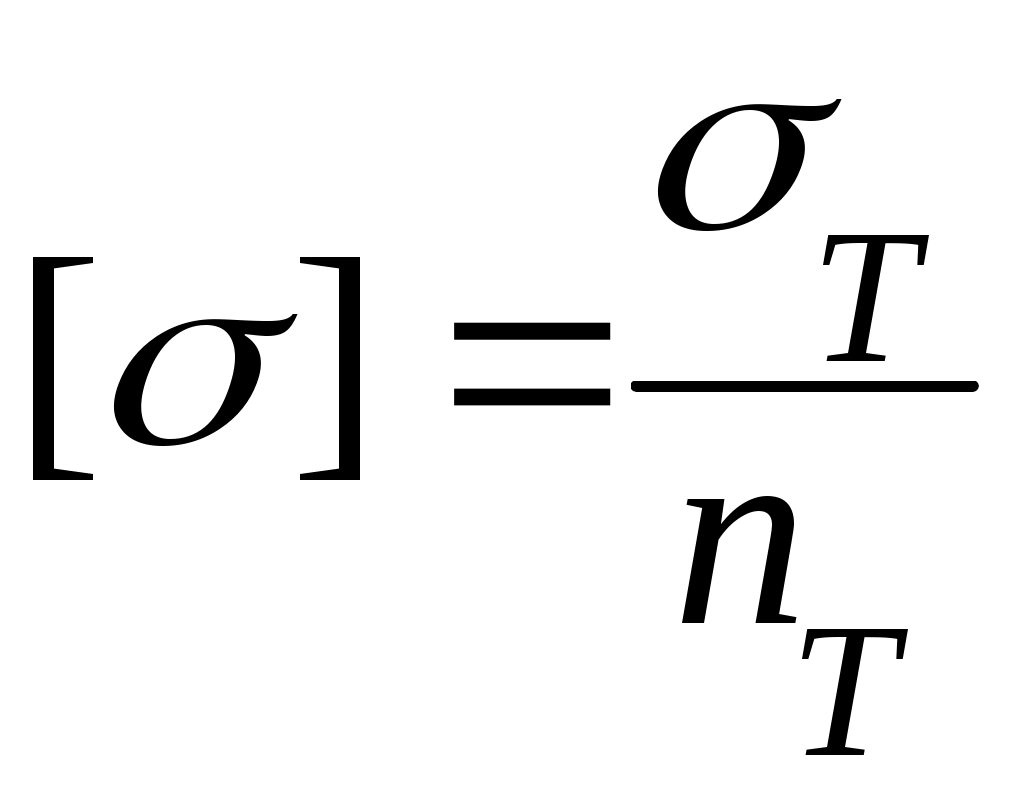(3.30)

Для деталей из хрупких материалов опасное состояние определяется появлением трещин. За опасное напряжение принимается предел прочности

---