Файл: Александры Анатольевны.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 135

Скачиваний: 5

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

B

КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ

КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ



В математике следует помнить

не формулы, а процессы мышления.

Ермаков В.П.

Основная цель: научить учащихся исследовать квадратные уравнения; ознакомить их с применениями теоремы Виета и теоремы, обратной ей.

Задачи, связанные с квадратными уравнениями, встречающиеся в школьной и конкурсной практике, чрезвычайно разнообразны.

Теория решения квадратного уравнения должна быть изложена достаточно полно по требованию программы. Однако для того, чтобы облегчить учащимся решение многих задач, я считаю необходимым дополнить теоретический материал. (Все изложенные ниже дополнительные сведения сообщаются учащимся в процессе изучения соответствующей темы, снабжаются множеством простых примеров. Доказывать все свойства не обязательно.)

СПРАВОЧНЫЙ МАТЕРИАЛ.

  • Уравнение вида Ax2 + Bx + C = 0, где x – неизвестное, A, B, C – действительные числа или выражения, зависящие только от параметров, причем A 0, называется квадратным уравнением относительно x.

  • Допустимыми считаются такие значения параметров, при которых A, B и C имеют смысл.

  • D = B2 – 4ac – дискриминант квадратного уравнения.

  • Если D 0, то уравнение корней не имеет.

  • Если D = 0, то уравнение имеет один корень кратности два: x = – .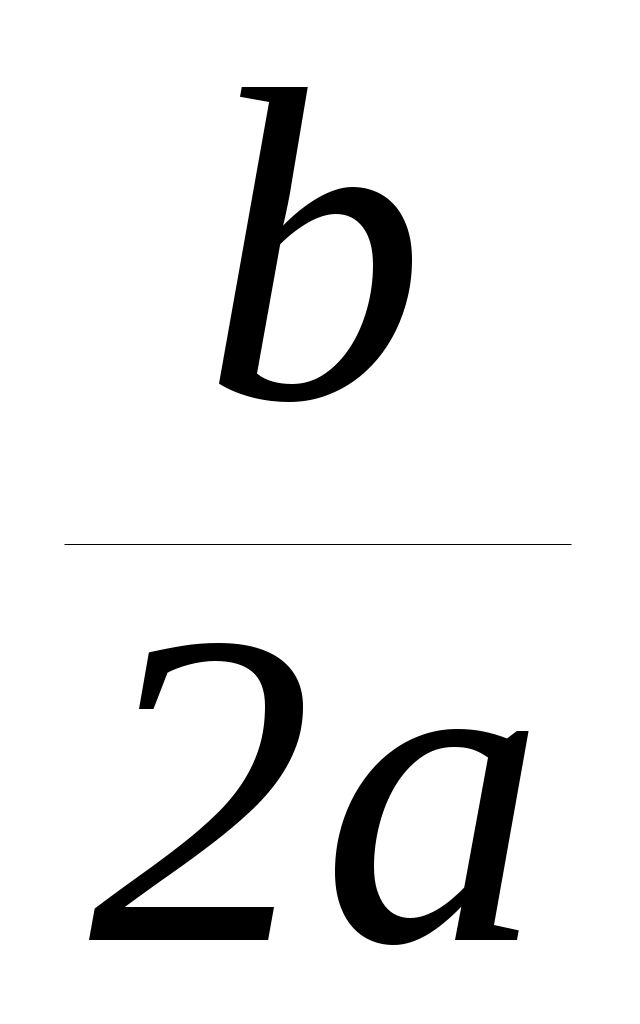

(Замечание: Часто про квадратные уравнения с дискриминантом, равным нулю, и имеющим, соответственно, один корень, говорят, что оно имеет два совпадающих корня (?). Это связано с разложением многочлена на множители. Правильнее, на мой взгляд, что в этом случае нужно говорить и понимать "один корень кратности два".)

  • Если D 0, то уравнение имеет два различных корня:

x1 = , x2 = .

  • Если b = 2k, то D1 = k2 – ac;

x1 = , x
2 = .

  • Теорема Виета. Если x1и x2 – корни квадратного уравнения ax2+bx+c = 0, то

x1 + x2 = – , x1 x2 = .

  • Для приведенного квадратного уравнения x2 + px+ q= 0 (при условии p2 4q)

x1 + x2 = – p; x1 x2 = q;

x2 – x1 = ; x1 2+ x2 2 = p2 – 2q.

  • Свойства корней квадратного уравнения:

  1. Если D 0, a 0, то уравнение имеет два действительных различных корня, знаки которых при C 0 одинаковы и противоположны знаку коэффициента b, а при C 0 разные, причем по абсолютной величине больше тот из корней, знак которого противоположен знаку b.

  2. Если D = 0, a 0, то уравнение имеет один корень кратности два, знак которого противоположен знаку b.

  3. Если D 0, a 0, то корней нет.

Аналогично устанавливаются свойства корней и для a 0.

Справедливы следующие утверждения:

  1. Если в квадратном уравнении поменять местами коэффициенты a и c, то получим уравнение, корни которого обратны корням данного.

  2. Если в квадратном уравнении поменять знак коэффициента b, то получим уравнение, корни которого противоположны корням данного.

  3. Если в квадратном уравнении коэффициенты a и c разных знаков, то оно имеет действительные корни.

  4. Если a 0, D = 0, то левая часть квадратного уравнения есть полный квадрат, и наоборот, если левая часть уравнения есть полный квадрат, то a 0, D = 0.

При изучении неполных квадратных уравнений в устную и письменную работу полезно включать такие задания:

  1. При каких значениях m ровно один из корней уравнения равен нулю:

а) 3x2
+ x + 2m – 3 = 0; б) x2 – 2x + m2 – 1 = 0;

в) 2x2 – mx + 2m2 – 3m = 0; г) x2 + (m + 3)x + m – 3 = 0.

  1. При каких значениях m корни уравнения равны по модулю, но противоположны по знаку:

а) x2 + (3m – 5)x – 2 = 0; б) 2x2 – (5m – 3)x + 1 = 0;

в) 3x2 + (m2 – 4m)x + m – 1 = 0; г) 4x2 + (5m – 1)x + 3m2 + m = 0.

  1. При каких значениях m корень уравнения кратности два равен нулю:

а) 3x2 – (m – 1)x – 1 – m2 = 0; б) x2 – (3m2 + 4m)x + 9m2 – 16 = 0;

в) 2x2 + (3m2 – mx) – m3 – 3m = 0; г) x2 + (16 – m4)x + m3 + 8 = 0.

  1. Решите уравнение:

а) x2+ a = 0; б) x2– 2x + 1 = 0; в) a2x2– 4 = 0; г) a(x2– 6x + 9) + 4 = 0.

К основным знаниям и умениям по этой теме относится умение решать полные квадратные уравнения.

Особенность решения этих уравнений заключается не только в том, что с изменением параметра у них меняются числовые коэффициенты, но и в том, что могут измениться важнейшие характеристики всего уравнения.

Начинать "общаться" с квадратными уравнениями следует с класса задач, где за счет параметра на переменную накладываются какие-либо искусственные ограничения. Для таких задач характерны следующие формулировки: при каком значении параметра уравнение имеет один корень, два корня, не имеет корней.

Обычно такие задачи не вызывают трудностей. Основное, что требуется от учащегося – это внимательность к формулировке.

  1. При каких значениях параметра c уравнение 5x2 – 4x + с = 0:

а) имеет действительные различные корни;

б) имеет один корень кратности два;

в) не имеет действительных корней?

Решение: D1 = 4 – 5c

а) Если D1 0, 4 – 5c 0, 5c 4, c 0,8 , то уравнение имеет два различных корня;


б) Если D = 0, 4 – 5c = 0, c = 0,8 , то уравнение имеет один корень кратности два;

в) Если D 0, 4 – 5c 0, 5c 4, c 0,8 , то уравнение не имеет корней.

Ответ: а) c 0,8;б) c = 0,8; в) c 0,8.

При работе с этим уравнением акцентируем внимание на следующих вопросах:

  • Какова степень уравнения?

  • Зависит ли степень уравнения от значения параметра с?

Далее усложняем задачу, предлагая уравнения, в которых коэффициент при второй степени неизвестной зависит от параметра.

  1. При каких значениях a уравнение ax2 + 2x + 1 = 0 имеет два различных корня?

Решение:

  1. Данное уравнение является квадратным относительно xпри a 0.

(Комментарий: первоначально учащиеся формулируют определение квадратного уравнения).

  1. Уравнение имеет различные корни, когда его D1 0.

D1 = 1 – a, 1 – a 0, a 1.

  1. При a = 0 получается уравнение 2x + 1 = 0, имеющее один корень.

Ответ: a ( 0) U (0; 1).

Формулируем правило:

  • Если коэффициент при x2многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль.

Опять с уравнением работаем очень подробно, обсуждая каждую деталь решения.

  1. Найти все значения параметра a, для которых квадратное уравнение

(a + 1)x2 + 2(a + 1)x + a – 2 = 0

а) имеет два различных корня;

б) не имеет корней;

в) имеет один корень.

Решение:

(Комментарий: Несколько раз прочитать формулировку, сравнить с предыдущим заданием, найти отличие в формулировках).

  1. Так как по условию уравнение квадратное, то a + 1 0, a –1.

(Вывод: Из решения следует исключить это число).

  1. D1= (a + 1)2 – (a + 1)(a – 2) = 12(a + 1).

а) Если D1 0, a + 1 0, a –1, то уравнение имеет два различных корня;

б) Если D1 0, a + 1 0, a –1, то уравнение не имеет корней;

в) Уравнение имеет один корень, если D1 = 0, a + 1= 0, a
= –1, но a –1 (из п.1), следовательно, решений нет.

Ответ: а) a –1;б)a –1; в)решений нет.

  1. При каких a уравнение ax2– x + 3 = 0 имеет единственное решение?

(Комментарий: Обсуждаем, какие из известных нам типов уравнений имеют один корень; каким может быть это уравнение в зависимости от a; определен ли в условии задачи тип уравнения).

Решение:

  1. Если a = 0, –x + 3 = 0, x = 3, то уравнение имеет один корень.

  2. Если a 0, то уравнение имеет один корень, когда D = 0.

D = 1 – 12a, 1 – 12a = 0, a = .

Ответ: a = 0, a = .

Задачи 36  39 являются ключевыми по этому вопросу.

В классе и для домашней работы можно предложить такие задачи:

  1. При каких значениях параметра b уравнение x2 + bx + 4 = 0:

а) имеет один из корней, равный 3;

б) имеет различные корни;

в) имеет один корень;

г) не имеет корней?

  1. При каких значениях параметра b корни уравнения 4x2 + (3b2 – 5 b + 2)x – 3 = 0 равны по модулю?

Ответ: ; 1.

  1. Найдите наибольшее целое значение k, при котором уравнение x2 + x – k = 0 не имеет корней.

  2. При каком значении a уравнение:

а) ax2 – (a + 1)x + 2a – 1 = 0; б) (a + 2)x2 + 2(a + 2)x + 2 = 0

имеет один корень?

Ответ: а) – ; 0 ; б) 0.

  1. При каких значениях a уравнение (a2 – 6a + 8)x2 + (a2 – 4)x + (10 – 3a – a2) = 0 имеет более двух корней?

Ответ: 2.

  1. Докажите, что при любом значении k уравнение 3y2 – ky – 2 = 0 имеет два корня.

  2. Докажите, что не существует такого значения m, при котором уравнение x2 – mx + m – 2 = 0 имело бы один корень.

Смотрите также файлы