ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 132
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
x =
Ответ: при a 2 корней нет;
при a = 2, 1 x 3;
при a 2, x1 =
Рассмотрим более сложный, но доступный восьмикласснику пример.
-
Сколько решений в зависимости от a имеет уравнение x + 2 = ax + 1?
Решение:
При x = 0 получаем 0 + 2 = a 0 + 1, т.е. x = 0 не является корнем уравнения ни при каких значениях параметра a.
Преобразуем уравнения с учетом, что x 0.
Построим графики функций y =
y
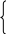 =
= 1 –
График функции y =
График функции y = –
При различных значениях параметра aграфиками функций y = a являются прямые, параллельные оси абсцисс.
При a1 иa 1 графики
имеют одну общую точку пересечения, уравнение имеет один корень;
При 1a ½ точек пересечения две, уравнение имеет два корня;
При ½ a 1 точек пересечения нет, уравнение корней не имеет;
При a = ½ один корень.
Ответ: при a1 один корень;
при 1a ½ два корня;
при a = ½ один корень;
при ½ a 1 корней нет;
при a 1 один корень.
 Пока мы не формулируем четкий алгоритм применения графического метода, только лишь устно составляем план решения задачи. Рассмотрение же таких задач с восьмиклассниками считаю необходимым, иначе в 10-11 классах при подготовке к экзаменам придется начинать все сначала, значит, теряется драгоценное время, ведь восстанавливать материал гораздо легче, чем изучать заново.
Пока мы не формулируем четкий алгоритм применения графического метода, только лишь устно составляем план решения задачи. Рассмотрение же таких задач с восьмиклассниками считаю необходимым, иначе в 10-11 классах при подготовке к экзаменам придется начинать все сначала, значит, теряется драгоценное время, ведь восстанавливать материал гораздо легче, чем изучать заново.ЛИНЕЙНЫЕ НЕРАВЕНСТВА С ПАРАМЕТРАМИ
Основная цель: сформировать умение решать элементарные линейные неравенства с параметрами.
В первую очередь расширим определение линейного неравенства.
Каждое из неравенств вида
AxB, AxB, AxB, AxB,
где Aи B – действительные числа или функции от параметров, а x– неизвестная величина, называется линейным неравенством с одним неизвестным (x).
Рассмотрим простейший пример:
-
Решить неравенство ax 1.
Невнимательный ученик быстро дает ответ x
 ax 1
ax 1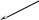

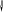
a 0a = 0a 0
ax 1 0x 1 ax 1



x
Учитель задает по заданию такие вопросы: "Каким будет решение, если вместо числа 1 записать ? вместо знака записать знак ?" и т.п. Ученики активно анализируют ответы своих одноклассников.
Затем учащиеся получают задание по вариантам составить блок-схемы к решению неравенств AxB, AxB, AxB, AxB. В тетрадях записываем словесное описание алгоритма.
Алгоритм решения линейных неравенств с параметрами
На примере неравенства Ax B,где x – неизвестное,
A, B – выражения, зависящие только от параметров)
-
Если A 0, то x  .
.
Решением неравенства являются все числа из промежутка (
-
а) Если A = 0, B 0
0 x B, x – любое число.
Решением неравенства является промежуток ( + ).
б) Если A = 0, B = 0
0 x 0, решений нет.
в) Если A = 0, B 0
0 x B, решений нет.
-
Если A 0, то x  .
.
Решением неравенства является промежуток (
Так как учащиеся еще не знакомы с методом интервалов, то выбор заданий по этой теме весьма ограничен. На этом этапе работы будет достаточно, если школьники усвоят решение простейших ключевых неравенств.
-
Решить неравенство (m – 1)x 5m.
Решение:
-
Если m – 1 0, m 1, то x 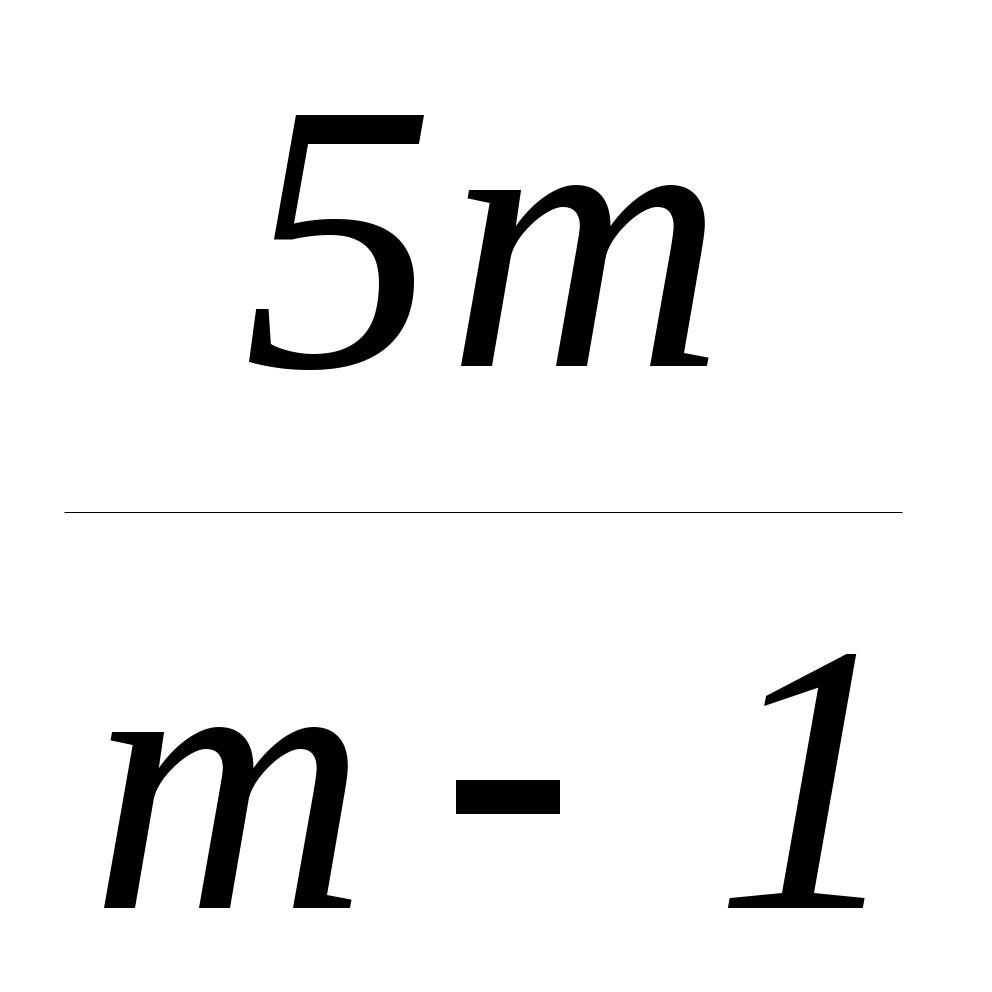 .
. -
Если m – 1 = 0, m = 1, получим
0 x 5, x – любое число.
-
Если m – 1 0, m 1, то x 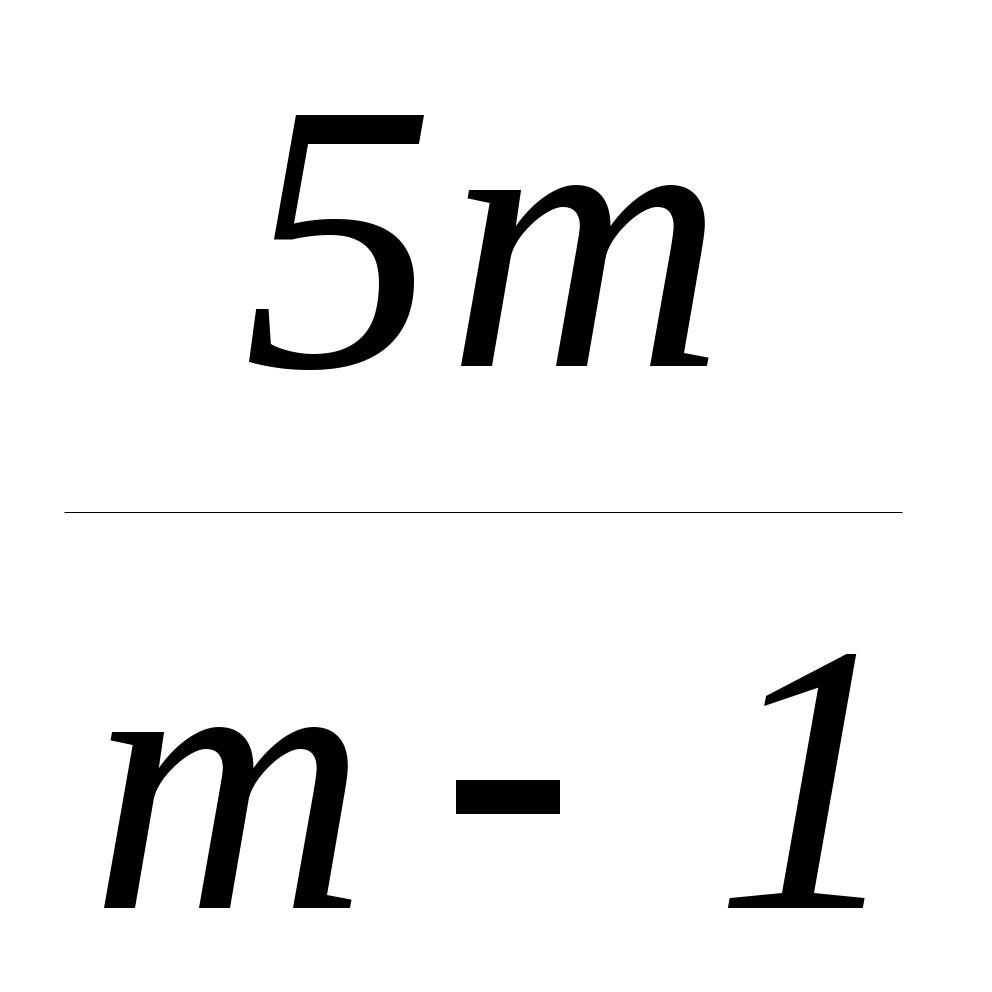 .
.
Ответ: при m 1, x
при m = 1, x – любое число;
при m 1, x
Несущественно, будут ли значения m и x записаны в форме неравенства или промежутка.
-
2ax + 5 a + 10x,
2ax – 10x a – 5,
(2a – 10)x a – 5,
2(a – 5)x a – 5.
-
Если 2(a – 5) 0, a – 5 0, a 5, то x 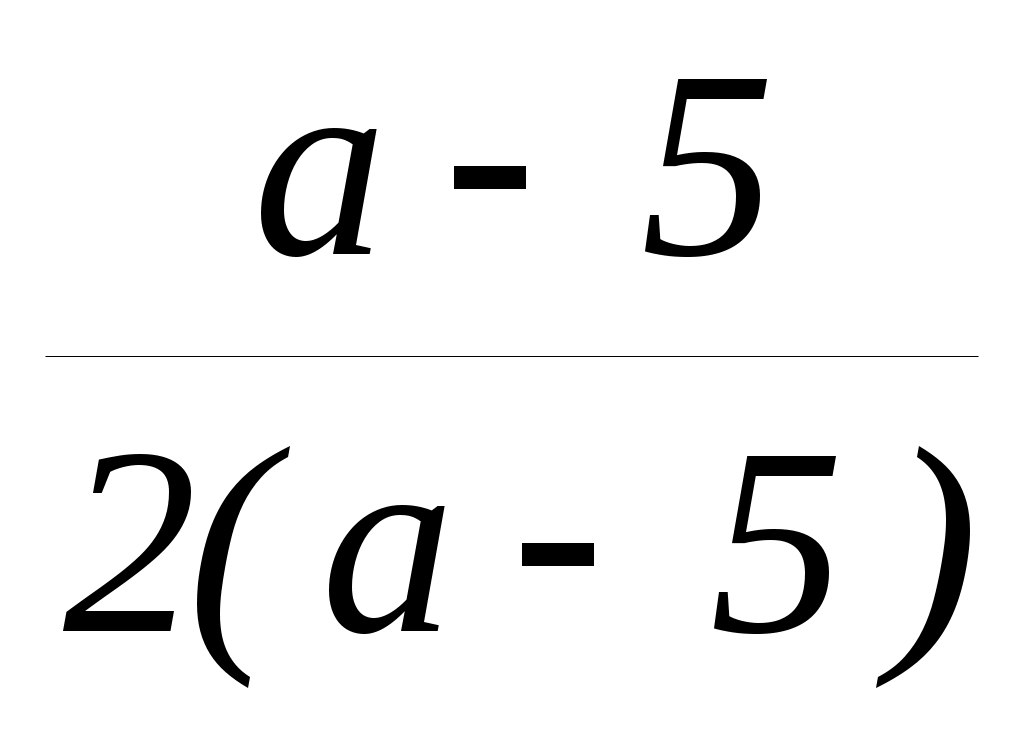 ; x
; x 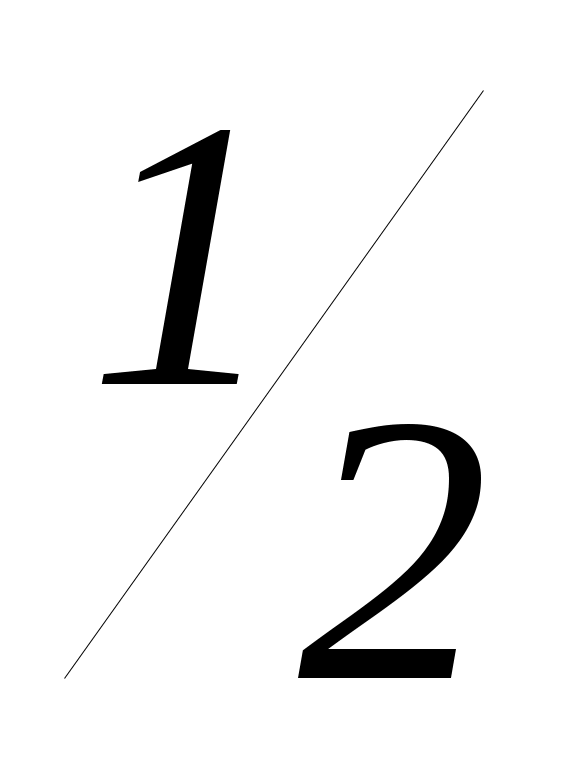 .
. -
Если 2(a – 5) = 0, a – 5 = 0, a = 5, то
0 x 0, решений нет.
-
Если 2(a – 5) 0, a – 5 0, a 5, то x 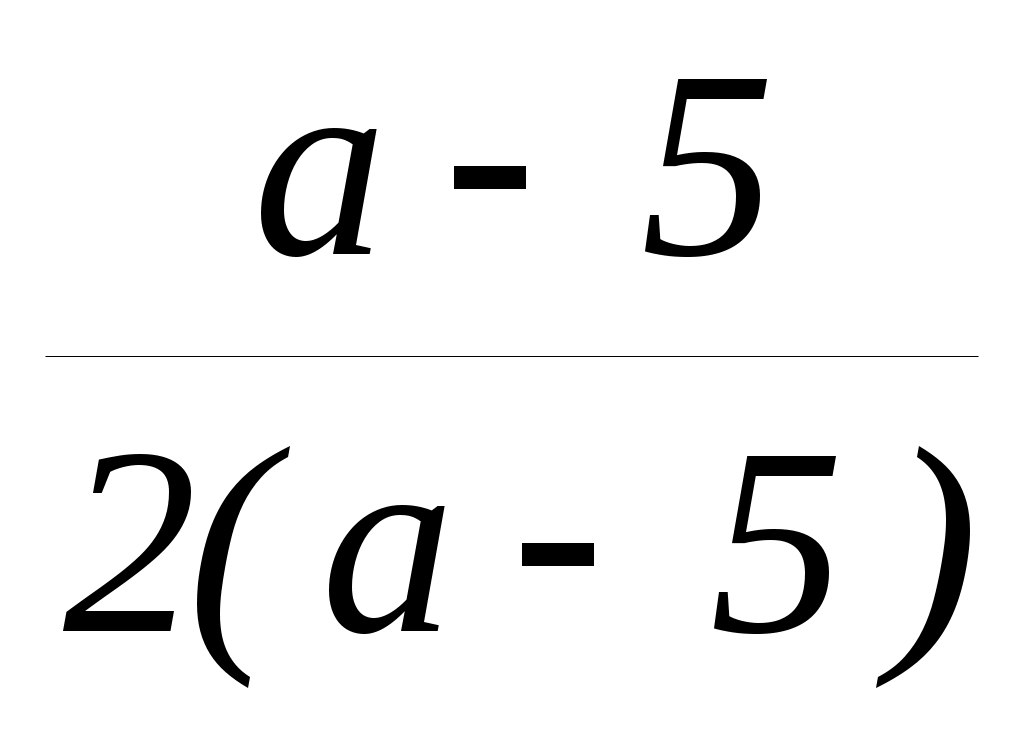 ; x
; x 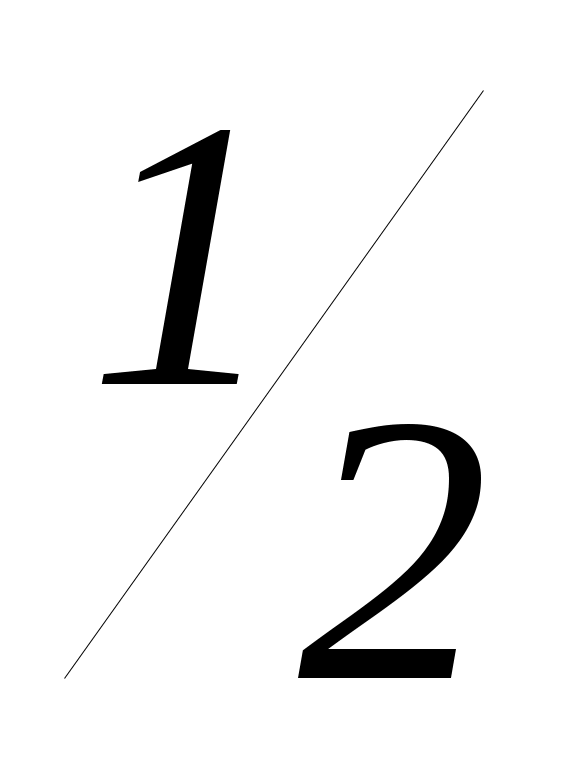 .
.
Ответ: при a 5, x
при a = 5, решений нет;
при a 5, x
-
mx – 6 2m – 3x,
mx + 3x 2m + 6,
(m + 3)x 2(m + 3).
-
Если m+3 0, m3, то x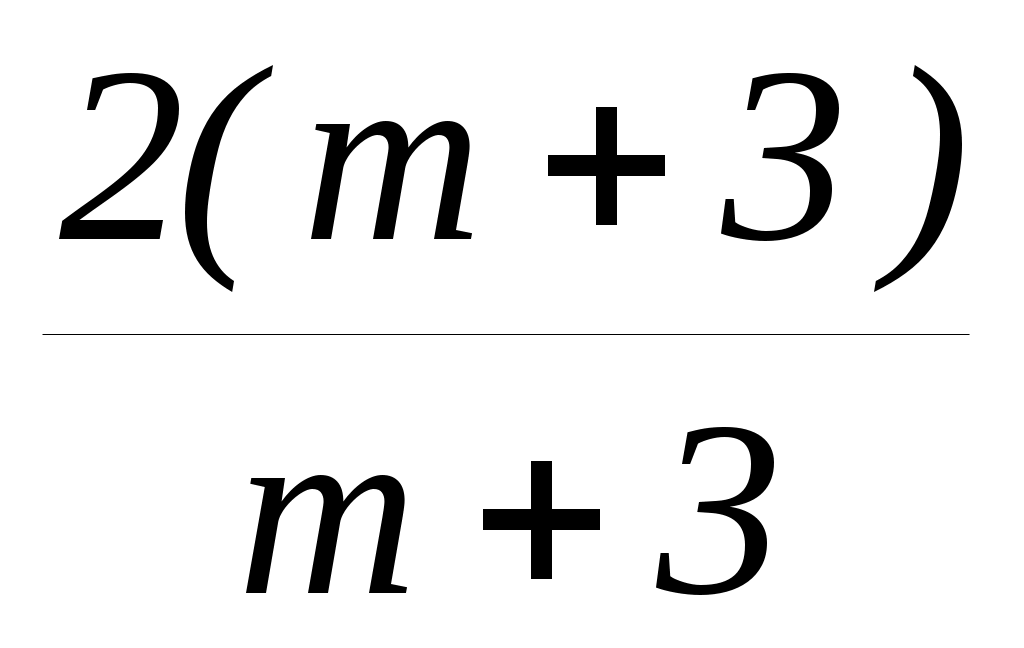 ; x 2.
; x 2. -
Если m+3 = 0, m = 3, то
0 x 0, x – любое число.
-
Если m+3 0, m3, то x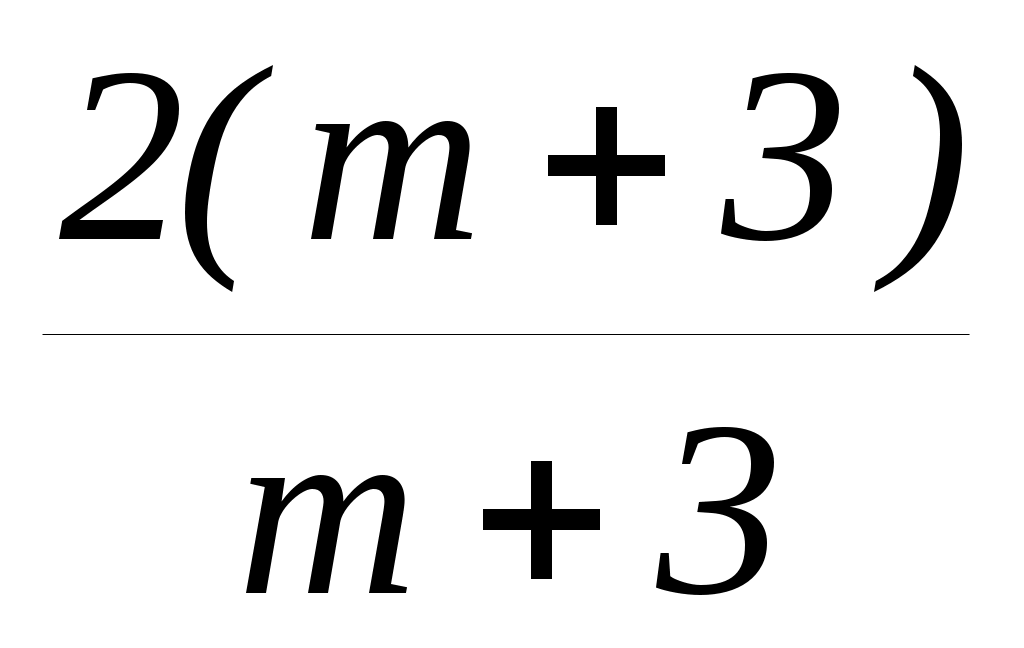 ; x 2.
; x 2.
Ответ: при m3, x 2;
при m = 3, x – любое число;
при m3, x 2.
Формальное решение неравенств 17, 18 приводит к распространенной ошибке, которая сводится к делению левой и правой частей неравенства на выражение, содержащее переменную, а это приводит к потере решений и коротким ответам.
Неправильно: x(m + 3) 2(m + 3), x 2.
-
5x – a ax – 3.
Ответ: при a 5, x
при a = 5, решений нет;
при a 5, x