Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 286
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, штриховка получается двойной: Δ < 0 при изменении ω от 0 до + ∞ (штриховка справа) и Δ > 0 при изменении ω от – ∞ до 0 (штриховка слева).
П
ример 5.17.
Определить область устойчивости в плоскости параметров Mи N для уравнения:
.
Полагая p = jω, образуем частотное уравнение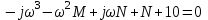
. Записываем его действительное и мнимое слагаемые в виде системы двух уравнений:
,
.
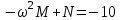Составляем определитель системы
и определители параметров:
, 
.
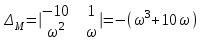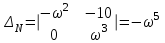Находим параметры:
, 
.
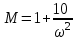При неограниченном возрастании частоты M стремится к еденице, N стремится к бесконечности. При стремлении ω к нулю M стремится к бесконечности, N к нулю. Вид кривой D - разбиения показан на рис. 5.27. Замена ω на - ω вида кривой не меняет.
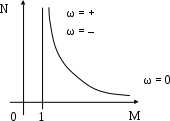
Рис. 5.27. Кривые D- разбиения по условиям примера 5.17
Для значений 0 ω + ∞ определитель Δ 0, штриховка наносится справа. Для – ∞ ω 0 определитель Δ 0, штриховка слева. Получается двойная штриховка в сторону области устойчивости, рис. 5.27.
1. Ким Д.П. Теория автоматического управления. Т1. Линейные системы. – М.: Физматлит, 2003. – 288 с.
2. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.
3. Востриков А.С., Французова Г.А. Теория автоматического регулирования. – М.: Высшая школа, 2004. – 365 с.
П
омимо требования быть устойчивой, к системе автоматического регулирования предъявляется требование по качеству регулирования.
Качество переходного процесса определяется совокупностью показателей, характеризующих приближение реального процесса к желаемому. О показателях судят, измеряя ряд величин в переходном процессе при единичном ступенчатом воздействии.
Показатели качества в переходном режиме подразделяют на прямые и косвенные. Прямые получают непосредственно по переходной функции. Косвенные рассчитывают.
6.1. Прямые показатели качества
Основной характеристикой качества САР является точность, которая оценивается ошибкой регулирования
.
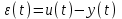Ошибка регулирования зависит от управляющего и возмущающего воздействий, а так же от характеристик САР. Обратимся к схеме на рис. 6.1. (W1(p), W2(p) передаточные функции регулятора и объекта регулирования соответственно).
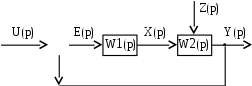
Рис. 6.1. Замкнутая система автоматического регулирования
Методом обратного движения построим операторное уравнение
,
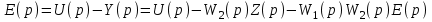или
.
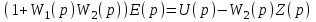Учтем формулу (4.12) передаточной функции по ошибке
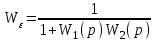
и получим:
.
Первое слагаемое делает вклад в ошибку регулирования от управляющего воздействия, второе – от возмущения. Передаточная функция
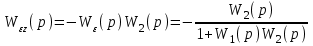(6.1)
есть передаточная функция по ошибке для возмущения.
Рассмотрим оценку точности в переходном процессе. Введем условие единичного ступенчатого воздействия,
u(t) = 1(t). Тогда переходной функцией будет h(t). Ошибка получает вид
.
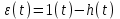Формула показывает, что ошибка отличается от переходной функции на постоянную величину. (При импульсном воздействии ошибка регулирования будет отличаться от таковой при единичном ступенчатом воздействии).
С течением времени h(t) стремится к установившемуся значению h(), а ошибка регулирования – к некоторому постоянному значению
.
Это значение ошибки называют статической ошибкой. Статическая ошибка есть рассогласование между установившемся значением регулируемой величины и ее заданным значением:
.
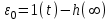Смысл статической ошибки заключается в следующем. Система исполняет регулирующую команду не до конца: когда достигается установившееся состояние, остается некоторое остаточное отклонение регулируемого параметра от заданного значения. Остаточное отклонение зависит от конструктивных особенностей САР и от величины управляющего воздействия.
Разность
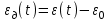
называют динамической ошибкой.
Систему автоматического регулирования с остаточной ошибкой в установившемся режиме называют статической системой.
Систему автоматического регулирования, которая исполняет регулирующую команду точно, называют астатической. В астатической системе регулируемый параметр по достижении равновесия принимает точно заданное значение.
Показатель качества «точность» оценивается не только статической и динамической ошибками, но также коэффициентами ошибок. Коэффициенты ошибок можно получить для управления и для возмущения.
Рассмотрим общий случай задающего воздействия u(t) в виде плавно изменяющейся функции времени. Как и при ступенчатом воздействии, в установившемся режиме будет иметь место ошибка ε(t). Ее можно представить в виде ряда
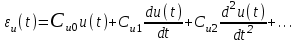(6.2)
где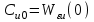
, 
, 
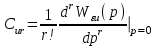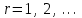
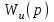
– передаточная функция относительно входа U(p) и выхода E(p). Коэффициенты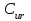
называются коэффициентами ошибки по задающему воздействию. (r= 0, 1, 2, …).
Установившуюся ошибку по возмущению так же можно представить в виде ряда
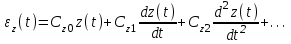(6.3)
, 
, 
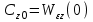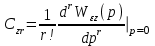Здесь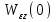
передаточная функция относительно входа z(p) и выхода Е(р). Коэффициенты 
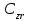называются коэффициентами ошибки по возмущению.
Первые три коэффициента ошибок имеют специальные названия: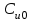
и 
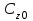коэффициенты позиционной ошибк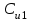и; 
и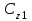 
коэффициенты скоростной ошибк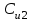и; 
и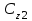 
коэффициенты ошибки по ускорению.
Быстродействие. Оценивается временем регулирования tp, рис. 6.2. Это промежуток времени, по истечении которого отклонение выходной величины от установившегося значения h() не превышает некоторой заранее заданной величины Δ. Последняя носит название «порог нечувствительности». Обычно назначают Δ в пределах (0,01 … 0,05) h().
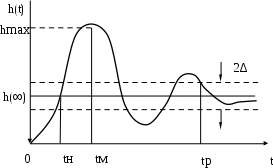
Рис. 6.2. Переходная функция
Наряду с tp для колебательных процессов используют две другие оценки быстродействия. Одна из них – время tн от начала процесса до первого пересечения кривой h (t) с прямой h = у(), рис. 6.2. Время tн называют временем нарастания переходного процесса. Другая – время tм достижения первого максимума, рис. 6.2.
Перерегулирование. Это максимальное отклонение регулируемой величины от установившегося значения
h(∞). Определяется в процентах:
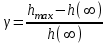(6.4)
hmax– максимальное значение переходной функции h(t) в момент времени tм, рис. 6.2.
Чем больше , тем более система склонна к колебаниям.
Число колебаний регулируемого параметра h(t) за время регулирования tp. Период колебаний определяется как 2/ω. Число колебаний рассчитывается как отношение времени регулирования к периоду колебаний:
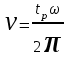. (6.5)
Числом колебаний характеризуют такое свойство системы, как колебательность. Колебательность системы больше, если больше число колебаний регулируемого параметра. И наоборот.
Специфические особенности системы регулирования могут потребовать дополнительные оценки качества. Например, точность воспроизведения входного сигнала, величина ошибки от возмущения и др.
П
ример 6.1.
Для системы, структурная схема которой изображена на рис. 6.1., найти установив-шуюся ошибку в предположении, что
, 
, 
, 
.
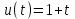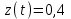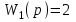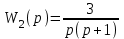Найдем передаточные функции ошибок по управлению,
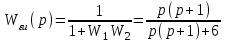
и по возмущению
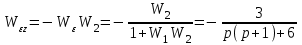
Вычислим ошибки.
.
.
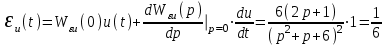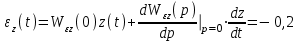Суммарная ошибка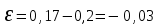
.
П
ример 6.2.
Дана система, в которой передаточная функция регулятора
,
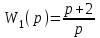передаточная функция объекта
.
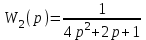Закон управления и закон возмущения имеют вид
П
ример 5.17.
Определить область устойчивости в плоскости параметров Mи N для уравнения:
.Полагая p = jω, образуем частотное уравнение
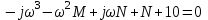. Записываем его действительное и мнимое слагаемые в виде системы двух уравнений: 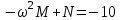, .Составляем определитель системы
и определители параметров:
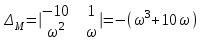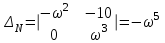, .Находим параметры:
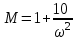, .При неограниченном возрастании частоты M стремится к еденице, N стремится к бесконечности. При стремлении ω к нулю M стремится к бесконечности, N к нулю. Вид кривой D - разбиения показан на рис. 5.27. Замена ω на - ω вида кривой не меняет.
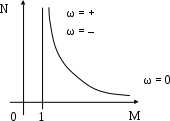
Рис. 5.27. Кривые D- разбиения по условиям примера 5.17
Для значений 0 ω + ∞ определитель Δ 0, штриховка наносится справа. Для – ∞ ω 0 определитель Δ 0, штриховка слева. Получается двойная штриховка в сторону области устойчивости, рис. 5.27.
Литература
1. Ким Д.П. Теория автоматического управления. Т1. Линейные системы. – М.: Физматлит, 2003. – 288 с.
2. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.
3. Востриков А.С., Французова Г.А. Теория автоматического регулирования. – М.: Высшая школа, 2004. – 365 с.
П
омимо требования быть устойчивой, к системе автоматического регулирования предъявляется требование по качеству регулирования. Качество переходного процесса определяется совокупностью показателей, характеризующих приближение реального процесса к желаемому. О показателях судят, измеряя ряд величин в переходном процессе при единичном ступенчатом воздействии.
Показатели качества в переходном режиме подразделяют на прямые и косвенные. Прямые получают непосредственно по переходной функции. Косвенные рассчитывают.
6.1. Прямые показатели качества
Основной характеристикой качества САР является точность, которая оценивается ошибкой регулирования
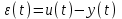.Ошибка регулирования зависит от управляющего и возмущающего воздействий, а так же от характеристик САР. Обратимся к схеме на рис. 6.1. (W1(p), W2(p) передаточные функции регулятора и объекта регулирования соответственно).
Рис. 6.1. Замкнутая система автоматического регулирования
Методом обратного движения построим операторное уравнение
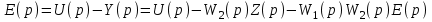,или
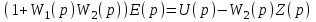.Учтем формулу (4.12) передаточной функции по ошибке
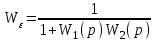
и получим:
.Первое слагаемое делает вклад в ошибку регулирования от управляющего воздействия, второе – от возмущения. Передаточная функция
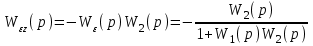(6.1)есть передаточная функция по ошибке для возмущения.
Рассмотрим оценку точности в переходном процессе. Введем условие единичного ступенчатого воздействия,
u(t) = 1(t). Тогда переходной функцией будет h(t). Ошибка получает вид
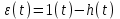.Формула показывает, что ошибка отличается от переходной функции на постоянную величину. (При импульсном воздействии ошибка регулирования будет отличаться от таковой при единичном ступенчатом воздействии).
С течением времени h(t) стремится к установившемуся значению h(), а ошибка регулирования – к некоторому постоянному значению
.Это значение ошибки называют статической ошибкой. Статическая ошибка есть рассогласование между установившемся значением регулируемой величины и ее заданным значением:
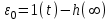.Смысл статической ошибки заключается в следующем. Система исполняет регулирующую команду не до конца: когда достигается установившееся состояние, остается некоторое остаточное отклонение регулируемого параметра от заданного значения. Остаточное отклонение зависит от конструктивных особенностей САР и от величины управляющего воздействия.
Разность
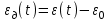
называют динамической ошибкой.
Систему автоматического регулирования с остаточной ошибкой в установившемся режиме называют статической системой.
Систему автоматического регулирования, которая исполняет регулирующую команду точно, называют астатической. В астатической системе регулируемый параметр по достижении равновесия принимает точно заданное значение.
Показатель качества «точность» оценивается не только статической и динамической ошибками, но также коэффициентами ошибок. Коэффициенты ошибок можно получить для управления и для возмущения.
Рассмотрим общий случай задающего воздействия u(t) в виде плавно изменяющейся функции времени. Как и при ступенчатом воздействии, в установившемся режиме будет иметь место ошибка ε(t). Ее можно представить в виде ряда
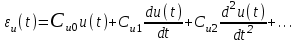(6.2)где
, ,
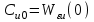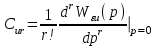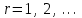
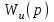
– передаточная функция относительно входа U(p) и выхода E(p). Коэффициенты
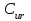называются коэффициентами ошибки по задающему воздействию. (r= 0, 1, 2, …).Установившуюся ошибку по возмущению так же можно представить в виде ряда
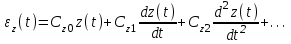(6.3)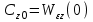 , , 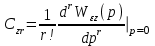Здесь
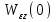передаточная функция относительно входа z(p) и выхода Е(р). Коэффициенты 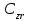называются коэффициентами ошибки по возмущению.Первые три коэффициента ошибок имеют специальные названия:
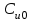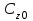и коэффициенты позиционной ошибк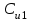и; и 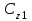коэффициенты скоростной ошибк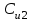и; и 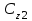коэффициенты ошибки по ускорению.Быстродействие. Оценивается временем регулирования tp, рис. 6.2. Это промежуток времени, по истечении которого отклонение выходной величины от установившегося значения h() не превышает некоторой заранее заданной величины Δ. Последняя носит название «порог нечувствительности». Обычно назначают Δ в пределах (0,01 … 0,05) h().
Рис. 6.2. Переходная функция
Наряду с tp для колебательных процессов используют две другие оценки быстродействия. Одна из них – время tн от начала процесса до первого пересечения кривой h (t) с прямой h = у(), рис. 6.2. Время tн называют временем нарастания переходного процесса. Другая – время tм достижения первого максимума, рис. 6.2.
Перерегулирование. Это максимальное отклонение регулируемой величины от установившегося значения
h(∞). Определяется в процентах:
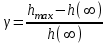(6.4)hmax– максимальное значение переходной функции h(t) в момент времени tм, рис. 6.2.
Чем больше , тем более система склонна к колебаниям.
Число колебаний регулируемого параметра h(t) за время регулирования tp. Период колебаний определяется как 2/ω. Число колебаний рассчитывается как отношение времени регулирования к периоду колебаний:
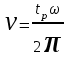. (6.5)Числом колебаний характеризуют такое свойство системы, как колебательность. Колебательность системы больше, если больше число колебаний регулируемого параметра. И наоборот.
Специфические особенности системы регулирования могут потребовать дополнительные оценки качества. Например, точность воспроизведения входного сигнала, величина ошибки от возмущения и др.
П
ример 6.1.
Для системы, структурная схема которой изображена на рис. 6.1., найти установив-шуюся ошибку в предположении, что
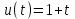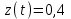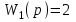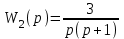, , , .Найдем передаточные функции ошибок по управлению,
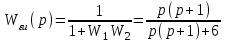
и по возмущению
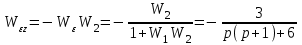
Вычислим ошибки.
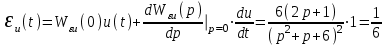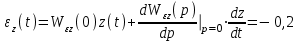. .Суммарная ошибка
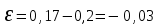.П
ример 6.2.
Дана система, в которой передаточная функция регулятора
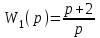,передаточная функция объекта
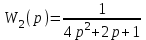.Закон управления и закон возмущения имеют вид