Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx

.

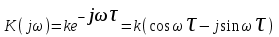Действительная частотная характеристика U(ω) = k cosω 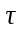, мнимая частотная характеристика V(ω) = – k sin ω .

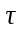Амплитудная частотная характеристика – постоянная величина:

.

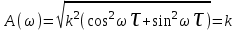Амплитуда не зависит от частоты, входной сигнал не изменяется.

Составляя 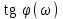, обнаруживаем, что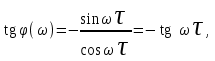



откуда фазовая частотная характеристика:

φ(ω) = – φ.

Для фиксированного времени запаздывания τзависимость от частоты линейная. Запаздывание по фазе нарастает с увеличением частоты.

Логарифмическая амплитудная частотная характеристика

L(ω) = 20 lg A(ω) = 20 lg k.

Переходная функция запаздывающего звена h(t) = k1(t-τ). На выходе звена получается скачок спустя  секунд после воздействия на входе, рис. 3.1.

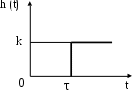
Рис. 3.1. Переходная функция запаздывающего звена

3.3. Инерционное звено
Другое название - апериодическое звено первого порядка. Описывается дифференциальным уравнением

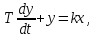(3.3)

где Т – постоянная времени звена, k – коэффициент усиления.

Операторное уравнение

(Tp + 1)Y(p) = kX(p).

Передаточная функция



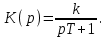
При p = 0 передаточная функция вырождается в коэффициент усиления. (p = 0 означает отсутствие изменения выходной величины, dy/dt = 0, что превращает инерционное звено в усилительное).

Комплексная частотная характеристика



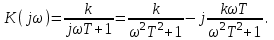
Действительная и мнимая частотные характеристики

---

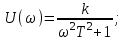
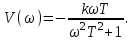
При ω = 0 амплитуда равна коэффициенту усиления, с увеличением ω стремится к нулю.

Амплитудная частотная характеристика:



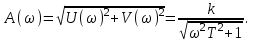
Фазовая частотная характеристика:



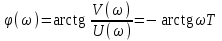
Она представляет собой кривую, асимптотически приближающуюся к величине φ(∞) = – π/2.

Логарифмическая амплитудная частотная характеристика:

.

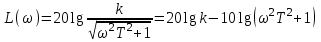Найдем асимптотические прямые логарифмической амплитудной частотной характеристики. В области низких частот, ω< 1, асимптотой будет 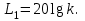В области высоких частот, ω> 1, асимптотой будет 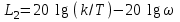. Прямая L₂ пересекает ось абсцисс при lg ω = lg (k/T), ось ординат при lg ω = 0; L₂ = 20 lg (k/T). Прямые L₁ и L₂ пересекаются в точке сопряжения. Приравняв 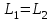, найдем частоту сопряжения: 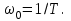(Ее также называют собственной частотой инерционного звена). Общий вид графика представлен на рис.3.2.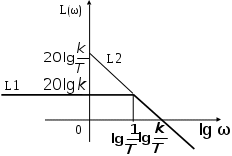

Рис. 3.2. Общий вид асимптот ЛАЧХ инерционного звена
Переходная функция находится как решение уравнения (3.3) при x = 1 и у(0) = 0:

.

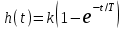h(t) возрастает экспоненциально и стремится стать равной k при  ∞.
П

ример 3.1.

Построить график комплексной частотной характеристики инерционного звена для k = 10, Т = 0,1.

Построение выполняется по формуле

,

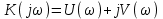где , .

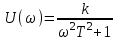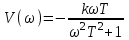Данные заносятся в таблицу 1.

Таблица 1

ω	ω2Т 2+1	U	V
∞ 0 10 3,16 31,6	∞2 1 2 1,1 11	0 10 5 9,1 0,91	0 0  5  2,9  2,9

---

Подставляя в формулы исходные данные, получаем:

,

.

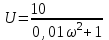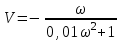Вначале находим координаты пересечения:

U = 0, ω = ∞, V(∞) = 0.

V = 0, ω = 0, U(0) = 0.

Затем задаем удобные для вычисления значения ω.

, , .

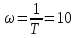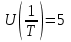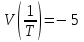ω = 3,16, (ω²  10), U(3,16) = 9,1, V(3,16) =  2,9.

ω = 31,6, (ω²  1000), U(31,6) = 0,91, V(31,6) =  2,9.

Полученных значений UиVдостаточно, чтобы приближенно провести контур кривой. Необходимые для уточнения хода кривой точки задаются по интуиции.

Кривая 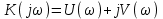вычерчивается на комплексной плоскости. По оси абсцисс откладываются значения U(ω), по оси V(ω). Вид графика комплексной частотной характеристики показан на рис. 3.3.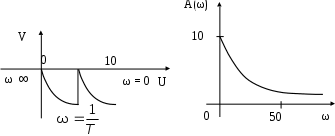

Рис. 3.3. График комплексной Рис. 3.4. Зависимость

частотной характеристики амплитуды от частоты





Пример 3.2.

Построить амплитудную частотную характеристику инерционного звена для k = 10, Т = 0,1.

Построение выполняется по формуле

.

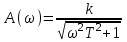С заданными значениями k и Т

.

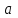Задавая ω = 0; 10; 20; 30; 50; ∞ соответственно получаем А = 10; 7; 4,5; 3,2; 2; 0.

График представлен на рис. 3.4.

3.4. Интегрирующее звено
Дифференциальное уравнение этого звена устанавливает пропорциональность скорости изменения выходной величины величине входного воздействия:

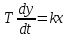(3.4)

(Сама выходная величина пропорциональна интегралу от входной величины,

.

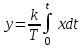Отсюда и название звена – «интегрирующее»).

Операторное уравнение:

.

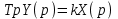Передаточная функция:

---

.

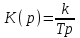
Комплексная частотная характеристика

.

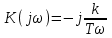Действительная частотная характеристика U(ω) = 0. Мнимая частотная характеристика V(ω) = – k/Tω.

Амплитудная частотная характеристика

.

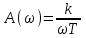При ω = 1/T, амплитуда равна коэффициенту усиления. В области ω < 1/T амплитуда возрастает по мере уменьшения ωи когда ω = 0, становиться равной ∞. В области ω > 1/T амплитуда уменьшается с увеличением ω и стремиться к нулю при неограниченном увеличении ω.

Фазовая частотная характеристика от ω не зависит:

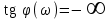, φ = – 90. Запаздывание по фазе постоянное при любой частоте.

Логарифмическая амплитудная частотная характеристика

.

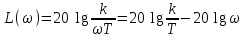В области низких частот ω 1 и в области высоких частот ω  1 вид функции один и тот же. Зависимость представляет собой прямую, которая пересекает ординату в точке с координатами lg ω = 0, L(ω) = 20 k/T и абсциссу в точке с координатами lg ω = lg (k/T), L(ω) = 0. Рис 3.5.

Логарифмическая фазовая частотная характеристика от частоты не зависит.

Переходная функция – прямая с уравнением

.


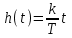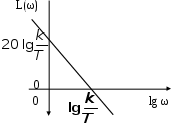
Рис. 3.5. Логарифмическая амплитудная частотная характеристика

интегрирующего звена
Характеристиками интегрирующего звена обладают так называемые интегральные регуляторы (сокращенно И - регуляторы). Их применение позволяет снизить ошибку регулирования.

3.5. Дифференцирующее звено
Сначала рассмотрим идеальное дифференцирующее звено. Дифференциальное уравнение этого звена устанавливает пропорциональность выходной величины скорости изменения входной величины:

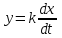. (3.5)

Операторное уравнение: Y(p) = kpX(p).

Передаточная функция



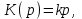
где k – коэффициент, имеющий размерность времени.

Комплексная частотная характеристика

.

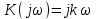Действительная часть U(ω) = 0, мнимая часть V(ω) = k ω.

---

Амплитудная частотная характеристика

.

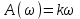Амплитуда растет линейно с частотой.

Фазовый угол для всех частот 90, что означает постоянное опережение по фазе при любой частоте.

Переходная функция – в ответ на единичное ступенчатое воздействие – имеет вид:



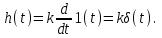
То есть, на выходе появляется единичный импульс, усиленный в k раз.

Осуществить практически идеальное дифференцирующее звено невозможно. Но реализуемы математические модели, в которых присутствует дифференцирующая составляющая dx/dt. Так, если записать в правой части инерционного звена вместо усилительного дифференцирующее воздействие, получается математическая модель, которую называют «реальное дифференцирующее звено».

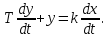(3.6)

Операторное уравнение: (Tp + 1)Y(p) = kpX(p).

Передаточная функция

.

---
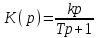