Файл: Руководство по выполнению базовых экспериментов эцпет. 001 Рбэ (902) 2006.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 614
Скачиваний: 1
СОДЕРЖАНИЕ
2. Параметры синусоидального напряжения (тока)
3. Активная мощность цепи синусоидального тока
4. Цепи синусоидального тока с конденсаторами
4.1. Напряжение и ток конденсатора
4.2. Реактивное сопротивление конденсатора
4.3. Последовательное соединение конденсаторов
4.4. Параллельное соединение конденсаторов
4.5. Реактивная мощность конденсатора
5. Цепи синусоидального с катушками индуктивности
5.1. Напряжение и ток катушки индуктивности
5.2. Реактивное сопротивление катушки индуктивности
5.3. Последовательное соединение катушек индуктивности
5.4. Параллельное соединение катушек индуктивности
5.5. Реактивная мощность катушки индуктивности
6. Цепи синусоидального тока с резисторами, конденсаторами и катушками индуктивности
6.2. Параллельное соединение резистора и конденсатора
6.3. Последовательное соединение резистора и катушки индуктивности
6.4. Параллельное соединение резистора и катушки индуктивности
6.6. Параллельное соединение конденсатора и катушки индуктивности.Понятие о резонансе токов
6.7. Частотные характеристикипоследовательного резонансного контура
6.8. Частотные характеристики параллельного резонансного контура
6.9. Мощности в цепи синусоидального тока
7.2. Коэффициент трансформации
7.4. Определение параметров схемы замещения и построение векторной диаграммы трансформатора
7.5. Внешняя характеристика и коэффициент полезного действия (КПД) трансформатора
8. Трехфазные цепи синусоидального тока
8.1. Напряжения в трехфазной цепи
8.2. Трехфазная нагрузка, соединенная по схеме «звезда»
8.3. Трехфазные нагрузки, соединенные по схеме «треугольник»
8.4. Аварийные режимы трёхфазной цепи при соединении нагрузки в звезду
8.5 Аварийные режимы трёхфазной цепи при соединении нагрузки в треугольник
9. Расчёт и экспериментальное исследование цепи при несинусоидальном приложенном напряжении
10. Переходные процессы в линейных электрических цепях
10.1. Переходный процесс в цепи с конденсатором и резисторами
10.2. Процессы включения и отключения цепи с катушкой индуктивности
Вычислите = arctg (UL R), Z = U I, XL = UL I, занесите результаты вычислений в табл. 6.3.1 и сравните с результатами виртуальных измерений, если они есть.
-
Выберите масштабы и постройте векторную диаграмму напряжений (рис. 6.3.5) и треугольник сопротивлений (рис. 6.3.6).


Рис. 6.3.5 Рис. 6.3.6
6.4. Параллельное соединение резистора и катушки индуктивности
6.4.1. Общие сведения
Когда к цепи (рис. 6.4.1) с параллельным соединением резистора и катушки подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.
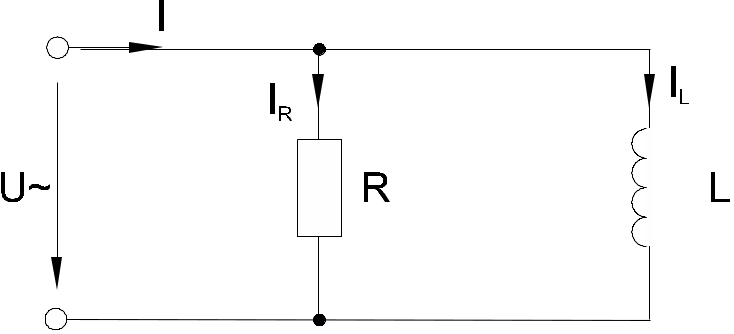
Рис. 6.4.1
Общий ток цепи I разветвляется на ток в катушке IL (индуктивная составляющая общего тока) и ток в резисторе IR (активная составляющая).
Между токами I, IL и IR существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлением XL катушки. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.4.2).
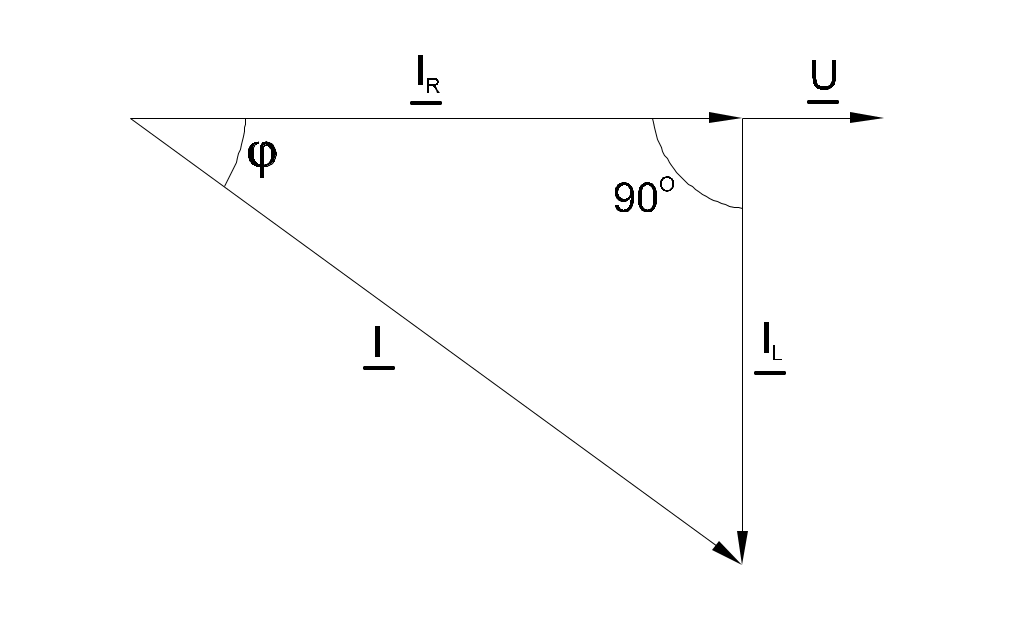 | 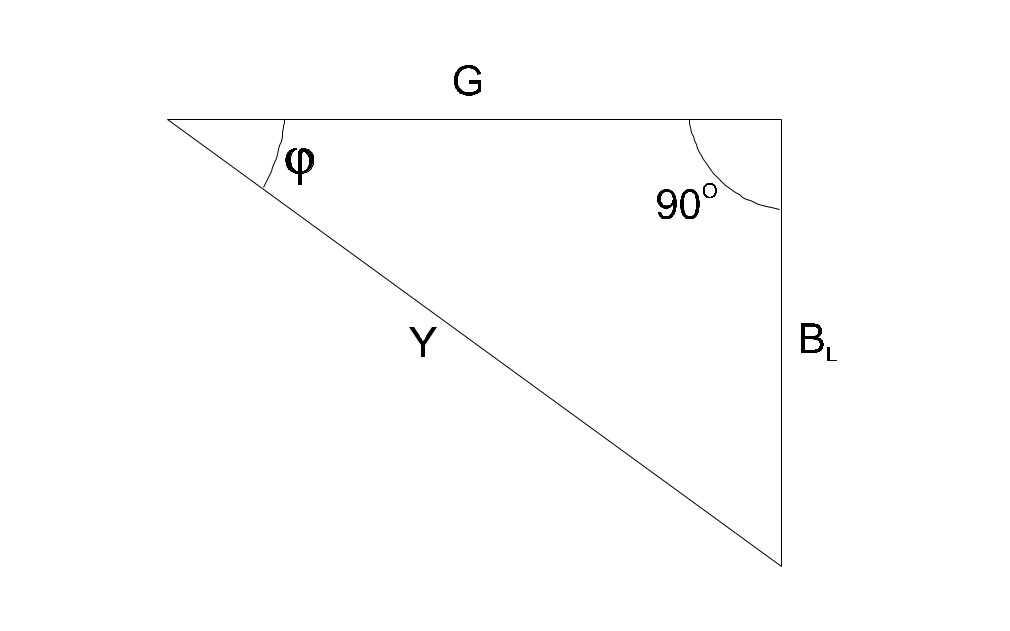 |
| Рис. 6.4.2 | Рис. 6.4.3 |
Фазовый сдвиг между напряжением U цепи и током в резисторе IR отсутствует, тогда как ток в катушке IL всегда отстает от напряжения цепи (или тока в резисторе IR) на 900. При этом сдвиг между полным током I и напряжением цепи U определяется соотношением между проводимостями BL и G.
Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.4.3), в котором Y представляет собой так называемую полную проводимость цепи, G – активную, а BL – реактивную (индуктивную) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных значений токов в параллельных ветвях, как в параллельной чисто резистивной цепи, невозможно. Только в векторной форме I = IR +IL. Расчет ведется по следующим формулам:
Действующее значение полного тока цепи
,
I = U Z = UY .
Полная проводимость цепи
Y = 1 Z ,
где Z - полное сопротивление цепи.
Угол сдвига фаз
= arctg (I L IR) = arctg (BL G).
Активное сопротивление цепи
G = Y cos \
Реактивное сопротивление цепи
B = Y sin .
6.4.2. Экспериментальная часть
Задание
Для цепи с параллельным соединением резистора и катушки индуктивности измерьте действующие значения тока в резисторе IR и катушке IL, полный ток I и вычислите угол сдвига фаз , полное сопротивление цепи Z и индуктивную реактивную проводимость BL.
Порядок выполнения работы
-
Соберите цепь согласно схеме (рис. 6.4.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
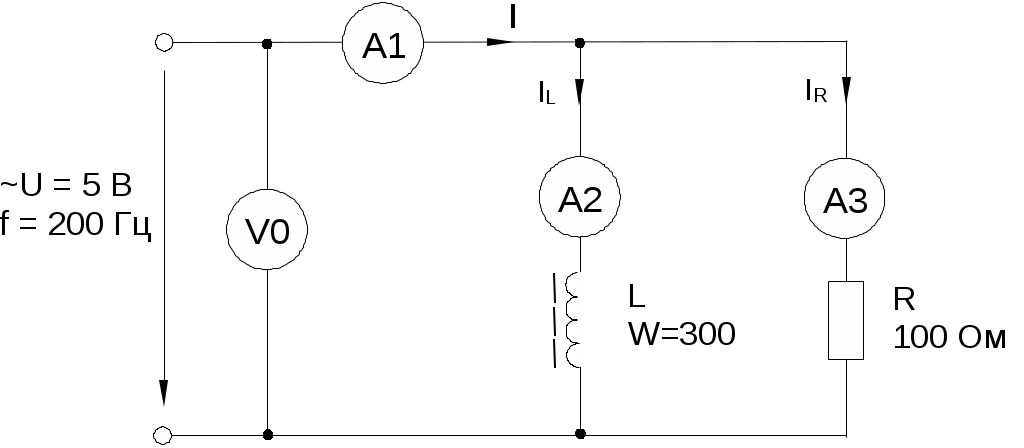
Рис. 6.4.4
-
Выполните измерения U, I, IL, IR и занесите результаты в табл. 6.4.1. Если измерения производятся виртуальными приборами, то измерьте также R, , XL, Z и вычислите G = 1/R, BL = 1/XL и Y = 1/Z. Занесите эти результаты в строку «виртуальные измерения» табл. 6.4.1.
Таблица 6.4.1.
-
U, B
I, мА
IL, мА
IR, мА
, град
G, 1/Ом
BL, 1/Ом
Y, 1/Ом
Примечание
Расчет
Вирт. изм
-
Вычислите = arctg (I L I R ); Y = I U; G = IR U ; BL = IL U. -
Занесите результаты вычислений в таблицу и сравните с результатами измерений виртуальными приборами, если они есть. -
Выберите масштаб и постройте векторную диаграмму токов (рис. 6.4.5) и треугольник проводимостей (рис. 6.4.6).


Рис. 6.4.5 Рис. 6.4.6
6.5. Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений
6.5.1. Общие сведения
Когда по цепи (рис. 6.5.1) с последовательным соединением конденсатора и катушки индуктивности протекает один и тот же синусоидальный ток I, напряжение на конденсаторе UC отстает от тока I на 900, а напряжение на катушке индуктивности UL опережает ток на 900. Эти напряжения находятся в противофазе (повернуты относительно друг друга на 1800).
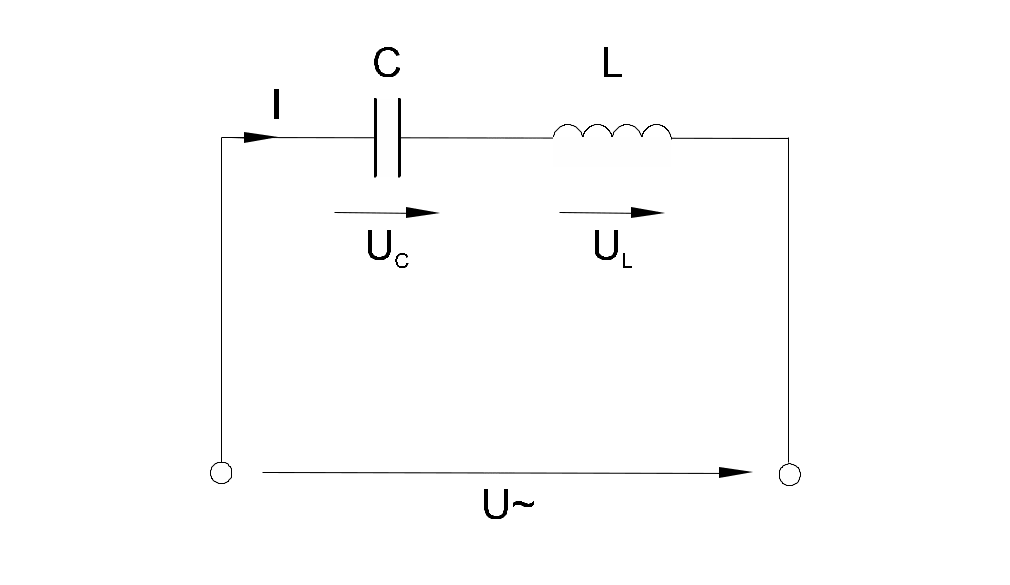
Рис. 6.5.1
Когда одно из напряжений больше другого, цепь оказывается либо преимущественно индуктивной (рис. 6.5.2), либо преимущественно емкостной (рис. 6.5.3). Если напряжения UL и UС имеют одинаковые значения и компенсируют друг друга, то суммарное напряжение на участке цепи L – C оказывается равным нулю. Остается только небольшая составляющая напряжения на активном сопротивлении катушки и проводов. Такое явление называется резонансом напряжений (рис. 6.5.4).
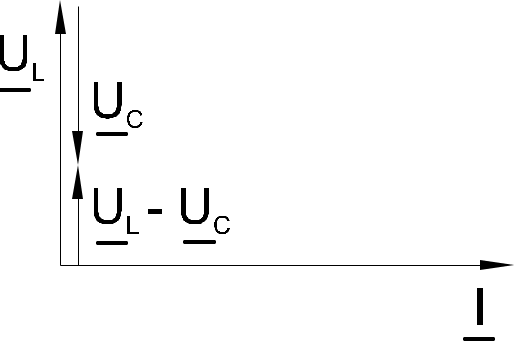 | 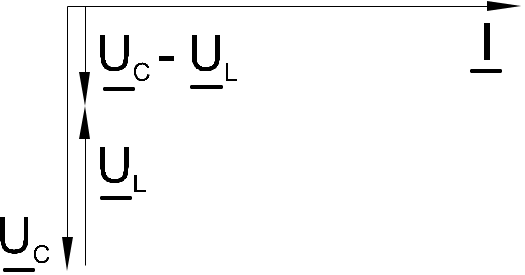 | 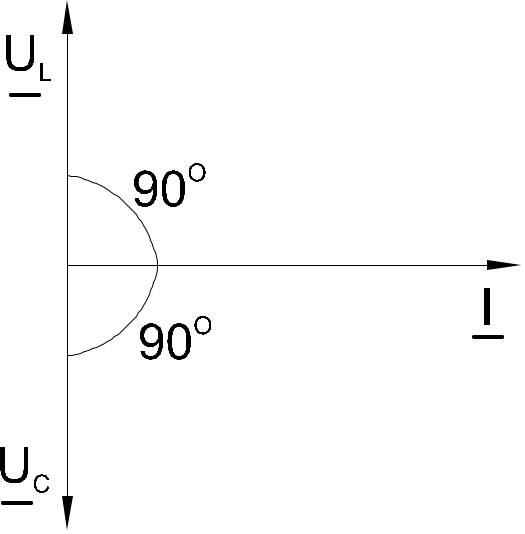 |
| Рис. 6.5.2 | Рис. 6.5.3 | Рис. 6.5.4 |
При резонансе напряжений реактивное сопротивление цепи
X = XL – XC
оказывается равным нулю. При заданных значениях L и C резонанс может быть получен путем изменения частоты.
Поскольку XL = L, а XC = 1 / C, то резонансная частота 0 может быть определена из уравнения:
0L – 1 / 0C = 0,
откуда
Полное сопротивление цепи при резонансе оказывается равным небольшому активному сопротивлению катушки